Как мы могли видеть, для работы с большими числами, простые операции сложение, умножение, деление и т. д. не применимы. Для этого существует специальный класс операций. Это операции, которые возвращают сумму, разность, субстрат, произведение multiply, devide частные и mod, остаток от деления одного числа на другое.

Также у больших чисел есть специальный оператор сравнения compare To, который сравнивает два числа и возвращает значение 0, если: данное число больше второго, возвращает отрицательное число, если данное число больше, и возвращает положительное число в противном случае.

Последний оператор, оператор valueOf, который возвращает большое число, значение которого равно переменной Х, превращая ее в большое число для наших дальнейших операций. Этот оператор мы уже использовали в нашей программе. Операции с большими числами возможны, конечно же, не только с целыми, но и с действительными числами, числами с плавающей запятой.

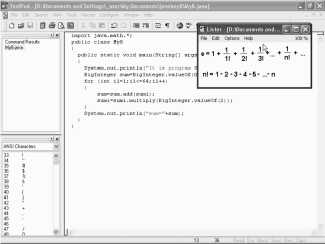
Для этих целей приведем пример. Например, подсчитаем число e с большой точностью. Для этого воспользуемся вот такой формулой для подсчета числа e. Е - это есть сумма обратных величин факториалов натуральных чисел. А число факториал, это произведение от 1 до n, всех натуральных чисел. Воспользуемся этой формулой. Поскольку возрастание n, это число очень быстро убывает, то эта формула достаточно быстро сходится. Для контроля выведем сначала число e, которое есть в этом пакете Math, на принтер. И, чтобы не писать, выделим эту часть текста. Правая кнопка мыши, Сору. Затем вставим сюда. Правая кнопка мыши, Paste.

И теперь напишем таким образом. Число E, знак равенства, кавычки, плюс и теперь его представление из пакета Math. Поэтому напишем Math, точка и далее большую букву Е. Закроем скобку, точка с запятой. Теперь попробуем это все подсчитать. Для этого введем переменную типа BigDecimal, которая и является действительным числом с большой точностью. Назначим число e и введем для него начальное значение.

Как мы помним, прямо присвоить какое-либо значение тут мы не можем. И, так же как и в случае с натуральными числами, нам нужно воспользоваться специальным оператором valueOf. Но, на этот раз возьмем не BigInteger, а BigDecimal, точка. Теперь valueOf. И в скобках присвоим ему значение 0, запятая. Теперь в отличие от целого числа, здесь мы можем указать вместе с его значением и точность количества цифр, с которой мы хотим это число иметь. Возьмем, например, число 35. Мы хотим узнать точность числа е 35 знаков. Далее закроем скобку, запятая.

И возьмем еще одно число. Обозначим его e1, в котором будем хранить число единица деленное на n факториал. Проинициализируем это число. Для этого скопируем вот этот кусок текста. Правая кнопка мыши, Сору. Далее вставим сюда. Правая кнопка, Paste. Точка с запятой. Вот теперь у нас две переменные, типа BigDecimal уже есть.

Единственное, во втором из этих чисел запишем теперь единицу для начала. Поэтому напишем таким образом, e1, знак равенства, далее e1, точка add (добавить), и добавим единицу. Но нам нужно воспользоваться вот этим оператором BigDecimal valueOf. Поэтому скопируем, выделим. Правая кнопка мыши, Сору. Вставим сюда. Правая кнопка, Paste. И добавим здесь, конечно же, единицу. Теперь нам точность не нужна, в e1 у нас точность уже зафиксирована, поэтому закроем все скобки и поставим точку с запятой.

Введем еще одну переменную, просто integer. Пусть это будет i1, которая нам понадобится для организации цикла. Для начала ее проинициализируем нулем, и далее напишем оператор цикла while. Условием у нас пусть будет точность, и для этого напишем такое выражение. Е1, прекращать мы будет вычисление, когда вот это число e1, у нас будет меньше, чем 10 минус в 35 степени, поскольку мы как раз и хотим взять 35 знаков.

Поэтому напишем таким образом, e1, далее оператор сравнения, compareTo. Как мы помним, простые операторы больше - меньше мы здесь использовать не можем, поэтому напишем compareTo, и скобки, внутри которых нам опять надо воспользоваться вот этой конструкцией BigDecimal valueOf.

Поэтому выделим. Правая кнопка мыши, Сору. Вставим сюда. Правая кнопка мыши, Paste. Точка с запятой нам не нужна, и вместо нуля напишем единицу. И тогда, вот это число, будет числом 1 умноженное на 10 в минус 35 степени. Закроем теперь еще одну скобку и далее, как мы помним, точно так же как и в случае с целыми числами, вот этот оператор compareTo выдает нам значение 0, если эти два числа равны, а значение больше 0 или меньше 0, в зависимости от того, какой из этих чисел больше. Поэтому возьмем больше или равно 0. Пока это верно, вычисления у нас будут происходить. Внутри фигурных скобок нам нужно написать, что же у нас будет происходить, так сказать, в теле цикла.

Увеличим значение i1 на единицу, i1++. Точка с запятой. Далее, к значению e надо добавить значение e1. Для этого опять воспользуемся оператором e, точка add, добавить. Далее скобки и значение, которое у нас есть в переменной e1. Закроем скобку, точка с запятой. Теперь нужно e1 разделить на n, для того чтобы там все время сохранялось число 1 деленное на n факториал. Поэтому напишем e1, знак равенства e1, точка и далее divide (делить), скобка. Теперь нам понадобится опять вот эта функция, преобразование обычных чисел в большое число. Выделим. Правая кнопка мыши, Сору. Вставим сюда. Правая кнопка мыши, Paste. Делить нам, конечно же, нужно на вот это число e1, на переменную нашего цикла i1.

Закроем скобку, запятая. И теперь нам нужно указать, как будет происходить округление при нашей операции деления. Напишем таким образом, BigDecimal, точка. И далее режим округления Round Half Up, который означает обычное округление. Т.е. если последняя цифра меньше 5, то остальные цифры отбрасываются, и если следующая цифра больше или равна 5, последняя цифра увеличивается на единицу.

Далее закроем скобки, точка с запятой. Следующим оператором выведем все это на печать. Для этого воспользуемся операцией println. Скопируем. Правая кнопка мыши, Сору. Вставим сюда. Правая кнопка, Paste. Далее выведем на печать оба числа, и единицу делить на n факториал, т.е. число е1 и само число е, подсчитанное нами.

Для этого напишем el, плюс. Введем еще пару пробелом между этими двумя числами, чтобы они отделялись друг от друга и далее само число е, которое напишем таким образом, е, закроем скобку, точка с запятой. В принципе, мы можем ввести и такой символ е со знаком равенства, чтобы это все у нас было видно более четко, что у нас тут происходит. Теперь скомпилируем эту программу и запустим ее на выполнение. Для этого Tools, Compile Java. Далее Tolls, Run Java Application. И вот можно видеть, что у нас получилось. Немножко растянем это окно, для того чтобы у нас все наши вычисления поместились и можем видеть, как у нас изменялось число е при вычислениях. И как у нас изменялся обратный факториал.

Как мы видим, он у нас все время мешался, пока не дошел до 0. А число е у нас получилось вот такое. Как мы видим, оно в принципе достаточно точно совпадает с числом е, которое у нас находилось в пакете Math. Первое, соответствующее количество цифр у нас совпадает, а далее после этого, мы дополнительно подсчитали еще достаточно много количества цифр.

Надо сказать, что, скорее всего, последняя цифры l или 2, тут вряд ли будет правильными из ошибок округления, но где-то 34, 33 цифры здесь будут абсолютно верными. Вот таким образом мы подсчитали число е. Конечно же, такие вычисления при помощи обычных операций сложения, вычитания и т. д. с обычными целыми действительными числами, даже с двойной точностью недоступны. Закроем теперь это окно. И вернемся в наш обычный редактор.

⇐Большие числа. арифметические операции | TeachPro WEB-дизайн | Одномерные массивы. создание. инициализация.⇒