Вероятностные характеристики идеального неполнодоступного включения при многоканальной коммутации и маркированной пуассоновской нагрузке Интеграция различных видов связи (телеграфной, телефонной, передачи данных и др.) на основе единых организационных и технологических принципов является одним из этапов создания ЦСИС. На таких сетях абонентам будет предоставлена возможность передавать различную по виду и объему информацию в цифровом виде. Системы коммутации ЦСИС при обслуживании вызова в зависимости от вида информации должны соединять между собой одновременно / каналов (1 < / < V, где V- число каналов в направлении связи).

При исследовании вероятностных характеристик КС часто используют модель идеального неполнодоступного включения (ИНПД) [4.1, 4.8-4.10, 4.12], например, в [4.8] для расчета многозвенных КС при /'=1,2.

Рассмотрим более общий случай ИНПД, при / < V, т. е. случай, отвечающий требованиям ЦСИС, и выведем формулы для расчета вероятностных характеристик КС, соответствующих данной модели [4.2].

Пусть на систему с ИНПД с V каналами, характеризующуюся доступностью с1, поступает стационарный пуассоновский поток вызовов с параметром А. С вероятностью со, = А,,. / А, / = 1, и, и < с/ поступает вызов, требующий для обслуживания / каналов, / = 1, и. Назовем такой вызов 1-канальным. Если число свободных каналов в момент поступления 1-канального вызова меньше г, то этот вызов теряется. Длительность обслуживания 1-канальных вызовов подчинена экспоненциальному закону с параметром г;. Нагрузку, создаваемую 1-канальными вызовами, в дальнейшем будем называть маркированной, так как каждому поступающему вызову приписывается некоторое число (марка), характеризующее число каналов, необходимое для обслуживания этого вызова.

Действие такой системы можно описать маркированным марковским процессом *_и, где х,- - число 1-канальных вызовов, об служиваемых системой в момент /. Обозначим множество состояний этого процесса

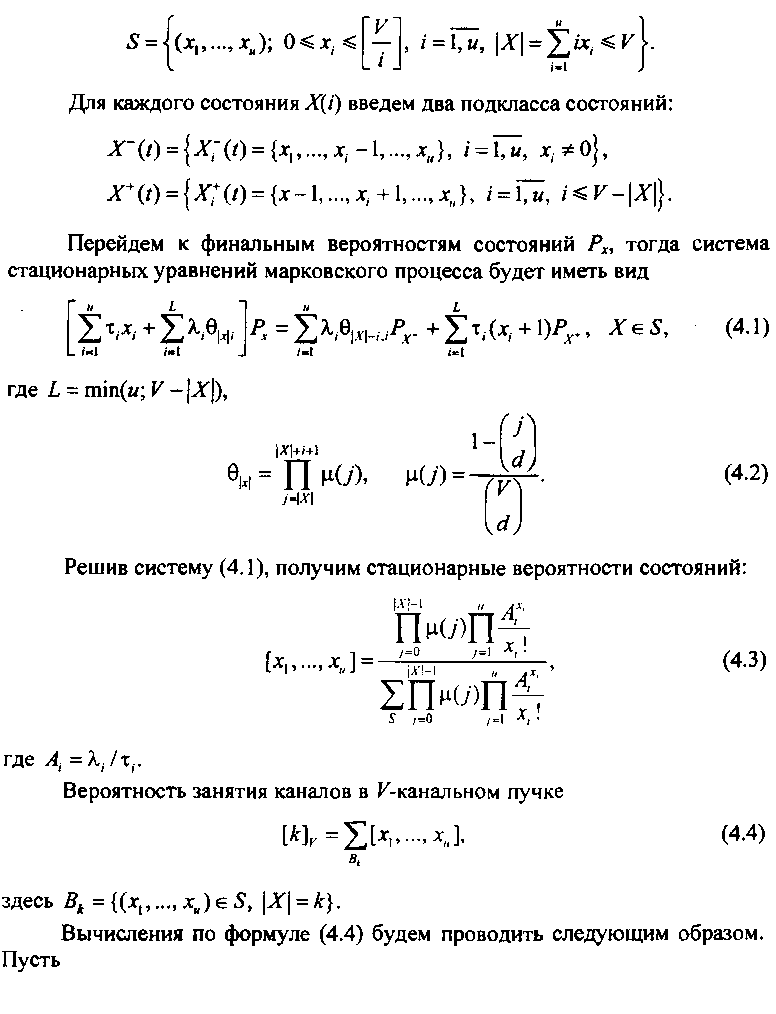
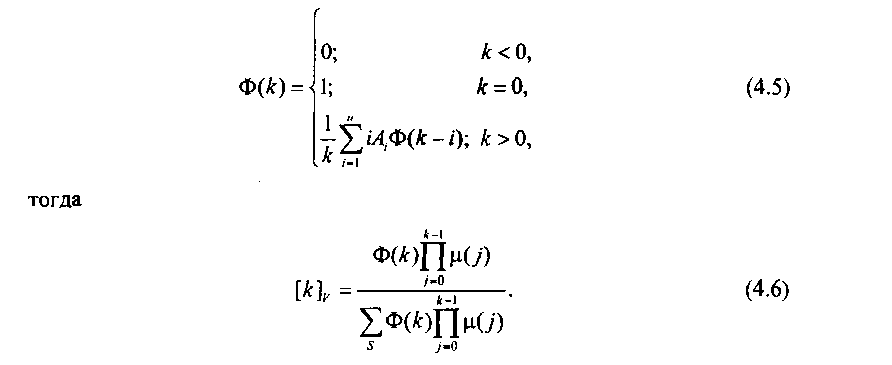
Потери 1-канальных вызовов происходят в случае, когда \Х\ + / > V. Если обозначить потери 1-канальных вызовов из-за занятости каналов пучка через Руи то

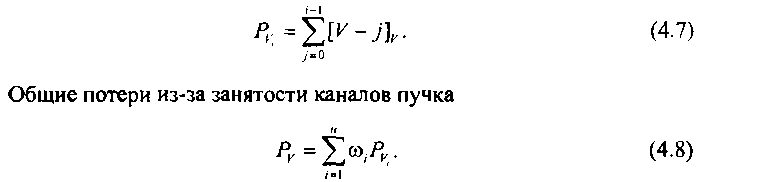
Запишем выражение для вероятности потерь вызовов из-за внутренних блокировок модели ИНПД, работающей в режиме группового искания (ГИ). При наличии / свободных каналов в пучке может оказаться, что каждый из этих каналов заблокирован. Вероятность блокировки одного из каналов зависит от успешного установления остальных соединений. С учетом этих соображений выведем выражение вероятности блокировки при установлении соединения для 1-канального вызова в режиме ГИ:

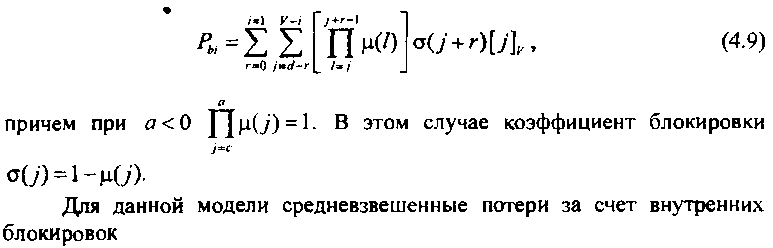
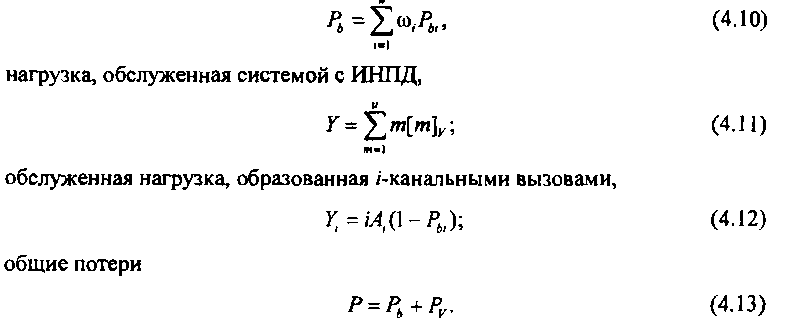
Полученные формулы для расчета вероятностных характеристик модели ИНПД при обслуживании неординарного потока вызовов весьма сложны, поэтому был проведен их численный анализ. На рис. 4.1 представлены зависимости вероятностей Рщ, Р_ы(/ = 1,2,4, 8), Р, Р_уи Р_ьот изменения емкости

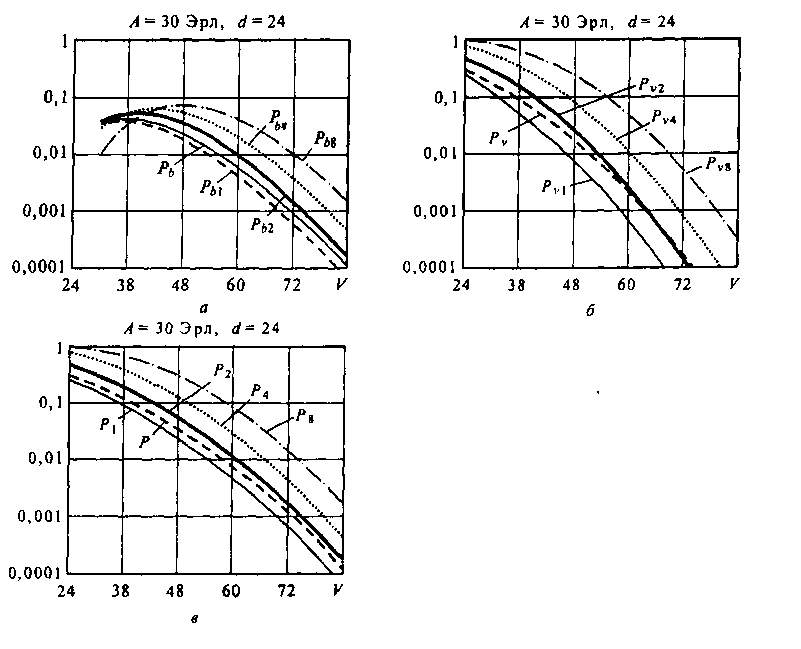
Рис. 4.1. Зависимость вероятностей Р, Ру, Ры Рщ и Ры от изменения емкости пучка каналов при фиксированной нагрузке и доступности пучка каналов V при фиксированной интенсивности поступающей нагрузки и А = 2] 4 =30 Эрл и доступности с! = 24. Анализ этих кривых показывает,

/=*1

что с увеличением емкости пучка каналов общая вероятность потерь Р и вероятность потерь из-за занятости каналов пучка /V падают. Сказанное относится и к вероятностям Рщ. Зависимости Р_ы(У) характеризуются наличием максимумов при некоторых значениях V.

На рис. 4.2, а-в представлены зависимости вероятностей Р, Ру, Р_ь, Р„, Ры от изменения интенсивности поступающей нагрузки А при фиксированной емкости пучка каналов V = 30 и доступности с/ = 24. Анализ этих кривых показывает, что с ростом интенсивности поступающей нагрузки общая вероятность потерь Р и вероятности потерь 1-канальных вызовов из-за занятости пучка Рщ растут. На том же отрезке изменения А повышаются и Рь и Р_Ь\. Зависимости же вероятностей Р_ь2, Ры, и Ры характеризуются наличием максимумов, которые достигаются при некоторых значениях А.

Рис, 4.2. Зависимость вероятностей Р, Ру, Ры Рт и Ры от изменения нафузки при фиксированной емкости пучка и доступности

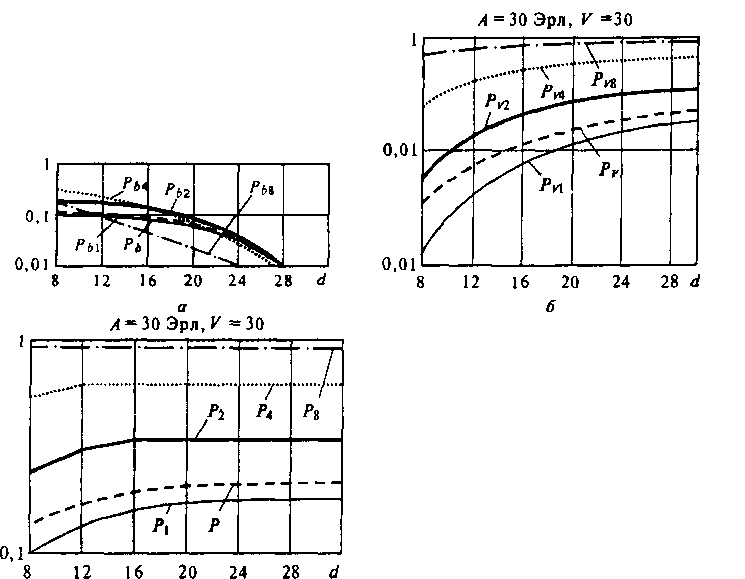
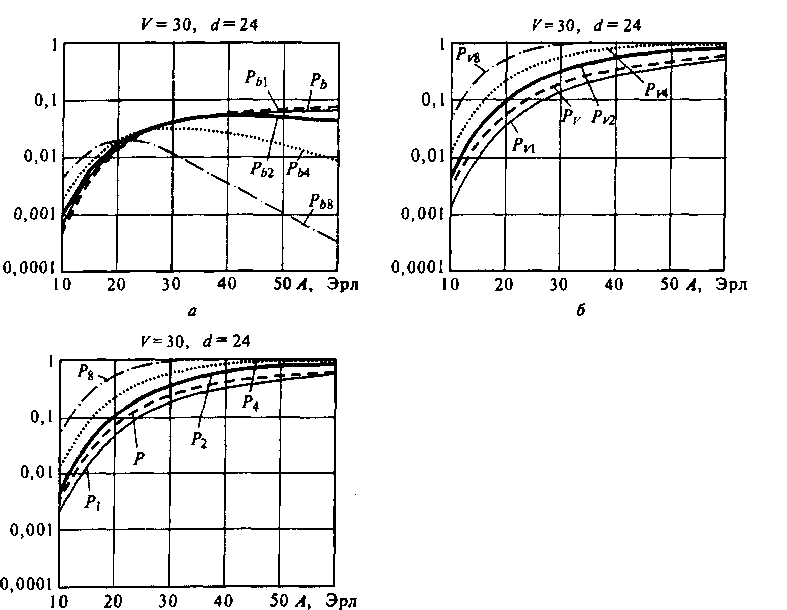
Рис. 4.3. Зависимость вероятностей Р, РV, Рь, Ру, и Ры от изменения доступности с! при фиксированных значениях пучка каналов и интенсивности поступающей нагрузки На рис. 4.3, а-в представлены зависимости вероятностей Р, Р„ Рь, Р_тРы от изменения доступности с1 при фиксированных значениях пучка каналов и интенсивности поступающей нагрузки А - 30 Эрл. Как видно из рисунка, с ростом доступности й! вероятности потерь 1-канальных вызовов из-за занятости каналов пучка растут, а общие потери Р и потери из-за внутренних блокировок падают.

Все представленные кривые построены при следующем соотношении интенсивностей поступающих нагрузок 1-канальных вызовов: А\. Ау. А*. А% = = 90 : 5 : 3 : 2.

Рассмотренную модель ИНПД можно использовать для приближенного описания вероятностных характеристик КС, предназначенных для работы на ЦСИС. Возможность использования этой модели для создания таких КС требует дальнейшего изучения. Численное исследование предложенной модели показало, что даже сравнительно небольшая доля вызовов, требующих для обслуживания более одного канала, вызывает весьма существенное уменьшение пропускной способности системы. Поэтому при разработке КС для ЦСИС весьма важной становится задача выбора оптимальной структуры и загрузки данной КС.

⇐Коэффициент доступности кс и его свойства | Мультисервисные телекоммуникационные сети | Вероятностные характеристики идеального неполнодоступного включения при многоканальной коммутации и маркированной нагрузке при конечном числе источников⇒