Вероятностные характеристики коммутационных систем с заявками, требующими одно- и двухканального ресурса с резервированием каналов Узкополосные цифровые сети интегрального обслуживания предполагают обслуживание абонентов, которым нужно обеспечить необходимую скорость передачи информации различного канального ресурса (КР), например, телефон и высокоскоростная передача данных. При поступлении на УК У-ЦСИС разноскоростного трафика потери для различных источников нагрузки, возникающие на УК, могут сильно различаться между собой. Для их выравнивания и обеспечения заданных норм потерь применяют различные методы. Один из таких методов состоит в пороговом ограничении доступа к канальному ресурсу определенного класса пользователей. Механизм ограничения доступа к канальным ресурсам называется резервированием канальных ресурсов (Trunk Reservation) и понимается как «бронирование ресурсов». Важным достоинством такого подхода является возможность управления качеством обслуживания на программном уровне. В настоящее время резервирование канальных ресурсов (РКР) является основным методом, используемым для управления качеством обслуживания. Идея РКР, возникшая при создании У-ЦСИС, нашла также широкое применение и при построении Ш-ЦСИС.
Как будет показано ниже, РКР является простым и при этом экстремально эффективным механизмом управления качеством обслуживания пользователей ТС.
Рассмотрим метод расчета вероятностных характеристик УК У-ЦСИС при неординарной пуассоновской нагрузке и пороговом ограничении канального ресурса.
Пусть на КС ЦСИС поступает нагрузка от двух типов источников [5.1, 5.15], причем один создает нагрузку А \ = \\l\i\, создаваемую вызовами, требующими для своего обслуживания одного канала в направлении связи (од-ноканапьные), а второй - нагрузку А2= Х,2/ц2, создаваемую вызовами, требующими для своего обслуживания двух каналов (двухканальные). При этом Х\ и Л2- интенсивности соответственно первого и второго потока вызовов, а Ц и ц2- соответствующие интенсивности обслуживания. Предполагается, что потоки вызовов являются пуассоновскими, а обслуживание вызовов подчиняется экспоненциальному закону.
Результирующая нагрузка А = А\ + А2, создаваемая этими источниками, является также пуассоновской и, так как занятие каналов при обслуживании заявки в системе происходит в зависимости от ее типа, а именно - либо одного, либо двух каналов одновременно, то такая нагрузка является неординарной. При этих предположениях система может быть описана марковским случайным процессом:
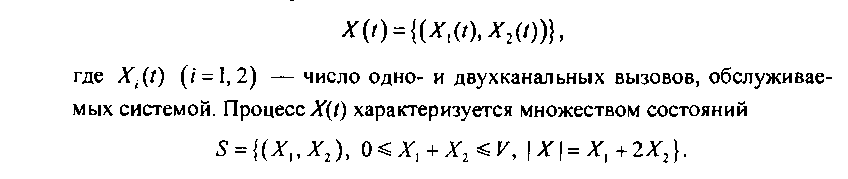
Предположим, что вызовы, требующие одноканального ресурса, имеют более низкий приоритет в обслуживании, чем вызовы, требующие двух-канапьного ресурса.
Присвоим вызовам, требующим одноканального ресурса, приоритет один, а вызовам, требующим двух каналов для обслуживания, приоритет два. Приоритеты упорядочены по номерам - чем больше номер, тем выше приоритет заявки.
Рассмотрим случай, когда дисциплина обслуживания вызовов первого приоритета такова, что предполагается ограничение доступа к канальному ресурсу путем введения порога Т, который равен числу каналов, используемых для обслуживания вызовов первого приоритета. При этом для вызовов другого приоритета остаются доступными для обслуживания все каналы.
На рис. 5.1 приведен граф переходов марковского случайного процесса при Т - V, где У- число каналов в направлении связи. Введение порога Т < V иллюстрируют диаграммы состояний (рис. 5.2). На рис. 5.2, а приведена диаграмма состояний для системы, имеющей общий ресурс У = 10 каПоступление двухканального Поступление одноканального вызова в состоянии X вызова в состоянии Х+ 1
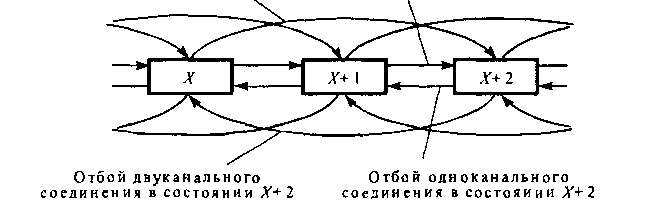
Рис. 5.1. Граф переходов для марковского случайного процесса при Т = V
налов и Т= 10, а на рис. 5.2, б - диаграмма состояний с У = 10 и Т= 9. Диаграмма состояний отражает переходы из состояния {г} в состояние {г + 1} при обслуживании одноканальрых заявок (ось ординат) и в состояние {/ + 2} при обслуживании двухканальных заявок (ось абсцисс).
Уравнения состояния системы уравнений равновесия марковского случайного процесса для стационарного режима с пороговым ограничением имеют вид
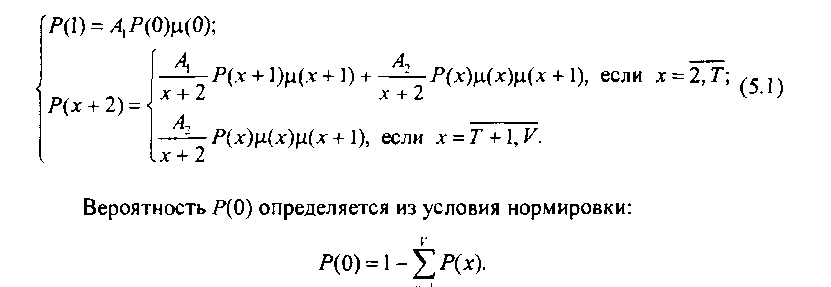
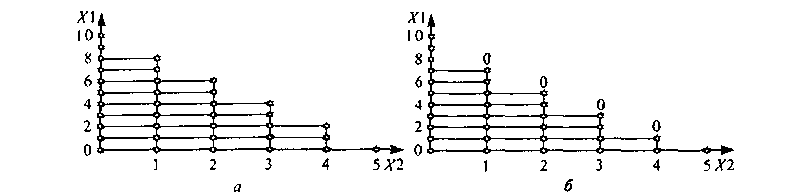
Рис. 5.2. Диаграмма состояний марковского случайного процесса: п - достижимое состояние; 0 - недостижимое состояние; а - Т = = 10, У= 10; б- Т= 9, У= 10
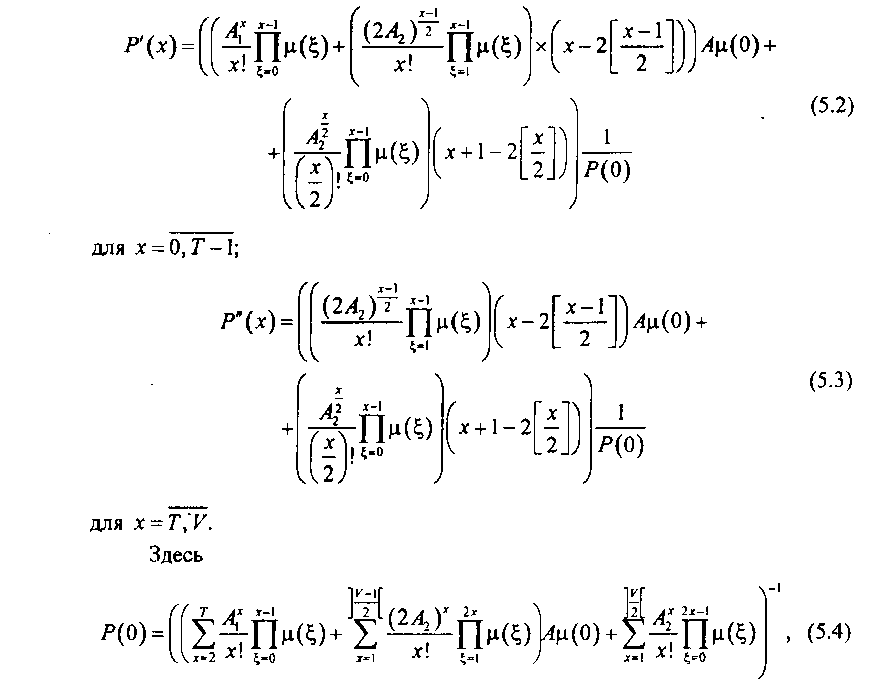
где Р'{х) - вероятность пребывания системы в состоянии {*} до порога Т; Р"(х) - вероятность пребывания системы в состоянии {*} после порога Т; А \ - нагрузка, создаваемая источником вызовов, требующих однократного канального ресурса; А2- нагрузка, создаваемая источником вызовов, требующих двукратного канального ресурса; ц(£) =1 - ст(£,); Т- порог; ст(£,) - вероятность внутренней блокировки вызова в состоянии (£,); V- число каналов КС; [х] - округление числа в большую сторону; ]х[ - округление числа в меньшую сторону.
С помощью формул (5.2)-(5.4) можно определить вероятность индивидуальных потерь вызовов из-за занятости канала и внутренней блокировки для заявок соответствующего приоритета. Для первого приоритета она будет определяться как сумма двух слагаемых, одно из которых будет учи-
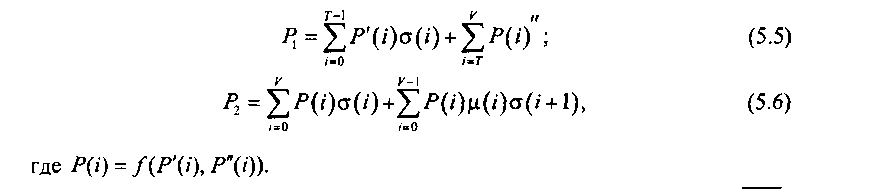
В правом слагаемом выражения (5.5) значение а{;} =1, для * = Г, V. Это учитывает то, что после порога Т все вызовы первого приоритета будут теряться. Для вызовов второго приоритета (5.6) учет а{;} в левом слагаемом проводится аналогично (5.5), но, так как этим вызовам предоставляется весь ресурс, то суммирование проводится до V. Второе слагаемое суммы учитывает вероятность того, что в состоянии {/} система будет свободна, но в следующем состоянии она окажется занятой.
Средневзвешенные вероятности потерь каждого типа трафика вычисляют по следующим соотношениям:

Если КС представляет собой ИНПД, то вероятность блокировки вызовов ст{£,} в состоянии {£,} определяют по формуле
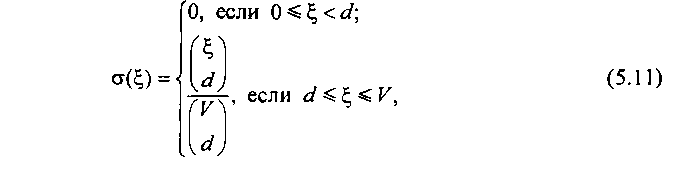
что совпадает с выражением, приведенным в [5.7], где <1 - доступность ИНПД.
Рассмотренный метод расчета можно использовать и для оценки вероятностных характеристик многозвенных систем коммутации, если доступность <3, входящую в а {с,}, определяемую согласно (5.1), интерпретировать как эффективную доступность этой системы. В этом случае соотношения (5.5)-(5.9) будут справедливыми и для ИНПД, которое широко используют для аппроксимации потерь в системах коммутации, характеризующихся сложной структурой.
Если ст{^} интерпретировать в терминах надежности, например, как вероятность повреждения оборудования в состоянии {£,}, то рассмотренная модель позволяет оценивать вероятность потерь вызовов в КС с пороговым огранйчением ресурса и ненадежными обслуживающими приборами.
Результаты анализа системы коммутации с ограниченной доступностью и резервированием каналов Рассмотрим в качестве примера систему коммутации с ограниченной доступностью со следующими параметрами: число каналов У= 30; коэффициент доступности ^ = -^- = 0,8 (эффективная доступность с1э= = 24); Т
относительный порог 0 =-, равный 0,9 и 1.
Предположим, что поступающая нагрузка А складывается из нагрузок А и А2, создаваемых соответствующими источниками, и соотношение инА\ . .
дивидуальных нагрузок у - - = 0,9.
А
Для этих условий был проведен численный анализ системы, результаты которого приведены на рис. 5.3 в виде графических зависимостей веро-
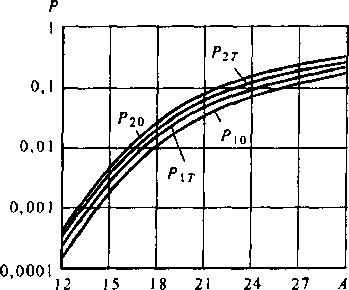
Рис. 5.3. Зависимость вероятностей потерь для одноканальных и двухка-нальных заявок при наличии порогового ограничения (Р1Т, Р2т) и без него (Р ю> Рг о): Р\о, Р-20 - индивидуальные вероятности потерь заявок 1 и 2 приоритетов соответственно для системы без порогового ограничения нагрузки (0= 1); Р1Т, Р2т- индивидуальные вероятности потерь заявок 1 и 2 приоритетов соответственно для системы с пороговым ограничением нагрузки (9=0,9)
ятностей потерь для заявок обоих типов от изменения интенсивности общей поступающей нагрузки А.
Как видно из графиков рис. 5.3, введение порогового ограничения приводит к существенному перераспределению вероятностей потерь вызовов для источников нагрузки различных категорий. В частности, введение порогового ограничения канального ресурса существенно уменьшает потери двухканапьных вызовов.
Выше были получены точные аналитические формулы вероятностей потерь заявок, требующих для своего обслуживания одно- и двухканапьно-го ресурса. Эти формулы можно применить для оценки вероятностных характеристик КС достаточно общего вида. Проведенное численное исследование метода показало, что предложенный метод расчета вероятностных характеристик УК ЦСИС с пороговым ограничением канального ресурса дает значительное снижение вероятности потерь приоритетных вызовов, тем самым выравнивая потери заявок обоих типов источников нагрузки и обеспечивая требуемый уровень качества обслуживания заявок.
Пусть коммутационное поле (КП) системы имеет емкость V» каналов в направлении связи (\у = 1,И, где И - число направлений связи) и доступность с!Лканалов.
Будем считать, что на каждое направление связи такой системы поступает стационарный разнородный пуассоновский поток вызовов, имеющий параметр Л*, образуемый в результате суперпозиции т неординарных пуассоновских потоков с интенсивностью X.,Л(г = 1, т), создаваемых различными типами источников нагрузки. Тогда вероятность поступления заявки 1-го типа будет характеризоваться значением
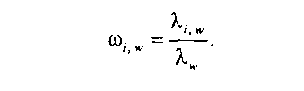
Кроме того, примем, что время обслуживания заявки 1-го типа подчинено экспоненциальному закону с параметром V,. В дальнейшем будем только рассматривать фиксированное направление связи и;. Поэтому для упрощения дальнейшего изложения индекс и>, когда это не вносит неясности, в формулах будем опускать.
Каждый тип источников нагрузки создает индивидуальный поток заявок, требующих для обслуживания одновременного занятия М, каналов в направлении связи (0 < М, < ф, и имеет ограничение предоставляемого канального ресурса путем введения порога Г, (0 < Г, < (1).
Предполагается, что при поступлении заявки 1-го типа происходит проверка следующих условий:
1) не превышает ли на момент поступления вызова общее число занятых каналов в направлении связи \Х\ в рассматриваемой КС значения порога 7};
2) существует ли М[ свободных каналов в требуемом пучке V КС для установления соединения;
3) возможно ли занятие М, промежуточных путей для М, каналов в пучке V.
Если хотя бы одно из этих условий не выполняется, заявка получает отказ в обслуживании.
Поведение системы, подчиняющейся этим правилам, можно описать уравнениями состояния марковского случайного процесса
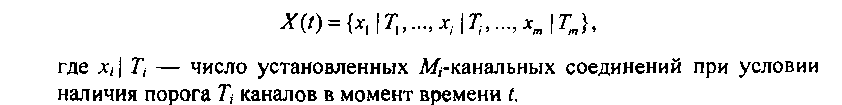
Множество состояний описываемого марковского процесса будет иметь вид
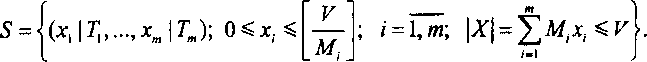
Определим два класса соседних состояний Х~ и X* для каждого состояния процесса Щ:
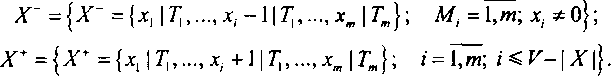
Запишем уравнения состояния марковского случайного процесса для стационарного режима
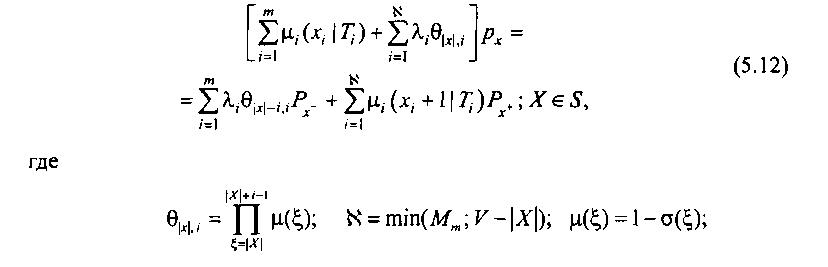
ст{^} - вероятность блокировки вызова из-за отсутствия свободных промежуточных путей в направлении искания и\
Решив систему уравнений (5.12), с учетом условия нормировки вероятностей пребывания в состояниях системы, можно найти стационарные вероятности состояний
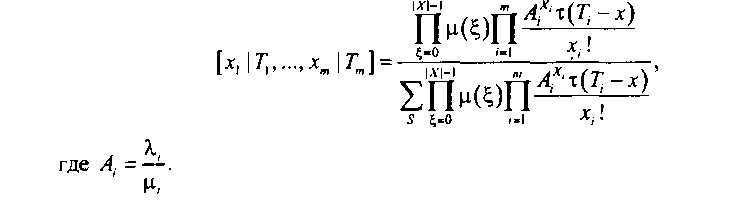
Вероятность занятия х каналов в пучке из V каналов при пороговом ограничении различных категорий заявок
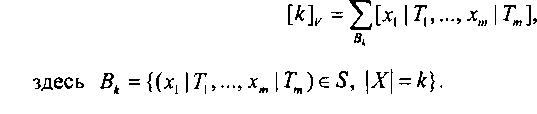
После преобразований выражение для вероятности пребывания в макросостоянии с х занятыми каналами имеет вид
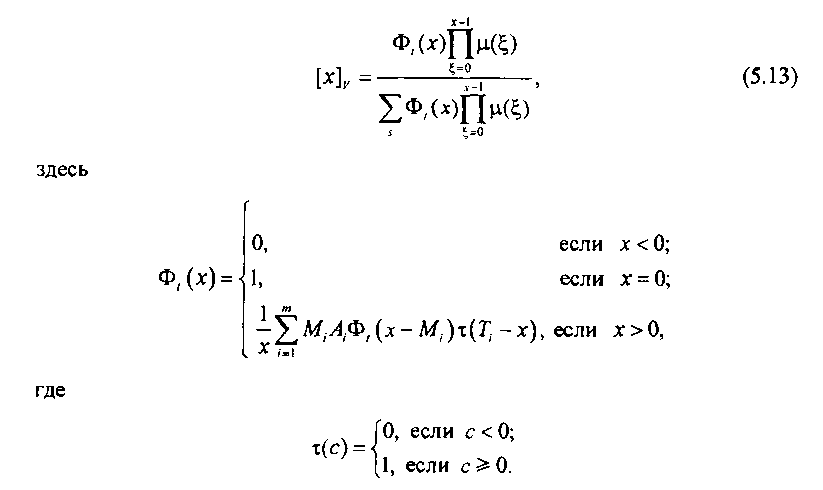
Значение функции х(с) учитывает наличие порога Г, при определении распределения вероятности числа занятых каналов в направлении связи. Потери М-канальных вызовов будут происходить, во-первых, если число занятых каналов в направлении связи х > 7), и во-вторых, если \Х\ + > V.
Обозначим вероятность потерь вызовов из-за занятости пучка Р„, а вероятность потерь вызовов из-за порогового ограничения и внутренних блокировок Рь. В этом случае вероятность потерь вызовов каждого типа трафика имеет вид
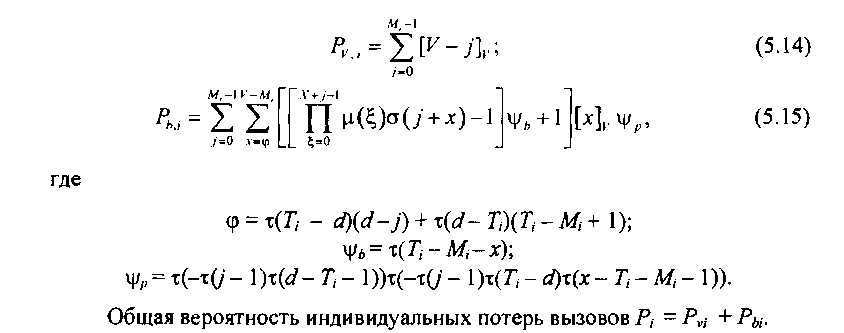
Средневзвешенные вероятности потерь каждого типа трафика из-за занятости пучка, внутренней блокировки и порогового ограничения вычисляют по следующим соотношениям:

Рассмотренный выше метод расчета при выполнении (5.21) можно ис пользовать и для оценки вероятностных характеристик многозвенных сис тем многоканальной коммутации с резервированием каналов, если доступ ность сі, входящую в о(^), интерпретировать как эффективную доступность а этой системы, определяемую согласно [5.9].
Если сг(^) интерпретировать в терминах надежности, например, каї вероятность повреждения оборудования в состоянии {%}, то рассмотренна) модель позволяет оценивать вероятность потерь вызовов в КС с пороговы\ ограничением ресурса и ненадежными обслуживающими приборами.
При расчете вероятностных характеристик систем многоканально? коммутации можно использовать следующий алгоритм вычисления вероят ностей потерь вызовов.
1. Задание исходных данных: К> Л*»М/.» ’=(і = 1, да).
2. Выбор начального значения коэффициента доступности:
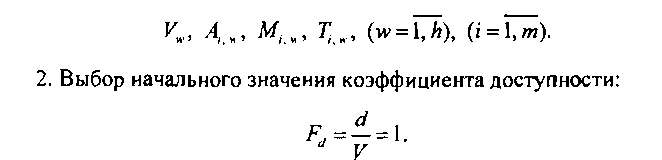
3. Расчет значений индивидуальных вероятностей и Р*и индивидуальных обслуженных нагрузок У по соотношениям (5.14)-(5.15).
4. Расчет общих средневзвешенных потерь и общей обслуженной нагрузки.
5. Вычисление нового значения коэффициента доступности и сравнение его с Рл6. Вычисление относительной погрешности а:
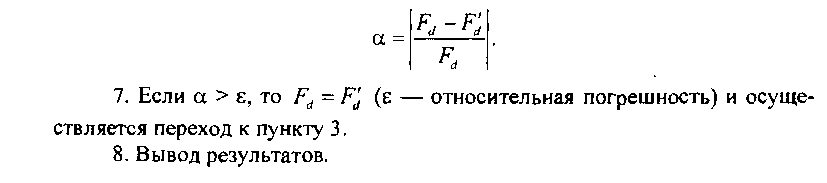
7. Если а > е, то (е - относительная погрешность) и осуществляется переход к пункту 3.
8. Вывод результатов.
Анализ трафика многозвенной системы коммутации с резервированием каналов Рассмотрим использование предложенного метода расчета вероятностей потерь вызовов в КС с пороговым ограничением каналов для тра-фичного анализа гипотетической системы коммутации. Пусть емкость пучка каналов в направлении связи V = 512 каналов и коэффициент доступности /\у = 0,8. Предположим, что есть четыре вида источников нагрузки, которым для обслуживания поступающего вызова необходимо следующее число каналов: 1, 2, 6, 30. Индивидуальные интенсивности поступающих нагрузок соотносятся между собой, как А\ : Л2: А3: А< = 80 : 7 : 3 : 10. Общая поступающая нагрузка А = 100 Эрл. Эффект введения порогового ограничения иллюстрируют результаты расчетов, приведенные в табл. 5.1 и 5.2. В табл. 5.1 приведены вероятностные характеристики рассматриваемой системы при отсутствии пороговых ограничений, т. е. когда 0 = 02= 0з - 04=1 (где 0, = Г, IV), а в табл. 5.2 - данные этой же системы, но для других коэффициентов относительного порога 0: 01 = 0,943; 02= 0,945; 03= 0,953; 04= 1. В этих таблицах Р - это средневзвешенная вероятность. Из сравнения вероятностных характеристик, приведенных в табл. 5.1 и 5.2, видно, что в первом случае имеет место значительный разброс потерь между всеми видами трафика. Так, например, отношение максимальных потерь к минимальным Р4
для первого случая равно = 36. При введении пороговых ограничений на определенные категории источников нагрузки достигается выравнивание потерь за счет незначительного уменьшения величины общей обслуженной нагрузки (около 0,5 %, т. е. отношение общих обслуженных нагрузок у ку.= -р-« 0,99, где У - нагрузка системы без порогового ограничения, а УТ- нагрузка системы при введении порогового ограничения).
Таблица 5.1
|
т |
А, % |
Марка заявки |
0 |
Р |
У |
|
1 |
80 |
1 |
1 |
0,0025 |
79,80 |
|
2 |
7 |
2 |
1 |
0,0051 |
13,93 |
|
3 |
3 |
6 |
1 |
0,0158 |
17,72 |
|
4 |
10 |
30 |
1 |
0,0899 |
273,03 |
|
Всего |
100 |
Р = 0,0119 |
384,47 |
||
Таблица 5.2
|
1 т |
А, % |
Марка заявки |
0 |
Р |
У |
|
1 |
80 |
1 |
0,943 |
0,0713 |
74,29 |
|
2 |
7 |
2 |
0,945 |
0,0713 |
13,00 |
|
3 |
3 |
6 |
0,953 |
0,0713 |
16,72 |
|
4 |
10 |
30 |
1 |
0,0724 |
278,29 |
|
Всего |
100 |
Р = 0,0714 |
382,30 |
Выше были получены аналитические формулы вероятностных характеристик системы коммутации при заявках, требующих для своего обслуживания ресурса, использующего разное число каналов и резервирования каналов в направлении связи определенных типов источников нагрузки. Метод можно использовать для оценки вероятностных характеристик КС достаточно общего вида (различное число каскадов, связность, размер коммутаторов и т. д.).
Проведенное численное исследование показало, что предложенный метод дает выравнивание вероятностей потерь вызовов в многозвенных КС, позволяя обеспечивать требуемый уровень качества обслуживания вызовов при незначительном снижении величины общей обслуженной нагрузки.
5.2.2. Пример применения математической модели РКР для анализа вероятностей потерь вызовов для двух классов пользователей - телефонного и мультимедийной связи Проиллюстрируем применение рассмотренной выше математической модели резервирования канальных ресурсов в ЦСИС на примере блокируемого пучка каналов, на который поступают нагрузки двух классов пользователей:
• нагрузка одноканальная - телефонные пользователи;
• нагрузка шестиканальная - мультимедийная связь.
Для того чтобы отчетливо проявить влияние внутренних блокировок, выберем двухкаскадную КС, в которой ее величина относительно велика. В качестве такой КС исследуем систему, имеющую следующую структуру:
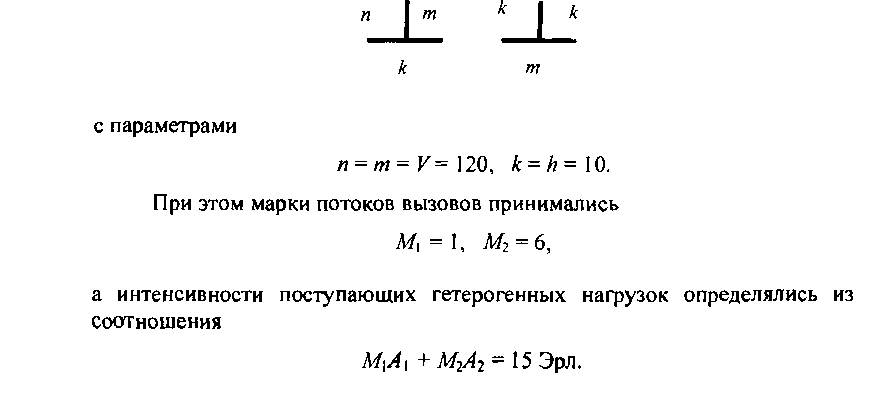
![Зависимость индивидуальных потерь Р одноканальных пользователей от изменения доли нагрузки шестиканальных пользователей и относительного порога 0]](/images/multiservisnue_telekommynikacionnue_seti/multiservisnue_telekommynikacionnue_seti-152.png)
Рис. 5.4. Зависимость индивидуальных потерь Р одноканальных пользователей от изменения доли нагрузки шестиканальных пользователей и относительного порога 0]
Зависимость изменения индивидуальных потерь Р\ от изменения 0 и изменения
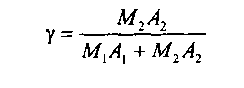
представлена на рис. 5.4.
Зависимость изменения индивидуальных потерь Р2от изменения 0] и у представлена на рис. 5.5.
Анализируя графики изменения Р\ и Р2от изменения относительного порога 0) и коэффициента у можно отметить, ЧТО ОНИ носят сложный волнообразный нелинейный характер. Эго не позволяет их прогнозировать, используя опыт и интуицию даже опытных специалистов в области телефонии.
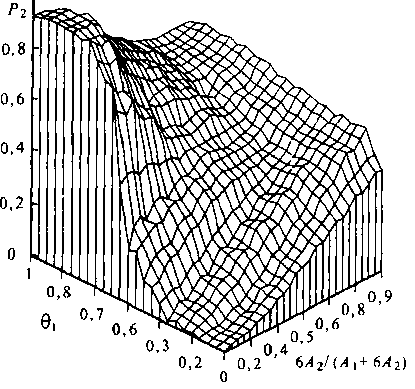
Рис. 5.5. Зависимость изменения индивидуальных потерь Р2шести канальных пользователей от изменения доли нагрузки шестиканальных пользователей и относительного порога 0
5.2.3. Результаты тестирования математической модели оценки качества обслуживания в системах коммутации с резервированием канальных ресурсов в направлениях связи Возможности математической модели, рассмотренной в предыдущем разделе, были исследованы на большом числе примеров коммутационных систем различной структуры. При этом результаты численных исследований этих КС сравнивались с результатами их имитационного моделирования. Ниже приведены примеры, иллюстрирующие возможности изложенного выше метода и эффективность применения резервирования канальных ресурсов при применении его для управления качеством обслуживания пользователей.
Для примера выберем пространственно-временную трехкаскадную КС типа «время - пространство - время», имеющую структуру
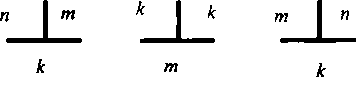
Для этой системы рассмотрим два случая резервирования канальных ресурсов. Первый случай соответствует двум однородным одноканальным пользователям (гомогенный трафик). Второй - случаю, когда один класс пользователей при установлении занимает один канал, а второй класс пользователей занимает одновременно шесть каналов (гетерогенный трафик).
Случай 1 - гомогенный трафик Коммутационная система с гомогенной нагрузкой и двумя классами пользователей. На рис. 5.6 представлены результаты теоретических расчетов вероятностей потерь вызовов и результаты имитационного моделирования для двух классов пользователей, занимающих при установлении соединения по одному каналу в КС. Им соответствуют потери вызовов соответственно Р\ и Рг. На рис. 5.6 представлены и средневзвешенные потери Р. Относительный порог первого класса пользователей меняется 9 = Var. Относительный порог второго класса пользователей 02 = 30. Квадраты (здесь и далее) - данные имитационного моделирования. Доверительные интервалы соизмеримы со стороной квадрата. При имитационном моделировании и расчетах было принято: п = т = 30, к = 30, т. е. емкость КС составляет N = 900 каналов. Предполагалось, что режим искания - «от точки к точке», число направлений связи h = 10, емкость пучка каналов в каждом направлении V = 30. Интенсивности поступающих нагрузок равны А, = 5 и А2= = 20 Эрл.
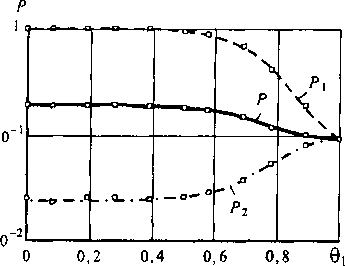
Рис. 5.6. Результаты теоретических расчетов вероятностей потерь при использовании резервирования канальных ресурсов для коммутационной системы:
□ - данные имитационного моделирования
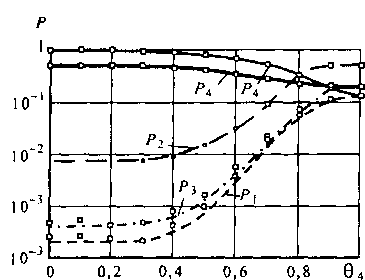
Рис. 5.7. Результаты численных исследований и результаты имитационного моделирования КС
Из рис. 5.6 можно сделать следующие замечания: данные имитационного моделирования и теоретические данные очень хорошо согласуются между собой; уменьшение относительного порога 01 увеличивает потери Р, и уменьшает потери Л; при 01 = 0 пользователи класса 1 не имеют доступа и Р\ = 1, потери вызовов пользователей класса 2 достигают своего теоретического минимума.
Изменение относительного порога 01 позволяет гибко и в широких пределах изменять вероятности потерь для обоих классов.
Коммутационная система с гомогенной нагрузкой и четырьмя классами пользователей. Эта КС характеризуется четырьмя однородными классами пользователей, требующими для своего обслуживания по 1-му каналу. Данные о ее структуре и нагрузках приведены на рис. 5.7. Графики построены для случая, когда интенсивности поступающих нагрузок и ограничительные пороги соответственно равны: А{= 1; А2= 3; Aj = 10; А4= 15; Т, = 30; Т2= 24; 7) = 28; Г4= var. Выводы, сделанные относительно исследования математической модели, исследованной на примере КС с двумя классами пользователей, оказываются полностью справедливыми и для КС с четырьмя классами пользователей.
Случай 2 - гетерогенный трафик Коммутационная система с гетерогенной нагрузкой и двумя классами пользователей. Структурные параметры этой КС следующие: п = m = 30, к = 10, V =■ 30. Поступающие нагрузки: А, = 12 и А6= 3 Эрл. Режим искания - «от точки к точке». Р - вероятность потерь одноканальных заявок, Р2- вероятность потерь шестиканальных заявок, Р - вероятность средневзвешенных потерь.
На графиках рис. 5.8 видно пересечение кривых Р\ и Р2, что говорит о возможности в случае гетерогенной нагрузки выравнивания потерь вызовов пользователей.
Коммутационная система с гетерогенной нагрузкой и двумя классами пользователей и расширением. Данная КС отличается от пре-
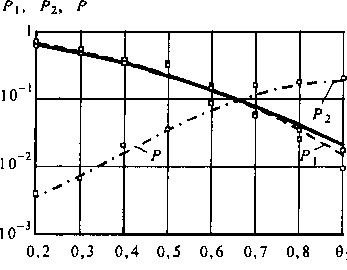
Рис. 5.8. Зависимость изменения вероятностей потерь РиР2и средневзвешенной вероятности потерь Р от изменения относительного порога 9,: кривые - теоретические результаты; □ - результаты имитационного моделирования
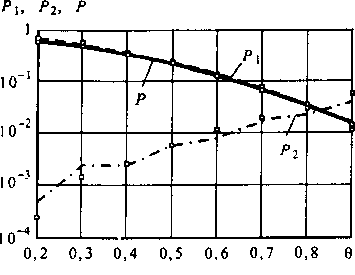
Рис. 5.9. Зависимость изменения вероятностей потерь РиР2, Р от изменения относительного порога 0, в КС с расширением дыдущей КС тем, что она имеет расширение, т. е. в этой системе число промежуточных путей больше числа входящего числа каналов.
Структурные параметры КС: п = 30, т - 36, к = 10, V- 30. Поступающие нагрузки: А\ = 12 и А6= 3 Эрл. Режим искания - «от точки к точке». Р\ - вероятность потерь одноканальных заявок, Р2- вероятность потерь шестиканальных заявок, Р - вероятность средневзвешенных потерь.
Анализируя графики, представленные на рис. 5.9, можно отметить, что увеличение числа промежуточных путей в КС приводит к смещению точки пересечения кривых (точку выравнивания потерь) в область более высоких значений относительного порога 0,.
⇐Результаты численных исследований системы с повторными вызовами | Мультисервисные телекоммуникационные сети | Управление канальными ресурсами цсис на основе канального резервирования⇒
