Перейдем к описанию метода, используемого для оптимизации целевой функции. В силу математической природы решаемой задачи будем использовать шаговый случайный поиск. Известны и исследованы различные алгоритмы такого поиска. Рассмотрим метод из класса так называемых локальных методов шагового поиска, которые достаточно подробно изучены и для них известны оценки скорости сходимости процесса поиска, среднего смещения к цели. Локальность выбранного метода обусловлена независимостью процесса поиска от его предыстории [8.11].

Анализ методов локального случайного шагового поиска показывает, что для решаемой задачи достаточно эффективно можно применить так называемый «алгоритм с возвратом при неудачном шаге» [8.10], особенностью которого является пониженная тенденция блуждания в области цели. Удачным шагом будем называть такой шаг, при котором численное значение целевой функции будет меньше ее значения на предыдущем шаге. Пусть в

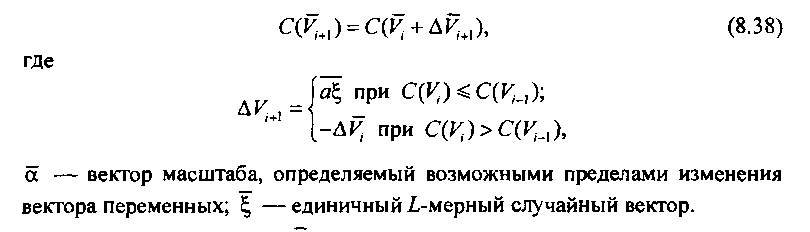
пространстве оптимизируемых параметров сделан некоторый случайный шаг из точки, характеризуемой вектором каналов и значением функции цели С(У,). В этом случае новая случайная точка будет характеризоваться вектором У_ми новым значением целевой функции С(У.₊₁). Если С(У_и1) < С(У_М), то предпринятый шаг считается удачным, если С(У₊₁) 2* С(У_М), то шаг считается неудачным и осуществляется возврат на предшествующий этап оптимизации. Формула этого алгоритма имеет следующий вид: С(У_м) = С(У,₊АУ₁₊₁), (8.38)

где при С(^)<С(К_М);

^М1-А^ при С(^)>С(^,), а - вектор масштаба, определяемый возможными пределами изменения вектора переменных; ^ - единичный /,-мерный случайный вектор.

Реализации вектора £ равномерно распределены во всем Х-мерном пространстве, причем -1 < £, < I, / = 1 ,Ь. Этот алгоритм оптимизации является целенаправленным благодаря возможности возврата при неудачном шаге. Для того чтобы сделать обратный шаг, данный алгоритм предполагает наличие памяти.

Рассмотрим особенности применения оптимизации целевой функции (минимизации функции капитальных затрат) с помощью алгоритма случайного поиска фрагмента сети и содержащего семь станций и два узла (рис. 8.7). Зададим следующий алгоритм маршрутизации: при необходимости уста-

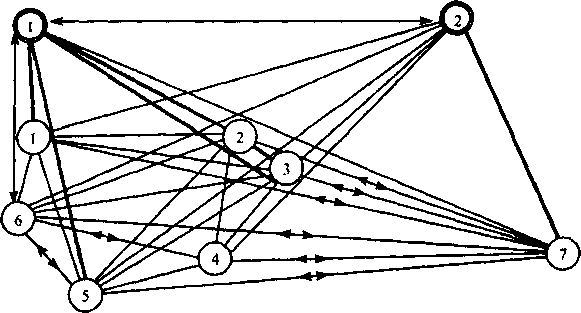
Рис. 8.7. Схема 2-узловой сети связи:

@- узел; О - станция;--ПП, ОПП;--ППВ

новления соединения между двумя станциями использовать принцип кратчайшего пути. Это означает, что на первом этапе соединения предпринимается попытка его установления по прямому пучку каналов между рассматриваемыми станциями. Если эта попытка оказалась неудачной, то предпринимается попытка установить соединение по обходному пути. При этом возможны два случая:

1) рассматриваемые станции включены в один и тот же узел. Тогда между станциями имеется только один обходной путь - ППВ с вероятностью потерь на каждом участке этого пути Р- 1 %;

2) рассматриваемые станции включены в различные узлы. Тогда между станциями имеются два обходных пути: ОПП и ППВ.

На рис. 8.7 показана сеть с максимально возможным в рамках введенных ограничений числом пучков каналов. Однако сеть, полученная в результате оптимизации, может иметь меньшее число пучков каналов между ее узлами. Структура такой сети при заданном качестве обслуживания на ППВ будет зависеть от вида матрицы нагрузок Д_уи матрицы стоимостей С_у, где Ау нагрузка, а Су - стоимость канала между станциями (узлами) г и j.

При оптимизации целевой функции необходимо определить число независимых переменных. В соответствии с требованиями, предъявляемыми к проектированию междугородной сети связи, для г-й станции суммарное число входящих и исходящих каналов, образующих используемые для связи с у-й станцией пучки ПП, должно выбираться кратным модулю уплотнения (30 каналов); с кратностью единица выбираются пучки ППВ.

Очевидно, что все пучки ПП так же, как и пучки ОПП, выбираемые с кратностью 12, в нашем случае являются независимыми переменными. Это означает, что размерность пространства, в котором будет проводиться оптимизация, Ь = 49. Эта величина обусловлена: числом всех ПП между станциями, которое равно 42; числом пучков ОПП, равным 6, между 1-Й станцией (г = 1, 6) и вторым узлом и пучком ОПП между седьмой станцией и первым узлом. Задавая случайным образом значения этих переменных, т. е. емкости пучков каналов между отдельными станциями, находим параметры всех избыточных нагрузок и, следовательно, емкость этих пучков каналов при фиксированной вероятности потерь на ППВ. Определив емкости пучков каналов на сети, можно найти значение целевой функции С.

Рассмотрим более подробно этапы работы алгоритма минимизации капитальных затрат на создание сети с помощью метода случайного поиска. Для того чтобы применить алгоритм метода случайного поиска с возвратом в исходную точку при неудачном шаге, требуется выбрать начальное значение целевой функции. Это можно сделать различными путями. Исследования, проведенные в [8.10], показывают, что для ускорения сходимости целесообразно организовать для отыскания начального значения целевой функ

ции этап пассивного случайного поиска, который позволит определить «наилучшую начальную пробу». Дальнейший поиск по данному алгоритму будет осуществляться от наилучшего значения целевой функции, найденного на этапе пассивного поиска. Необходимое число шагов для реализации пассивного случайного поиска может быть оценено с помощью формулы [8.12]: Л-= (8.39)

1*1-?)

где W - вероятность нахождения значения целевой функции в выбранной области ее наилучших значений; q - величина области наилучших значений функции цели.

Пусть, например, область наилучших значений целевой функции <7 = 0,010; тогда при вероятности нахождения одного из значений целевой функции W - 0,95 получаем, что для поиска минимума целевой функции необходимо N- 30 шагов.

Сделаем несколько замечаний относительно выбора величины рабочего шага. Так как для рассматриваемой задачи максимальное изменение суммарной емкости пучков каналов путей первого и второго выбора соответствует одному модулю, это и определяет величину смещения вектора по каждой координате в /,-мерном пространстве:

-1, если 0<а<1/3;

= < 0, если 1/3 < 2/3;

+ 1, если 2/3 < а <1, где а - случайное число, равномерно распределенное между 0 и 1.

После выполнения рабочего шага определяется число модулей на пучках первого и второго выбора, а затем суммарное число исходящих и входящих каналов в соответствующих направлениях на ППВ. Это суммарное число каналов распределяется по исходящей и входящей связям так, чтобы обеспечить минимум суммарной избыточной нагрузки. Ее параметры на соответствующих пучках каналов определяют по формулам (8.31)-(8.37), затем рассчитывают емкость пучков каналов последнего выбора. После того, как определены все пучки между станциями и узлами, вычисляют значение целевой функции C^w, если это был z'-й шаг поиска. Дальнейший процесс поиска описывает формула

(8.38). Укрупненная блок-схема алгоритма оптимизации сети по критерию стоимости МСП приведена на рис. 8.8.

Сеть, показанная на рис. 8.7, была оптимизирована с помощью приведенного алгоритма МСП. Исходными данными для оптимизации являлись: матрица нагрузок Щ..Ц между станциями (табл. 8.2), матрица стоимостей

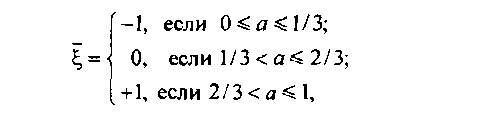
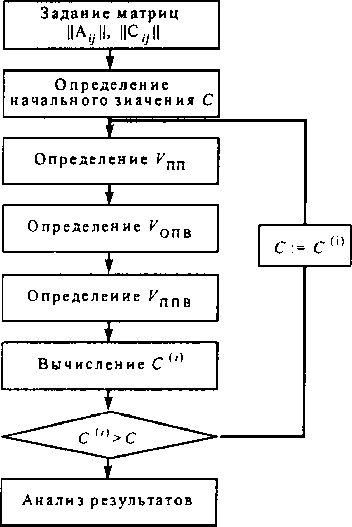
Рис. 8.8. Укрупненная блок-схема алгоритма оптимизации сети по критерию стоимости МСП

одного канала между узлами и станциями сети ЦС^.Ц (табл. 8.3). Предполагалось, что все станции и узлы не имеют внутренних блокировок, т. е.

= 1. В качестве начального приближения была использована оптимизированная по методу [8.4] матрица пучков каналов, приведенная в табл. 8.4. Стоимость оптимизации этого варианта сети составляет 730,12 у. е.

Результат оптимизации сети с помощью МСП иллюстрирует матрица каналов (табл. 8.5), соответствующая 182-м шагам поиска. Капитальные затраты этого варианта распределения каналов составляют С = 725,96 уел. ед., что на 0,6 % дешевле варианта, полученного по критерию [8.4].

При увеличении числа шагов поиска до 500 не было найдено варианта организации связи с меньшими капитальными затратами. Как видно из сопоставления результатов оптимизации по методу [8.4] и МСП, варианты распределения каналов незначительно отличаются друг от друга и близки по стоимости. Это позволяет сделать вывод, что допущения, принятые при выводе критерия [8.4], являются вполне приемлемыми и не приводят к существенной погрешности при расчете пучков каналов на сети.

Таблица 8.2*

i ___ j __

_ C I С₂I Сч С₄1 С₅I с₆С₇

С, 0 1,5 0 0,6 97,3 2,8 0,8

С₂1,4 0 2,7 1,3 120,3 19,4 1,1

С₃15,8 4,7 0 2,8 160,9 7,4 7,4

С₄0,4 1,0 1,5 0 167,0 2,2 1,5

С₅10,2 16,1 24,1 30,9 0 183,0 21,3

С₆3,3 7,4 5,1 3,3 25,5 0 1,5

Ci 0,7 0,6 7,4 1,2 141.3 1.2 I 0

Таблица 8.4

Таблица 8.5

Для указанных выше условий была проведена также оптимизация сети по МСП в предположении, что на всех станциях и узлах допускаются внут ренние блокировки, величина которых определяется выбором Fd = 0,8. Результат оптимизации емкостей пучков каналов сети с помощью МСП приведен в табл. 8.6. Анализ таблицы показывает, что переход от полнодоступных пучков (Frf = 1) каналов на сети к пучкам с блокировками (Fd = 0,8) увеличивает затраты примерно на 7 % (С = 775,95 уел. ед.). Последнее обстоятельство говорит о необходимости обобщения критерия [8.4] для случая полнодоступных блокируемых пучков каналов.

Таблица 8.6

Исследования показали, что принятые в [8.4] при построении оптимизационной модели допущения (второе и третье) приводят к незначительной погрешности при распределении пучков каналов на сети связи. Однако предположение о неблокируемости пучков каналов (первое допущение) приводит к заметному снижению числа каналов на сети. Результатом этого является повышенная чувствительность сети к перегрузкам и, как следствие, снижение качества обслуживания абонентов. Учесть структуру узлов коммутации при распределении каналов на сети можно по-разному. Один из возможных подходов рассмотрен в [8.2].

Более детально с оптимизацией структуры ЦСИС по критерию минимума стоимости можно познакомиться в [8.9].

⇐Оценка точности метода оптимизации сети по критерию минимума капитальных затрат | Мультисервисные телекоммуникационные сети | Литература⇒