Решение оптимизационных уравнений (8.2), (8.6), (8.9) для соответствующих базовых сетевых структур позволяет определить оптимальные структурные параметры данных фрагментов сети при заданном ограничении на качество обслуживания. Однако итерационная процедура получения такого решения даже для простейшей 3-узловой структуры является достаточно трудоемкой, что приводит к необходимости использования аппроксимаций, которые позволяют снизить объем вычислений и, в то же время, гарантируют достаточно надежные оценки рассматриваемых параметров сети.

Проведенные исследования [8.12] показали, что при решении оптимизационных уравнений для базовых структур У-ЦСИС (см. рис. 8.3 и 8.4) целесообразно для оптимизации сети коммутации каналов иерархической структуры использовать аппроксимации, предложенные в работах [8.8, 8.13, 8.14], так как они позволяют учесть модульность систем передачи, структуру коммутационного поля УК и алгоритм установления соединения и при этом значительно сократить объем вычислений.

Рассмотрим сначала алгоритм вычисления емкостей пучков каналов в 3-узловой базовой структуре (см. рис. 8.3). В соответствии с оптимизационным уравнением (8.3) для данной базовой структуры процедура его решения носит итерационный характер и включает следующие операции.

1. Задать начальные значения [3? и (Зз.

2. Вычислить значение Н\ в соответствии с уравнением (8.3):

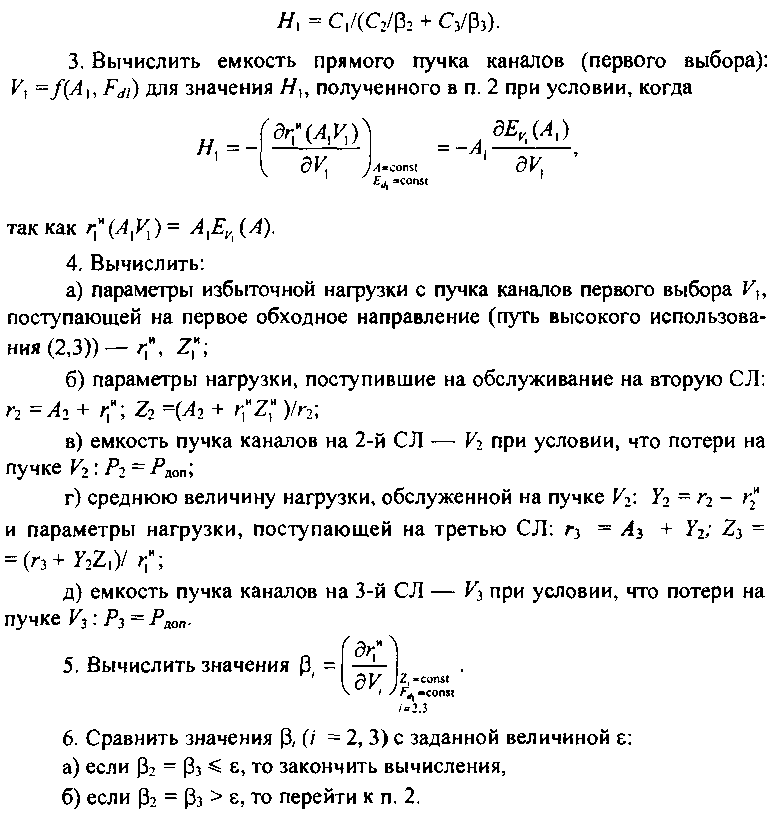
Практика использования данного подхода при оптимизации реальных иерархических сетей КК показала, что хорошая сходимость алгоритмов вычисления базовых структур достигается при задании начальных значений р, (/ = 2, 3), равных 0,7-0,8.

Как показали исследования [8.6, 8.8, 8.12], Z-аппроксимация является наиболее эффективным методом для расчета вероятности потерь в УК с внутренними блокировками на сетях с обходными путями и определения емкостей пучков каналов. Эта аппроксимация и основные расчетные соотношения для нахождения параметров нагрузки и коэффициента дисперсии Z рассмотрены в гл. 6.

В соответствии с этой аппроксимацией вероятности потерь вызовов на пучке каналов емкостью V и эффективной доступностью d₃, на который поступает нагрузка с параметрами (R„ Z,), Z, > 0, определяется как

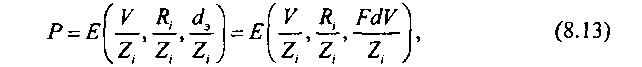
где Е(% •, •) - формула Эрланга для идеального неполнодоступного включения.

По формуле (8.13) вычисляют избыточную г" и обслуженную У нагрузки при условии, что на пучок каналов поступает непуассоновская нагрузка с параметрами (Л„ 2“).

Кроме того, можно получить оценки коэффициентов дисперсии избыточной 2* и 2_Уобслуженной нагрузок при условии, что на пучок каналов поступает нагрузка с параметрами (Л„ Д).

При решении задач оптимизации сети в процессе ее проектирования коэффициент доступности Ра считается известным и также задаются допустимая величина потерь вызовов на пути последнего выбора и параметры исходной нагрузки (К, 2). При этом (8.13) является нелинейным уравнением с одним неизвестным - емкостью пучка каналов V. При этом емкость V определяется с учетом структуры УК.

Таким образом с помощью формулы (8.13) можно определить емкости пучков каналов в пучках высокого использования и пучков каналов в путях последнего выбора. Из приведенного алгоритма расчета 3-узловой базовой структуры следует, что емкости пучков каналов первого выбора (на прямых путях) находятся из решения уравнения

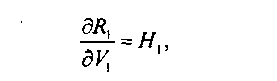
при фиксированной поступающей на этот пучок нагрузке А \ и коэффициенте доступности где параметр Н\ является константой и определяется в процессе оптимизации.

Процесс вычисления является итерационной процедурой. Дальнейшие исследования показали, что поскольку на данном этапе оптимизации оцениваются только границы изменения переменных, то допустима некоторая погрешность в определении емкостей пучков и можно использовать приближенные формулы, которые позволяют избежать большого числа итераций.

Так, для определения максимальной емкости пучка У„_мхпервого выбора при ^ » 1, когда систему можно считать неблокирующей, а Р = 1 %, предлагается аппроксимация вида степенной функции, коэффициенты которой зависят от маргинального использования этого пучка каналов (для базовой структуры, представленной на рис. 8.5):

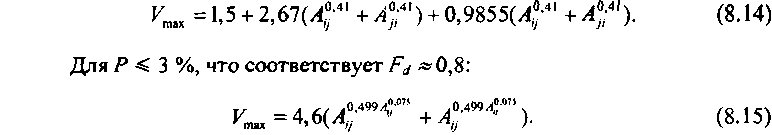
Формулы (8.14) и (8.15) получены в результате применения линейной регрессии при аппроксимации формулы (8.13).

Если пучки каналов имеют модульную структуру с емкостью модуля, равной М, то число модулей в этом случае

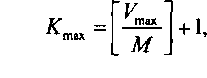
где [•] - целая часть числа.

Аналогичные формулы можно использовать при определении емкости пучков каналов на обходных путях следующего выбора, не являющихся одновременно путями последнего выбора.

Например, для базовой структуры, представленной на рис. 8.3, эти формулы имеют следующий вид:

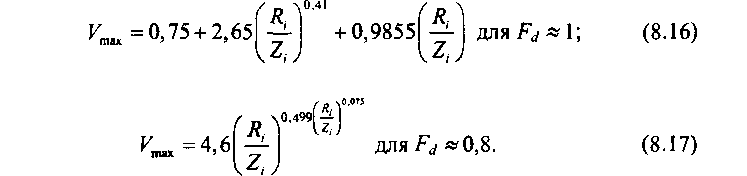
Емкости пучков каналов последнего выбора вычисляют при фиксированных значениях величины потерь Р_аоп-Ри ДЛЯ пути последнего выбора и коэффициента доступности при определении производной вида:

При обосновании общности критерия оптимизации трехузловой базовой структуры (8.6) был осуществлен переход к конечным разностям при определении производных. Однако при проведении вычислений замена производных конечными разностями может привести к погрешности, величина которой зависит от соотношений структурных и нагрузочных параметров. В работе [8.8] показано, что в случаях, когда требуется знание производных типа д/{Р)!дУ, где /(Р) - некоторая функция, зависящая от вероятности потерь, задача может быть сведена к использованию конечных разностей лишь при условии, что величина А Vдостаточно мала АУ & 0,01. Однако требование выбора АУ « 1 приводит к необходимости использования интегральных представлений для таких формул как первая формула Эрланга и формула для идеального неполнодоступного включения Эрланга.

Вопрос об эффективности в вычислительном отношении интегральных представлений этих формул подробно рассмотрен в гл. 6, где даны рекуррентные формулы для проведения вычислений при условиях, что пучок каналов V и доступность (1 являются нецелочисленными. При вычислении емкостей полнодоступных пучков каналов можно использовать аппроксимацию первой формулы Эрланга, предложенную в работе [8.14]:

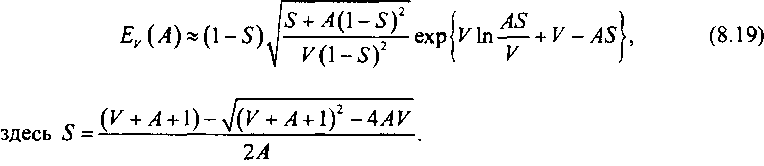
Учитывая, что искомая производная (8.18) вычисляется при фиксированном значении Р„ = const, можно записать:

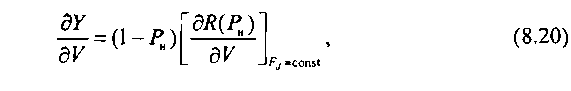
где Я(Р_Н) - поступающая непуассоновская нагрузка в точке Р».

Из выражения (8.20) следует, что производная дЯ/дУ определяется в точке Р„, поэтому можно принять:

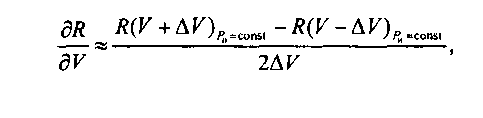
где R(F+ AV) и R(V- AV) - значения нагрузки R в точках (V + AV) и (V- AV), соответственно, при Р„ = const. Так как для реальных систем Fj < 1, то для определения величин R(V + AV) и R(V - AV) используют соотношение

(8.13), которое связывает между собой потери, нагрузку, емкость пучка и величину доступности.

Учитывая (8.13) и, что Р_н= const, можно записать:

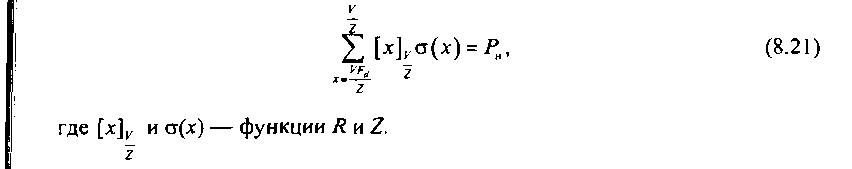
На основании полученных ранее соотношений, (8.21) можно представить как уравнение вида R=f(V), при F_d- const, Z= const. Решить уравнение (8.21) можно с использованием итерационной процедуры, предполагающей нахождение производной вида:

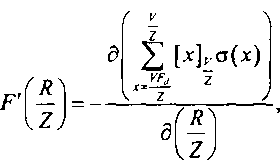
что является довольно трудоемкой задачей.

Для сокращения объема вычислений была использована аппроксимация, дающая хорошие результаты для значений /V, находящихся в пределах 0,8 <^<1:

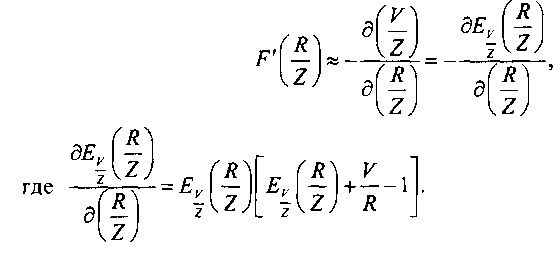
Исследование характера этого итерационного процесса решения уравнения (8.21) показало, что данная аппроксимация для Р(Я/2) при Р„ = 1 % обеспечивает хорошую сходимость при относительной погрешности в определении Я, равной е = 0,0005.

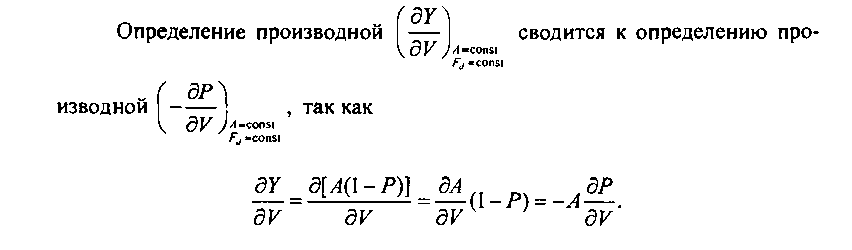
Таким образом, для искомой производной может быть найдено только численное значение с использованием интегрального представления этой формулы.

После определения емкостей пучков каналов СЛ, составляющих путь последнего выбора, можно вычислить маргинальные нагрузки (Зг и (З3:

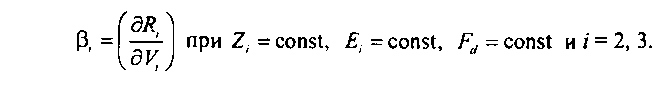
В данном случае производная вычисляется аналогично описанному выше для вычисления производной (8.18).

При решении оптимизационного уравнения (8.6) для базовой структуры, представленной на рис. 8.5, задача сводится к рассмотрению двух 3-узловых базовых структур, на которые декомпозируется рассматриваемая структура. Каждая из базовых структур оптимизируется независимо в соответствии с рассмотренным выше алгоритмом. Емкости пучков каналов в прямом и обратном направлениях СЛ определяются, исходя из условия модульности их изменения, т. е. число модулей в пучке равно:

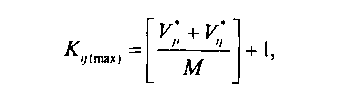
где ^7, - емкость пучка, полученная при раздельной оптимизации; М - емкость модуля первичной группы каналов.

Затем проводят деление емкости пучка каналов между двумя потоками нагрузки, проходящими по ней: прямым и обратным.

Проведенный анализ различных стратегий разделения общего прямого пучка (пути 1-го выбора) показал, что оптимальной является стратегия, соответствующая делению пропорционально решениям, полученным в результате раздельной оптимизации двух 3-узловых структур, как более эффективная в смысле достижения глобального минимума и минимального числа вычислений. В этом случае величины У_1}и Уц определяются пропор

⇐Оптимизационные уравнения базовых сетевых структур | Мультисервисные телекоммуникационные сети | Оптимизация пучков каналов при неординарных пуассоновских потоках на пучках пути первого выбора⇒