При решении задач оптимизации функционирования информационных сетей, разработке методов маршрутизации на ЦСИС возникает задача определения параметров нагрузки отдельных направлений искания узла автоматической коммутации (УАК). Такая нагрузка, как показано выше, носит непуассоновский характер, ее параметры зависят не только от емкости пучка каналов, но и от структуры КС узла, загрузки, алгоритма работы УАК. В большинстве исследований, связанных с оптимизацией функционирования сети связи в силу значительной сложности задачи обычно пренебрегают влиянием структуры КС УАК на характер нагрузки в направлениях связи, что приводит в ряде случаев к существенному загрублению математических моделей. Особенно сильно проявляется влияние структурных и нагрузочных характеристик УАК на параметры нагрузки в направлениях связи, характеризующихся большой вероятностью возникновения избыточной нагрузки. Многочисленные исследования показали, что при решении ряда задач для описания свойств нагрузки достаточно использовать первые два момента распределения: математическое ожидание интенсивности нагрузки Я, и дисперсию а-. В некоторых случаях удобно задавать нормированную дисперсию 2, = сг / /?,, называемую часто коэффициентом дисперсии. Задача определения дисперсии обслуженной и избыточной нагрузок, возникающих в направлениях искания УАК, до настоящего времени строгого решения не получила даже для случая, когда поступающая на направление нагрузка является пуассоновской. Большие трудности возникают при описании обслуженной и избыточной нагрузки, если поступающая нагрузка является непу-ассоновской. Тем не менее в некоторых случаях появляется возможность 6 - 7791

получения простых и в то же время достаточно надежных аппроксимаций для дисперсии нагрузки. В этом отношении весьма интересным представляется подход, предложенный в работе [6.3] и развитый для полнодоступного пучка каналов. Основываясь на подходе [6.3], рассмотрим вопрос о величине дисперсии нагрузки, учитывая при этом структуру КС, ее загрузку и режим искания.

Пусть на некоторое направление искания УАК, имеющее V каналов и характеризующееся эффективной доступностью с/, поступает нагрузка, задаваемая парой (7?„ 2) с 2₁> 0. Как было показано, вероятность потерь в этом направлении может быть аппроксимирована выражением

где Е(■ ■ •) - третья формула Эрланга. Эффективная доступность, входящая в (6.20), определяется через семиинварианты мгновенной доступности и учитывает структуру и загрузку КС, а также алгоритмы выбора свободного пути. Метод определения эффективной доступности подробно рассмотрен в гл. 3. В дальнейшем будем считать ее известной. Формула (6.20) позволяет определить величину избыточной Я₀и обслуженной нагрузки У при условии, что на направление искания поступает непуассоновская нагрузка (Л_;, 2_п):

Согласно [6.2], вероятность потерь (6.20) трактуется как вероятность потерь в одной из Ъ, коммутационных подсистем с емкостью пучка V = У/г,, эффективной доступностью ^ /1₁и нагрузкой /?, =/?,/2, . Такая декомпозиция исходной КС соответствует случаю максимальной корреляции нагрузок (как обслуженной, так и избыточной) отдельных подсистем. Учет этого обстоятельства позволяет получить оценки коэффициента дисперсии избыточной и обслуженной нагрузки 2$ при условии, что на направление искания поступает непауссоновская нагрузка (/?,, Ц).

Проводя рассуждения, близкие к [6.2], и учитывая результаты, полученные в работе [6.3], находим формулу коэффициента дисперсии избыточной нагрузки:

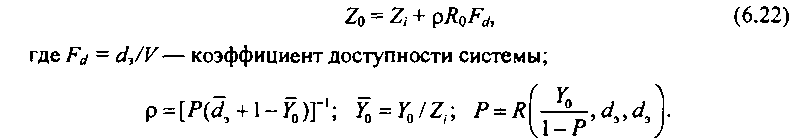
Если на направление искания УК поступает пуассоновская нагрузка, т. е. 2,- = 1, то формула (6.22) переходит в соответствующую формулу Герцога [6.4].

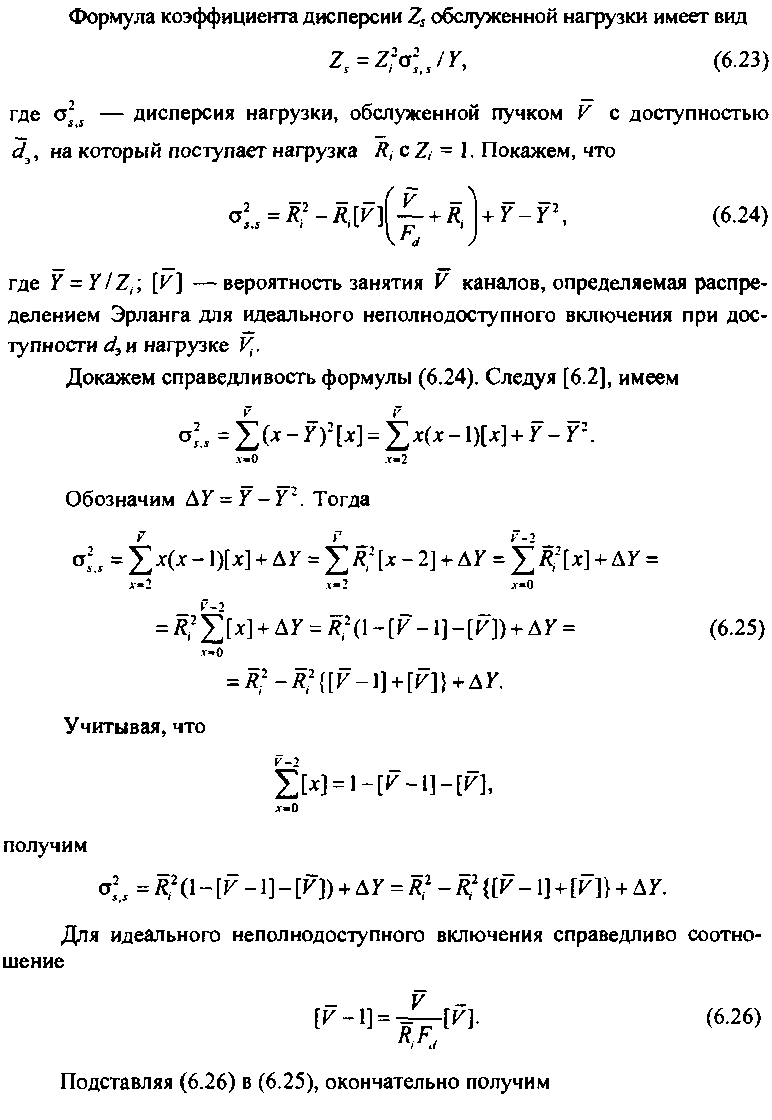
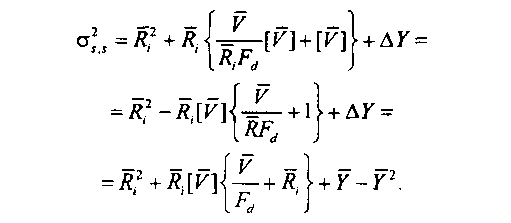
<₁= л₍ ²₊/г,{-р_Г ^[к^] + ^[к^]}₊дг =

= Щ-яХуц-1-+\\+ьу =

да I

= Д²+Л,[К]-^+Л,₊У-Г².

Заметим, что при 2 = 1 и Р_<1= 1 формула (6.24) переходит в известную формулу дисперсии нагрузки, обслуженной полнодоступным пучком каналов (формула Риордана-Вилкинсона).

Проиллюстрируем приведенные формулы (6.20)-(6.24) численным примером. Пусть на направление узла автоматической коммутации поступает нагрузка с параметрами Яс/ = 6 Эрл и = 2. Считаем, что емкость пучка каналов в рассматриваемом направлении У= 10 каналов. Предположим, что структура узла коммутации и его загрузка таковы, что с1₃= 8. Требуется определить вероятность возникновения избыточной нагрузки Р, математическое ожидание интенсивности избыточной Я₀и обслуженной Я_хнагрузок, а также коэффициенты дисперсии 2$ и 2₅.

Используя для расчета интересующих характеристик формулы (6.20)-(6.24), получим Р = 0,1275, Д₀= 0,7652, У = 5,2348,2_й= 3,44,2₃= 1,73.

Анализируя результаты расчета, необходимо отметить, что:

2о > 2„ т. е. избыточная нагрузка имеет относительно больший разброс, чем поступающая нагрузка;

2_$< Д, т. е. обслуженная нагрузка имеет относительно меньший разброс, чем поступающая нагрузка, но при этом она остается значительно «хуже» пуассоновской нагрузки, так как 2₅> \.

Формулу (6.22) можно применять при решении сетевых задач с многократными обходами, а формулу (6.23) - при решении сетевых задач, в которых каналы направления искания являются источниками новых вызовов, создающими нагрузку на последующие узлы коммутации.

Литература 6.1. Ершова Э.Б., Ершов В.А. Цифровые системы распределения информации. М.: Радио и связь, 1983.

6.2. Теория телетрафика. Штермер X., Белендорф Э., БининдаН. и др. / Под ред. Г.П. Башарина. М.: Связь, 1971.

6.3. Fredericks A.A. Congestion in blocking systems - a simple approximation technique //Bell Syst. Techn. J. 1980. Vol. 59. N. 6. P. 805-827.

6.4. Herzog U., LotzeA. Das RDA-Verfahren, ein Streuwertverfahren fur unvollkommene Bundei // NTZ Rep. 1966. N. 19. P. 640-646.

6.5. Katayama T„ Sumita S., Inamori H. Study on Traffic Design Method for Resource Sharing in Integrated Services Networks// Review of the Electrical Com. Lab. 1986. Vol. 34. N. 5.

6.6. LindbergerK. The Qualities of Overflow Traffic. An Extension of a Simple Approximation Method: Report in Swedish TELEVERKET, 1981.

Оптимист считает, что мы живем в лучшем из миров, пессимист опасается, что это так и есть.

Из разговора 7. УПРАВЛЯЮЩАЯ СИСТЕМА УЗЛА ЦСИС КАК СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ С ОГРАНИЧЕННЫМ ВРЕМЕНЕМ ОЖИДАНИЯ И КОНЕЧНОЙ ОЧЕРЕДЬЮ

⇐Средневзвешенная вероятность потерь | Мультисервисные телекоммуникационные сети | Полнодоступный пучок обслуживающих приборов с ограниченным ожиданием и конечной очередью⇒