Основные характеристики. Системы, в которых существует единственный промежуточный путь между парой вход-выход, могут иметь любую емкость, а соединения осуществляются через смежные каскады. Такие КС называются системами типа Баньян (КС-Б) [10.11]. Различают несколько типов сетей Баньян (см. рис. 10.9).

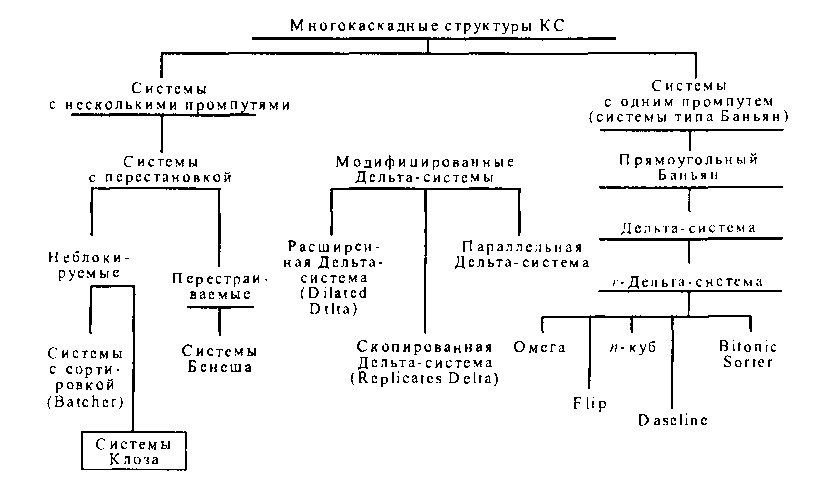
Рис. 10.9. Классификация КС для узлов Ш-ЦСИС

КС-Б, в которых число входов N равно числу выходов М, получили название прямоугольных систем. Эти системы характеризуются следующими свойствами:

• все соединения устанавливаются через смежные каскады;

• все КЭ имеют одну и ту же емкость: п входов и п выходов;

• число коммутаторов каждого каскада к = ЛУп;

• число каскадов 5 = log„ N.

Заметим, что часто прямоугольные КС типа Баньян, в которых установление соединения осуществляется на основе числового управления, называются Дельта-системами. Для них характерно побитовое управление, которое также называется самомаршрутизацией.

Так как число каскадов системы 5 = ^„N5 то каждый выход может быть закодирован 5 «-разрядными цифрами. Эти коды представляют собой адреса точки назначения, приписываемые ячейкам, проходящим через систему коммутации. Предполагается, что путь между любым входом и выходом может быть найден за 5 шагов. Пример такой процедуры показан на рис. 10.10. В этом случае адрес точки назначения состоит из 3 бит.

Предположим, что требуется передать ячейку, поступившую по входу с номером 0 второго коммутатора первого звена на выход с номером 0 второго коммутатора последнего звена. Данный выход будет иметь код 010. Поэтому дополнительный адрес, приписываемый ячейке, будет также 010.

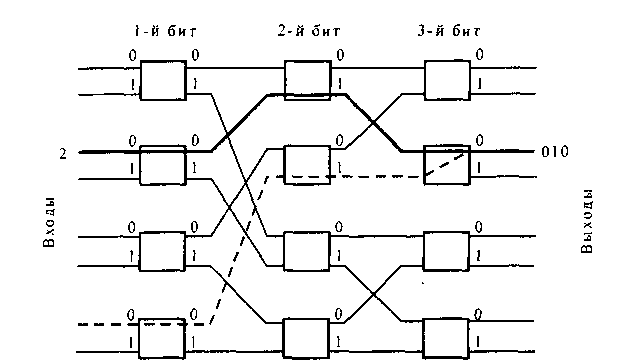
Рис. 10.10. Иллюстрация процедуры побитового управления в Дельта-системе емкостью 8x8

В соответствии с этим адресом в самомаршрутизирующейся Дельтасистеме во втором коммутаторе первого каскада будет осуществлено соединение типа транзит, т. е. нулевой вход этого коммутатора будет соединен с нулевым выходом. В первом коммутаторе второго каскада будет осуществлено соединение типа транзит первого входа с первым выходом. И, наконец, во втором коммутаторе третьего каскада будет также осуществлено соединение типа транзит, т. е. нулевой вход второго коммутатора будет соединен с нулевым выходом. Это соединение на схеме рис. 10.10 показано сплошной жирной линией.

Если теперь потребуется установить соединение между входом 0 коммутатора 4 первого каскада и выходом 0 второго коммутатора третьего каскада, то маршрут будет выбираться по-прежнему в соответствии с двоичным кодом выхода 010. Этот маршрут на рис. 10.10 изображен пунктирной линией. Особенностью этого маршрута является то, что во втором коммутаторе третьего каскада требуется установление соединения типа кросс, т. е. вход с номером 1 должен быть соединен с выходом 0. Если на входах 2 и 6 появятся одновременно ячейки, требующие маршрутизации на выход 2, то возникает конфликт, и должно быть принято решение о блокировке одной из ячеек.

Рассматриваемая схема не является симметричной и свойство само-маршрутизации оказывается справедливым, если соединение устанавливается от входов к выходам. Система не обладает свойством самомаршрутиза-ции, если соединение устанавливать от выходов ко входам.

Класс Дельта-систем, в которых свойство самомаршрутизации справедливо в обоих направлениях (от входов к выходам, и наоборот), называется реверсивными Дельта-системами или г-Дельта-системами.

Топология Дельта-систем. Существует много различных топологических структур Дельта-систем, например, Омега, Flip, N-Куб, Baseline [10.11]. Отличие этих топологических структур состоит в особенностях допустимых перестановок, реализующих межкаскадные отображения входов на выходы.

При построении Дельта-систем используют три базовых типа перестановок:

• совершенные перестановки (тасовка) Q;

• несовершенные перестановки Q“¹;

• P-перестановки (куб).

Эти перестановки определяются следующим образом. Пусть Cj = ~ ((s-b h-г, h, /о)^естьбитовое слово, представляющее г'-й вход-выход коммутационного каскада. Тогда:

- совершенная перестановка (Q):

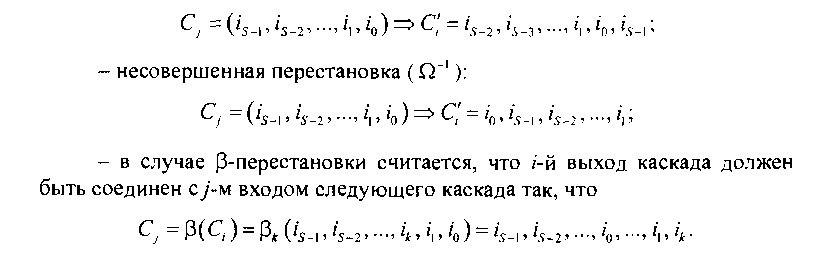
Используя вышеуказанные перестановки, можно определить следующие топологические структуры:

• Омега - Дельта-система, в которой каждому коммутационному каскаду предшествует совершенная перестановка межкаскадных звеньев;

• Flip - Дельта-система, в которой каждому коммутационному каскаду предшествует несовершенная перестановка межкаскадных звеньев;

• jV-куб (прямой jV-куб) - Дельта-система, в которой первому коммутационному каскаду предшествует несовершенная перестановка межкаскадных звеньев, тогда как 5-му каскаду (1 < 5 < 5- 1) предшествует р₅__Лперестановка;

• непрямой ./V-куб - Дельта-система, в которой за 5-м каскадом (1 < 5 < 5 - 2) следует Д+1 перестановка, а последнему каскаду (5 = 5-1) соответствует совершенная перестановка;

• Bitonic Sorter (коммутирующий Баньян) - Дельта-система, в которой за 5-м каскадом следует P*+i перестановка. Другими словами, Bitonic Sorter представляет собой N-куб систему, в которой отсутствует несовершенная перестановка;

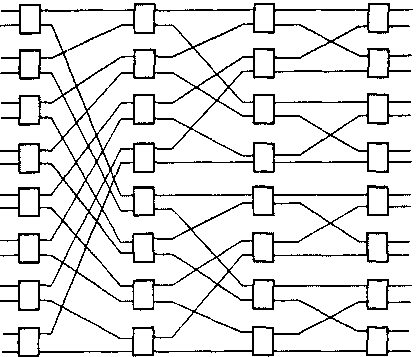
Рис. 10.11. ВаэеНпе-система

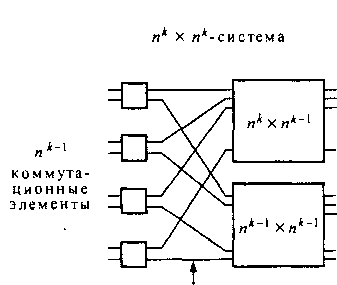
Рис. 10.12. Рекурсивная Baseline система

• реверсивная коммутирующая Баньян-система - Дельта-система, в которой 5-му каскаду (1 < 5 < 5- 1) предшествует перестановка. Иначе говоря, реверсивная коммутирующая Баньян-система есть А^-куб-система, в которой отсутствует несовершенная перестановка.

На рис. 10.11 показан частный случай Дельта-топологии - ВаБеПпе-системы.

На рис. 10.12 представлен &-й порождающий шаг рекурсивного процесса г1^к)хп^{к). ВаБеНпе-систему можно построить путем параллельного объединения п ВазеНпе-систем, емкость которых п^(кЛ)хп^(кЛ\ а также путем добавления дополнительного коммутационного каскада, составленного из пу.п коммутационных элементов. Звенья между дополнительным каскадом и п^(кл)*г1^кл)блоками должны быть упорядочены в соответствии с несовершенной перестановкой.

Хотя и существует много различных топологий КС, однако можно показать, что все Дельта-системы являются топологически функционально эквивалентными [10.11]. Другими словами, некоторая частная Дельтасистема может быть получена из другой Дельта-системы путем простого переупорядочения КЭ в промежуточных каскадах и в конечном счете путем соответствующей перенумерации либо входов, либо выходов. Так, например, на рис. 10.13 изображена топологическая эквивалентность системы Омега и А'-куб. В этом случае достаточно переупорядочить КЭ второго и третьего каскадов в соответствии с порядковым номером, приписанным каждому коммутатору.

Топологическая и функциональная эквивалентность Дельта-сисгем приводит к тому, что их характеристики - пропускная способность и за

Рис. 10.13. Топологическая схема системы ( Омега ]

держка - являются полностью независимыми от конкретной топологии. Исходя из этого, любые топологии можно использовать для построения системы БКП Ш-ЦСИС.

10.7. Коммутационные системы с несколькими промежуточными путями В КС с несколькими промежуточными путями (КС Hi 111) существует более чем один путь между парой вход-выход. КС с одним промежуточным путем между парой вход-выход характеризуются высокой вероятностью блокировки. В отличие от них система КП НПП позволяет минимизировать вероятность блокировки и в некоторых случаях делать систему неблокируемой [10.10]. Однако улучшенные характеристики БКП достигаются более высокой сложностью аппаратных средств. При этом в большинстве случаев теряется свойство самомаршрутизации, что делает необходимым введение централизованного устройства маршрутизации.

Различают два класса КС НПП:

• перестановочные системы (permutation networks);

• модифицированная Дельта-система.

Рассмотрим основные структурные особенности коммутационных систем с несколькими промежуточными путями между парой вход-выход.

Перестановочные системы. Класс перестановочных систем включает в себя системы, структура которых способна гарантировать ЛИ отображений входов на выходы. Другими словами, такие системы могут осуществлять соединения входов с выходами в любых комбинациях при условии, если не возникает ситуации, когда два входа одновременно потребуют соединения с одним и тем же выходом.

Перестановочные системы называют также перестраиваемыми, если существующие соединения можно переустановить так, что всегда будет установлено новое соединение между требуемым входом и выходом. Если новое соединение можно установить без перестроений, то такие системы называют неблокирумыми [10.10].

Классическим примером КС с перестроениями являются системы Бенеша [10.12, 10.13]. Пример системы Бенеша показан на рис. 10.14. Эта сис-

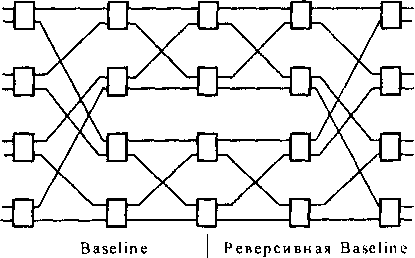
Рис. 10.14. Система Бенеша 8x8

тема образуется объединением двух систем, а именно: системы типа Baseline и системы типа реверсивная Baseline, в которой последний каскад первой системы и первый каскад второй системы соединяются между собой. Система, построенная таким образом, имеет 21og„iV-l каскадов и N/n путей между соединяемыми входами и выходами.

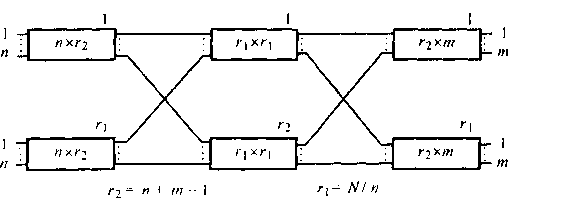
Коммутационная система Клоза [10.10] представляет наиболее интересный пример неблокируемой системы (рис. 10.15). Ее часто применяют в современных цифровых станциях. Типичная система Клоза состоит из трех каскадов; первый и последний каскады имеют соответственно КЭ емкостью п х г₂и г₂х т (п - число входов в каждый КЭ первого каскада, т - число выходов из каждого коммутатора третьего каскада, г₂- число коммутаторов второго каскада). Емкость КЭ второго каскада равна г_хх г_х(г\ - число коммутаторов первого (третьего) каскада). Таким образом, система Клоза имеет г₂промежуточных путей между каждым коммутатором первого и третьего каскадов. Система Клоза называется системой неблокируемой в строгом смысле, если выполняется условие

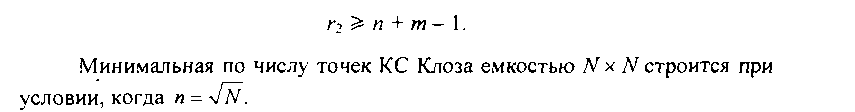
Как в системе Ьенеша, так и в системе Клоза маршрутизация ячеики осуществляется с помощью централизованного управляющего устройства, которое имеет информацию о состоянии системы и может найти свободный путь от входа к требуемому выходу.

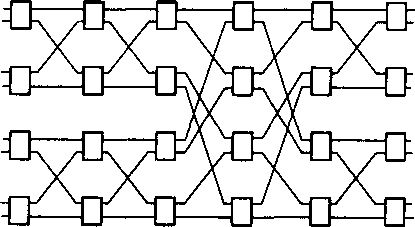
Система с сортировкой (Batcher system) представляет собой пример неблокируемой системы с распределенным управлением [10.16]. Эта система, называемая также сортирующей системой (Sorting system), дает возможность передавать к выходам любые Рис. 10.16. Схема системы Бэтчера 8 х 8 произвольные последовательности ячеек, поступающие по ее входам в соответствии с адресами назначения.

Каждый КЭ сравнивает адреса входящих ячеек и распределяет ячейку с наивысшим разрядом адреса к нулевому выходу, а ячейку с низшим разрядом адреса - к первому выходу. Так как распределение ячеек осуществляется по принципу каскад за каскадом путем сравнения адресов, то системе с сортировкой не нужно централизованное устройство управления. Однако распределенное управление требует большого числа каскадов. Фактически, система емкостью N* N требует log_nN(log„ N +1)/ 2 каскадов. Пример системы Бэтчера 8x8 показан на рис. 10.16.

Модифицированная Дельта-система. Модифицированные Дельтасистемы основаны на так называемых простых Дельта-топологиях. Эти системы приспособлены определенным образом для создания нескольких промежуточных путей. Таким образом, имеется возможность улучшить пропускную способность базовой Дельта-системы. Для создания Дельта-системы можно использовать следующие способы построения [10.14, 10.17]:

• расширение звеньев;

• копирование Дельта-системы;

• введение дополнительных каскадов.

Первый способ состоит в организации многосвязной системы (рис. 10.17).

Второй способ иллюстрирует рис. 10.18. Система обеспечивает К независимых путей за счет введения К Дельта-систем. Такая система может стать неблокируемой, если К удовлетворяет следующему условию: К> n[SI2] + 1, где [ ] обозначают целую часть_числа-Рис. 10.17. Расширенная Дельта-система 8x8

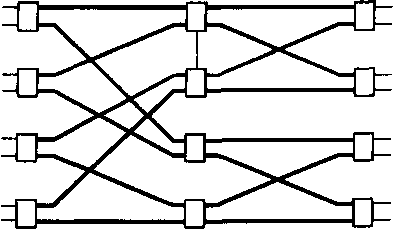
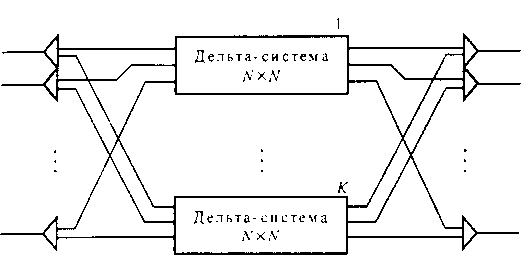
Рис. 10.18. Скопированная Дельта-система Третий способ состоит в добавлении новых, так называемых распределительных каскадов перед Дельта-системой, для того чтобы создавать альтернативные маршруты между парой вход-выход. Если добавляется К каскадов, то результирующее число промежуточных путей равно п^к.

Еще один способ построения можно получить при комбинировании двух последних способов. Он применяется в так называемой Параллельной Дельта-системе, которая представлена на рис. 10.19.

Параллельная Дельта-система емкостью N х N может строиться как:

• Ь параллельных Дельта-систем, называемых уровнями;

• один дополнительный коммутационный каскад, составленный из КЭ емкостью пхп, который называется распределенным каскадом;

• два дополнительных каскада, называемых каскадами расширения и концентрации, соответственно.

Параллельная Дельта-система обеспечивает Р = п х Ь различных про-

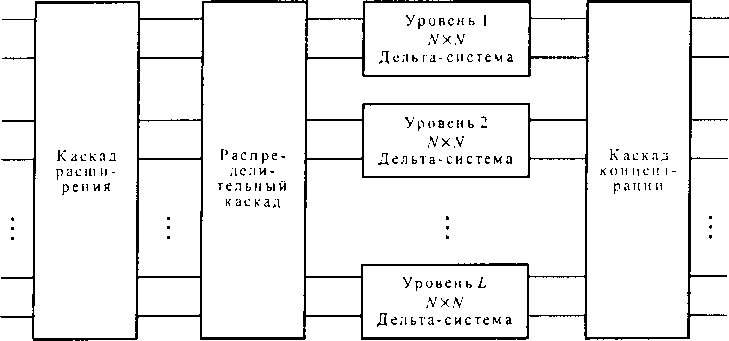
межуточных путей между каждой парой вход-выход. При этом система является неблокируемой, если число уровней Ь больше или равно где Б- число каскадов одного уровня.

Существуют и другие методы уменьшения или устранения блокировок, которые одинаково применимы как для КС с одним или несколькими промежуточными путями. К ним относятся:

• введение буферов на входах (выходах) КС и/или в каждом КЭ, что позволяет в случае блокировки поместить одну из двух ячеек в буфер, избежав тем самым ее потери;

• использование разных скоростей передачи в каждом каскаде КС [10.19]. Если скорость обработки в каждом последующем каскаде КС в два раза выше скорости обработки в предыдущем, то это позволяет устранить все внутренние блокировки в КС. Этот метод, однако, может потребовать неприемлемо высоких скоростей обработки информации при большом числе каскадов в КС.

⇐Коммутационная система типа кольцо | Мультисервисные телекоммуникационные сети | Сравнительный анализ вероятностных характеристик систем быстрой коммутации пакетов⇒