Так как рассмотренный выше метод оптимизации сети связи по критерию минимальной стоимости основан на ряде допущений, то он является приближенным. Оценим точность этого метода, следуя [8.5].

8.5.1. Основные допущения Число каналов на сети коммутации принято рассчитывать на основе критерия минимума капитальных затрат при фиксированном качестве обслуживания вызовов на пучках каналов пути последнего выбора (ППВ) и соблюдения требования кратности суммарного числа каналов в исходящем и входящем пучках прямых путей (ПП) числу каналов первичного модуля системы передачи [8.4]. Так, при использовании аналоговых систем передачи первичный модуль соответствует 12-ти каналам, цифровых систем пере дачи - 13-ти каналам. При соблюдении этих требований обычно принимают следующие упрощающие допущения:

1) пучки каналов являются полнодоступными и неблокируемыми;

2) функция капитальных затрат является непрерывной и дифференцируемой;

3) параметры оптимизационного уравнения зависят только от первого момента распределения нагрузки.

Данные допущения позволяют получить оптимизационные уравнения в сравнительно простом виде и эффективно их использовать при автоматизации проектирования информационной сети. Однако при этом возникает некоторая погрешность в определении емкости пучков, оценить которую аналитически достаточно трудно. Возникшую погрешность при использовании критериев [8.4] можно оценить косвенно, если провести оптимизацию сети с помощью методов, в которых отсутствуют указанные выше ограничения. В качестве таких методов можно использовать поисковые методы оптимизации, например, метод случайного поиска (МСП) [8.7], который часто эффективно применяют при анализе отдельных фрагментов сети без допущений, принятых в [8.4]. В дальнейшем оценку интересующей нас погрешности будем проводить именно с помощью этого метода. Сопоставив результаты оптимизации сети по двум методам, можно приблизительно оценить погрешность метода [8.4].

8.5.2. Выбор целевой функции при МСП

Под целевой функцией С будем понимать суммарные капитальные затраты на организацию сети связи:

где С/ - капитальные затраты на организацию одного канала 1-го направления; V, - емкость пучка каналов в 1-м направлении; 7^, - множество всех направлений.

Будем считать, что все пучки каналов ПП определяются таким образом, что сумма каналов в исходящем и входящем пучках между каждой парой узлов кратна принятому модулю первичной группы системы передачи М:

здесь к - множитель кратности (к 5* 0), причем распределение каналов по каждому из этих пучков осуществляется на основе обеспечения минимума суммарной избыточности нагрузки. Емкость пучков каналов обходных промежуточных путей (ОПП) также кратна М.

Пучки каналов ППВ являются пучками высокого качества и их можно определить с точностью до одного канала при вероятности потерь Р = 0,01. На пучки каналов ОПП поступают непуассоновские избыточные нагрузки, которые будем задавать их первыми двумя моментами распределения - математическим ожиданием интенсивности нагрузки Л, и ее дисперсией ст,². Для удобства в дальнейшем будем использовать коэффициент дисперсии

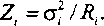
Целевая функция (8.27) при условии (8.28) была положена в основу при определении минимума капитальных затрат в методе [8.4]. При применении МСП целевую функцию (8.27) необходимо уточнить, связав емкость пучков К (г е Ы) с параметрами нагрузки, поступающей на этот пучок, вероятностью возникновения избыточной нагрузки и структурой узла коммутации. Влияние структуры узла коммутации на V, будем учитывать с помощью формулы

где символ Е(\ *, •) означает третью формулу Эрланга; Р - вероятность возникновения избыточной нагрузки, V, - емкость пучка каналов; Я, - интенсивность нагрузки, поступающей на этот пучок; й^, э, - эффективная доступность в направлении искания; Е, - коэффициент дисперсии поступающей нагрузки.

Эффективная доступность с/?, связана с емкостью пучка каналов коэффициентом доступности [8.3]

Исследованиями, проведенными в [8.3], установлено, что при существующих нормах на качество обслуживания коэффициент доступности можно принять 0,8 < < 1.

Чтобы воспользоваться формулой (8.29), необходимо знать параметры нагрузки, поступающей на пучок У_іу- пару 2,. Будем считать, что нагрузки, поступающие на этот пучок, независимы. Тогда

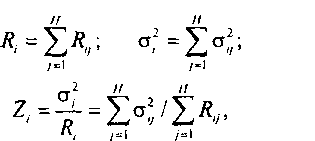
где /?у, - математическое ожидание и дисперсия нагрузки, поступающей в направлении / от направления у (/, у = 1, Н ) соответственно.

Задача отыскания параметров непуассоновской нагрузки, поступающей на блокируемые пучки каналов, до сих пор не нашла строгого решения. Приближенное решение этой задачи дано в разд. 6.3. В соответствии с результатами разд. 6.3:

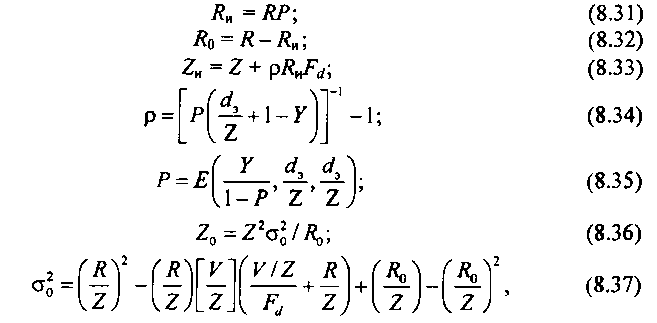
где Я, 2 - параметры нагрузки, поступающей на некоторое направление искания; Яо, 2_й- параметры нагрузки, обслуженной этим направлением; Я_т2_Я- параметры нагрузки, не обслуженной рассматриваемым направлением и передаваемой на дообслуживание на обходное направление связи.

⇐Оптимизация пучков каналов при неординарных пуассоновских потоках на пучках пути первого выбора | Мультисервисные телекоммуникационные сети | Алгоритм оптимизации целевой функции⇒