Как следует из предыдущего раздела, для определения вероятности потерь вызовов отдельных источников нагрузки предварительно требуется определить средневзвешенную вероятность потерь.

Рассмотрим задачу определения средневзвешенной вероятности потерь в направлении связи с использованием 2-аппроксимации [6.1, 6.3].

Рассмотрим аппроксимацию, позволяющую проводить расчет потерь в КС, на отдельные направления которой поступает избыточная нагрузка с параметрами Ли а²непосредственно по методу раздельных потерь (МРП). Особенностью этой модели является то, что она дает возможность, с одной стороны, достаточно хорошо учесть структуру КС и характер избыточной нагрузки, а с другой, - не приводит к большому объему вычислений. Эта аппроксимация является естественным обобщением аппроксимации Хейворда [6.3], который показал, что вероятность потерь вызовов на полнодос тупном пучке каналов, обслуживающем избыточную нагрузку (Л, а²), мож но приближенно оценить с помощью первой формулы Эрланга:

Вызовы, не обслуженные некоторой подсистемой (У, £/,), дообслужи-ваются бесконечномерным пучком, сопряженным с этой подсистемой. Нагрузка (Я, 7!), поступающая на неполнодоступный пучок, с помощью распределителя делится между подсистемами. Будем считать, что распределитель нагрузки работает так, что выполняются следующие требования [6.3]:

1) в статистическом отношении все подсистемы должны быть эквивалентны;

2) вызов не должен поступать на некоторую подсистему, не имеющую возможности его обслужить, если имеются подсистемы, которые могут это сделать;

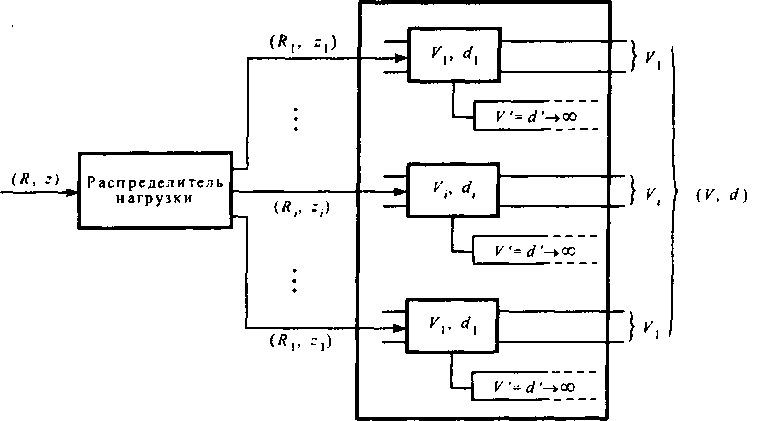
Рис. 6.1. Декомпозиция неполнодоступного пучка 3) если вызов поступает в такой момент, когда он не может быть обслужен ни одной из подсистем, то он обслуживается бесконечномерным пучком каналов такой подсистемы, при которой выполняется требование 1.

Следствием этих требований является то, что вероятность потерь в любой подсистеме будет совпадать с вероятностью потерь в системе, на которую поступает нагрузка (Я, 2). Другими словами, расчет вероятности потерь в системе можно свести к расчету вероятности потерь в подсистеме.

Дисперсию а, числа занятых каналов в системе можно выразить через дисперсии о] з числа занятых каналов подсистем и их коэффициенты корреляции р,Если считать, что условия 1-3 выполнены, то

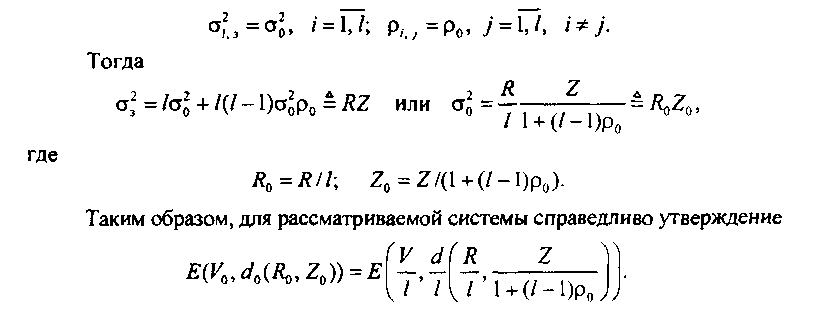
Очевидно, чтобы расчет вероятности потерь свелся к расчету вероятности потерь при нагрузке, определяемой первыми двумя моментами ее распределения, необходимо соблюдение равенства 2о = 1 или 2/[ 1 + (/ - 1)] = 1, что соответствует разбиению исходной системы на подсистемы, число которых определяется по формуле 1 = (2- 1 + ро)/роИзвестно такое правило работы распределителя нагрузки [6.3], которое, с одной стороны, удовлетворяет требованиям 1-3, а с другой, - позволяет максимизировать коэффициент корреляции ро, не изменяя при этом вероятности потерь. Это правило состоит в следующем. Из всех подсистем, в которых имеется возможность обслужить, по крайней мере, один вызов, последний должен предлагаться такой подсистеме, в которой бесконечномерный пучок содержит наименьшее число занятых каналов. Полагая, что Ро = 1, получаем I ~ 2. Эго приводит к аппроксимации, позволяющей рассчитывать вероятности потерь в многозвенных КС, на отдельные направления которой поступает нагрузка с параметрами (Я, 2) по формуле (6.14).

Применение (6.14) для приближенной оценки вероятности потерь в обходном направлении приводит к необходимости проведения расчетов, когда емкости фиктивного пучка У/2 и фиктивной доступности <И2 являются нецелыми числами. Если емкость пучка и доступность не являются целыми числами, а для расчетов применяется ЭВМ, то вычисления можно провести по простым рекуррентным формулам.

Остановимся более подробно на алгоритме вычислений вероятности потерь, когда Уи с! - нецелые числа. В этом случае вероятность потерь

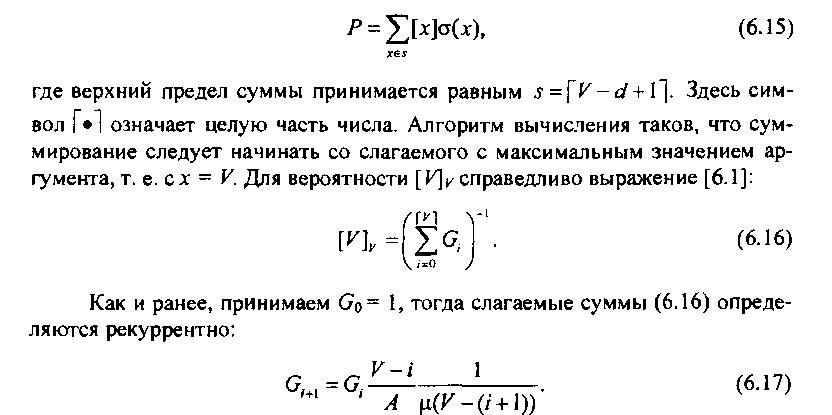
Вероятность [х- 1] находится также рекуррентно:

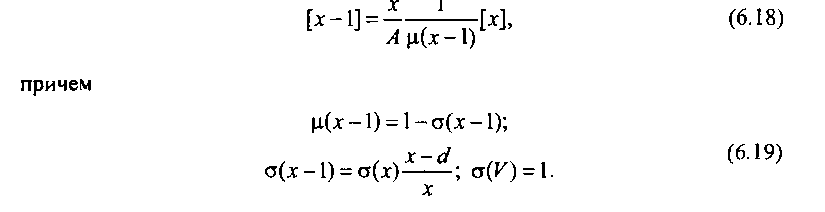
Отметим, что если V и с/ - целые числа, то результаты расчета по (6.15) совпадают с результатами расчета по формуле Эрланга для идеального неполнодоступного включения.

⇐Аналитические модели для описания нагрузки и потерь | Мультисервисные телекоммуникационные сети | Параметры избыточной и обслуженной нагрузок в направлениях связи системы многоканальной коммутации⇒