В сети с обходными направлениями типа, представленной на рис. 8.1, в соответствии со схемой выбора обходных путей (см. рис. 8.2), можно выделить две характерные ситуации, к которым сводятся все возможные случаи выбора обходных путей.

1. Нагрузка, которую необходимо обслужить между исходной станцией и станцией назначения, поступает сначала на прямой путь (СЛ, непосредственно соединяющая станции). Если на данном пути поступающая нагрузка не может быть обслужена с требуемым качеством обслуживания, то избыточная нагрузка с прямого пути поступает на дообслуживание на обходной путь (рис. 8.3).

2. Для нагрузки, не обслуженной в ситуации п.1, выбирается следующий обходной путь с большим числом транзитных УК (рис. 8.4).

Таким образом, при разработке метода оптимизации сети по выбранному критерию рассматривают две базовые сетевые структуры: 3-узловую сеть (см. рис. 8.3) и 4-узловую сеть (см. рис. 8.4). Кроме того, рассматриваемый метод основан на следующих понятиях, введенных впервые в работе [8.15]:

- маргинальное использование Н, определяющее приращение обслуженной нагрузки Ло при единичном увеличении емкости пучка каналов N и постоянном значении поступающей нагрузки А (в этом случае: г = /(А, И) - избыточная нагрузка, А₀=А-г - обслуженная нагрузка): я = =-(-*') ;

V ]_/1_=СОП5г ч ОМ у л.сог^

- маргинальная емкость р, определяющая приращение поступающей нагрузки при единичном увеличении емкости пучка в условиях постоянных потерь Е на этом пучке:

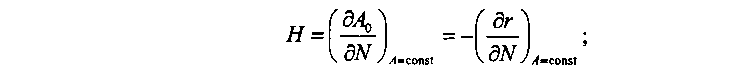
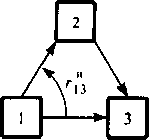
Рис. 8.3. Организация обходов на одно- Рис. 8.4. Организация обходов на однонаправленной трехузловой сети направленной четырехузловой сети

- маргинальная избыточная нагрузка у, определяющая интенсивность изменения избыточной нагрузки при изменении поступающей нагрузки и постоянной емкости пучка:

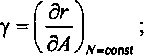
- маргинальная поступающая нагрузка ср, определяющая приращение поступающей нагрузки при единичном увеличении емкости пучка и постоянном значении избыточной нагрузки:

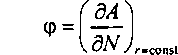
При определении перечисленных величин предполагается, что емкости пучков каналов в пути могут быть нецелочисленными.

Для простейшей базовой сетевой структуры (см. рис. 8.3) оптимизируемая функция стоимости

В этом случае стоимость С является функцией только одной переменной Ы\, так как при задании М можно определить параметры нагрузки, поступающей на путь последнего выбора, а затем определить емкости тУ₂и в соответствии с заданной величиной потерь на этом пути - Таким образом, для определения оптимального значения функции (8.1) необходимо решить следующее уравнение (при заданных нагрузке А_ипоступающей на пучок каналов N1 пути первого выбора; потерях на пучке каналов N2 - Е₂= / дал и пучке каналов N3 -Е] = Рдоп пути последнего выбора):

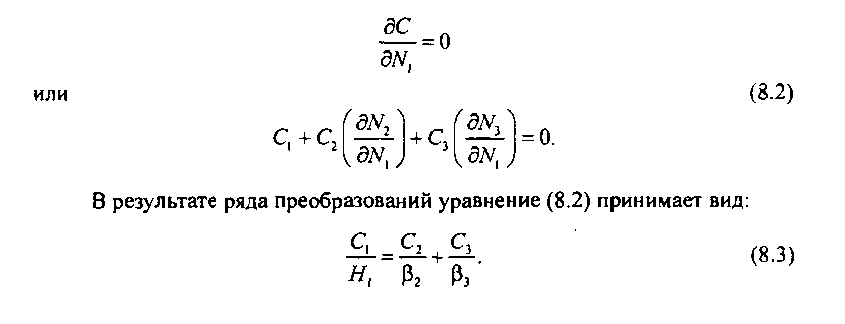
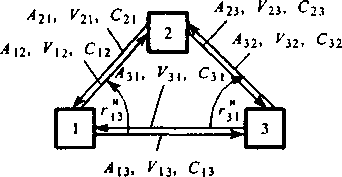
Рис. 8.5. Организация обходов на двунаправленной 3-узловой сети: А и, - нагрузки, которые должны быть обслужены между узлами 1 и 3, 3 и 1 соответственно; Vи, V_y„ V_2i, V_}2, У,2, V₂\ - емкости соответствующих пучков каналов; С[j = С21, Сз ~ C31, С23⁼С32 - стоимости одного канала соответствующих CJ1

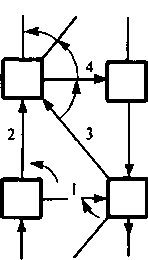
Рис. 8.6. Организация обходов на фрагменте иерархической сети:

1 - пучок каналов, входящий в один из путей высокого использования; 2 - пучок каналов обходного пути; 3-4 - пучки каналов в следующих обходных путях высокого использования

где п, т - приращение числа каналов в СЛ между узлами (3,1) и узлами (1,3) соответственно. Если наращивание СЛ между этими узлами проводится блоками определенной емкости А/, то {т + и) = М.

Из оптимизационного уравнения (8.6) для базовой структуры в виде ориентированной 3-узловой сети можно получить как частные случаи все известные критерии оптимизации для подобных базовых структур, что говорит о достаточной его общности.

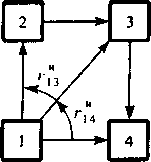
В работах [8.15, 8.16] показано, что описанный выше принцип построения оптимизационных уравнений для 3-узловой базовой структуры может быть распространен и на более сложные структуры, фрагмент которой, например, представлен на рис. 8.6.

Если обозначить стоимость СЛ, составляющих обходные пути, находящиеся ниже пучка каналов 1, С' а СЛ, составляющих пути, находящиеся выше пучка каналов 3, С", то функция стоимости приведенного фрагмента сети будет иметь вид:

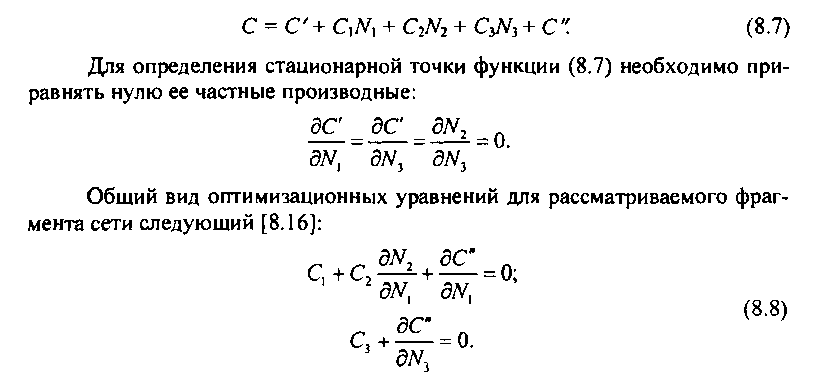
Таким образом, в работе [8.16] показано, что критерий минимума стоимости для 3-узловой базовой сетевой структуры с достаточной степенью точности можно применить для любого пути высокого использования в сети большей размерности.

При составлении и решении оптимизационных уравнений необходимо особое внимание уделить выбору соответствующих аппроксимаций, применение которых позволяет обеспечить допустимую точность вычислений и в то же время сократить их число и трудоемкость переборов. Так, например, в [8.12] предложена система оптимизационных уравнений для 4-узловой базовой сетевой структуры (см. рис. 8.4), где данная базовая структура рассматривается как декомпозиция двух 3-узловых базовых структур, связанных определенной функциональной зависимостью:

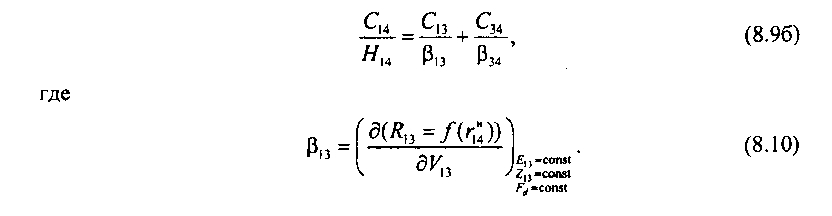
Здесь Л₁₃= (Ли + /;") - интенсивность нагрузки, поступающей на пучок каналов между узлами (1,3); - коэффициент дисперсии нагрузки на данном пучке; г"₄- избыточная нагрузка с пучка каналов между узлами (1,4); Ра - коэффициент доступности к пучку У\₃; Е\з - потери на пучке К₃, полученные после определения оптимального значения емкости пучка Таким образом, функциональная зависимость между уравнениями (8.9а) и (8.96) определяется двумя выражениями:

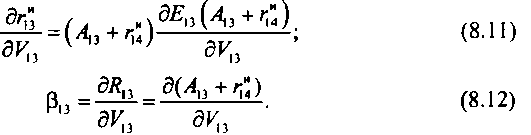
где Кіз - определяется из оптимизационного уравнения (8.9а).

⇐Постановка задачи | Мультисервисные телекоммуникационные сети | Решение базовых оптимизационных уравнений⇒