Как было показано в разделе 3.2, для определения эффективной доступности необходимо знание математического ожидания доступности, ее дисперсии и начальных моментов. Если требуется получить приближение К-го порядка, то для определения ЭД необходимо знание К первых начальных моментов. Так, в случае приближения второго порядка, как следует из (3.11), необходимо знать математическое ожидание доступности и ее дисперсию. Вопрос о математическом ожидании доступности был подробно рассмотрен в разделе 3.2.

Определим дисперсию доступности. Рассмотрим случай, когда УХ« К- Это соотношение выполняется в КС при достаточно большом числе направлений или относительно малом размере коммутаторов первого звена и справедливо для реальных систем. Как следует из раздела 3.2, математическое ожидание доступности в этом случае имеет вид

и может рассматриваться как сумма математических ожиданий двух случайных величин: доступности 8, обусловленной наличием незаблокирован-ных выходов в направлении искания и доступности 5з, обусловленной наличием заблокированных выходов направления, которые в рассматриваемый период времени могут быть разблокированы и, следовательно, стать доступными для рассматриваемого входа. Очевидно, что

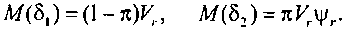
Ранее при выводе формулы математического ожидания доступности КС предполагалось, что состояние доступности выхода не зависит от состояний доступности других выходов пучка, т. е. предполагалось, что число доступных каналов подчиняется биноминальному распределению. При этом предположении дисперсии случайных величин б, и 82 будут равны соответственно:

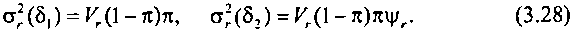
Дисперсия числа доступных каналов в направлении искания определится в виде

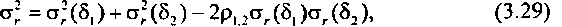
где Р1.2 - коэффициент корреляции.

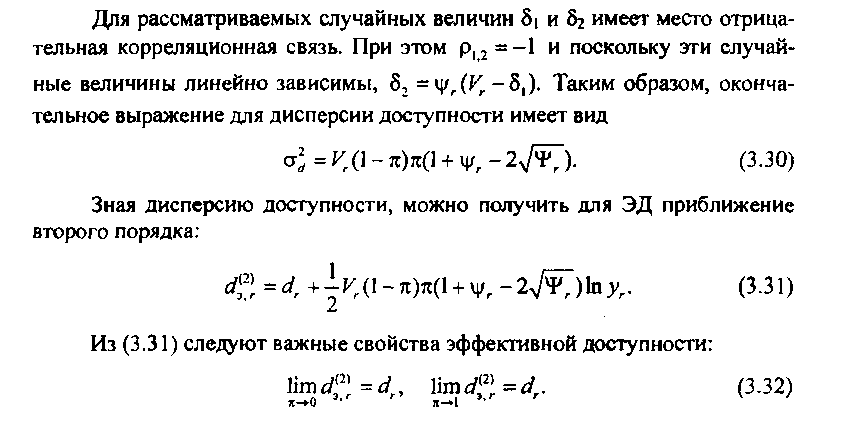
Эти предельные соотношения важны для понимания того, когда ЭД можно аппроксимировать средней доступностью.

Для получения приближения третьего порядка необходимо найти три первых слагаемых (3.12), которые выражаются через три первых начальных момента доступности. Поскольку в рассматриваемом случае величина 5 представляется в виде суммы двух случайных величин 8 и 8₂, то в соответствии с правилом вычисления моментов

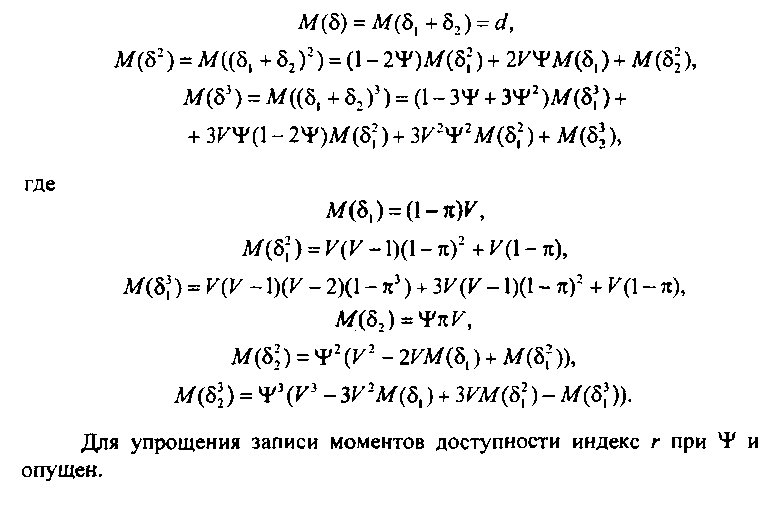
Приведенные формулы начальных моментов доступности позволяют представить ЭД как приближение третьего порядка.

Анализируя приведенные формулы ЭД, полученные при аппроксимации ее приближениями 1-го порядка (/ = 1, 2, 3), видно, что все аппроксимации являются функциями вероятности блокировки выхода л. Кроме того, аппроксимации ЭД при I > 1 зависят от использования канала в пучке рассматриваемого направления искания. При фиксированной вероятности п эффективная доступность уменьшается с уменьшением использования канала (удельной обслуженной нагрузки у_г). Выше показано, что для КС заданной структуры вероятность к зависит от нагрузки, обслуженной этой системой. Если вероятность потерь в системе нормирована, то нормированной является и допустимая обслуженная нагрузка, а, следовательно, и вероятность блокировки выхода п. При существующих нормах на качество обслуживания абонентов вероятность п для квазиэлектронных и электронных КС обычно не превышает 0,2. Если учесть, что удельная нагрузка на пучок каналов в рассматриваемом направлении искания у,- обычно выбирается исходя из требования экономичного построения сети связи и составляет Уг > 0,3 Эрл, то можно оценить пределы изменений эффективной доступности при выборе для нее различных аппроксимаций. Так, например, при выборе в качестве ЭД приближения второго порядка отклонение бГ‘²⁾от в случае КС достаточно большой емкости (£ = оо) составит

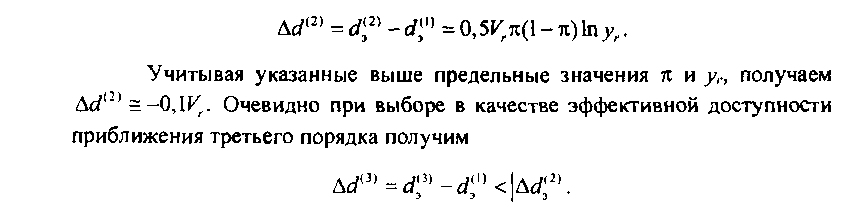
Таким образом, влияние второго и третьего слагаемых в формуле ЭД (3.12) оказывается заметным лишь в области сравнительно малых значений удельной обслуженной нагрузки у_г. Проведенное численное исследование аппроксимации ЭД приближениями первого, второго и третьего порядков для многозвенных КС, характеризующихся различной структурой, показало, что, если 0,3 < у, < 0,6 и я < 0,2, то при выборе приближения второго порядка ЭД отличается от математического ожидания доступности менее чем на 10 %. При у_г< 0,6 и использовании ЭД как приближения второго порядка отклонение от математического ожидания доступности не превышает 3 %. Это означает, что если у_г< 0,3 и 0,2, то при проведении инженер-

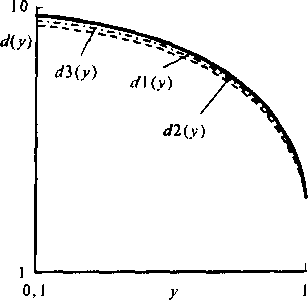
Рис. 3.1. Зависимость изменения приближений ЭД от использования пучка каналов: с/1 Су) - приближение первого порядка; сП{у) - приближение второго порядка; Л (у) - приближение третьего порядка ных расчетов для определения ЭД достаточно ограничиться приближением второго порядка. При я > 0,2 в области малых значений у_гжелательно аппроксимировать ЭД приближением третьего порядка. О влиянии порядка приближения на величину ЭД можно судить по графикам зависимости =/{у_г) (/ = 1,3), приведенным на рис. 3.1, для двухзвенной КС:

⇐Средняя доступность многозвенных кс | Мультисервисные телекоммуникационные сети | Коэффициент доступности кс и его свойства⇒