В разделе 3.1 было показано, что при достаточно высоком использовании каналов пучка направления искания средняя доступность является асимптотической оценкой ЭД. Из (3.11) также следует, что средняя доступность есть приближение первого порядка для ЭД. И, наконец, знание средней доступности необходимо также в случае, когда ЭД аппроксимируется приближениями более высоких порядков.

Учитывая эти обстоятельства, рассмотрим вопрос о величине средней доступности в однородной многозвенной КС [3.1, 3.2].

Пусть в некотором состоянии {х} фиксированного коммутатора первого звена возник вызов, требующий с вероятностью т^(г = 1, И) соединения с выходом заданного направления г, содержащего У_гвыходов. В этом состоянии рассматриваемого коммутатора среди соединений имеется в среднем т1_гдс соединений, установленных в рассматриваемом направлении [3.5, 3.9]. Оставшиеся £,(х) = [У_г-ц_гх] выходы направления могут быть использованы для установления соединения, если они свободны и доступны входу, по которому поступил вызов. Квадратные скобки в выражении для %(х) означают, что £(*) выбирается ближайшим целым к V,. -т_гх. Выход исходящего пучка будем считать доступным фиксированному входу, если он является незаблокированным, т. е. может быть достигнут для опробования на сво-бодность (или занятость) или для установления соединения.

При определении числа доступных выходов предположим, что состояние доступности каждого выхода является равновероятным и независимым от соответствующих состояний других выходов. При таком допущении можно считать, что в состоянии {х} вероятность того, что для фиксированного входа окажутся доступными j линий (0 < у < %(х)), подчиняются распределению Бернулли, т. е.

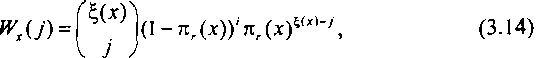
где 71_г(х) - вероятность блокировки (недоступности) отдельного выхода направления в состоянии {х}.

Математическое ожидание числа незаблокированных и, следовательно, доступных выходов в состоянии {х} равно

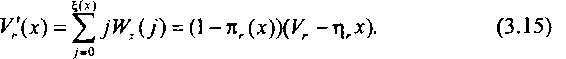
Математическое ожидание числа заблокированных, т. е. недоступных выходов в этом же состоянии

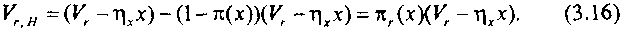
Введем понятие нагрузочной группы КС. Под нагрузочной группой будем понимать такое максимальное число входов КС (при фиксированном числе ее выходов), при котором эта система остается еще неблокируемой. Пусть рассматриваемая КС содержит g нагрузочных групп. Недоступные заблокированные выходы становятся доступными фиксированному входу рассматриваемой нагрузочной группы по мере их разблокирования. Однако эти выходы могут оказаться доступными и другим нагрузочным группам. Обозначим через у, долю выходов, которые окажутся доступными рассматриваемой нагрузочной фуппе. Если считать, что в КС нагрузочные группы идентичны в отношении их размера и создаваемой ими нагрузки, то можно принять v/_r= l/g и считать, что из всех заблокированных выходов число выходов, доступных нагрузочной фуппе по мере их разблокирования, будет равно

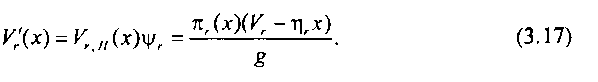
Доступность с1_г(х) в состоянии {х} будет определяться всей совокупностью доступных каналов в этом состоянии, т. е.

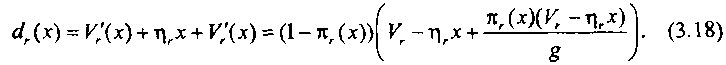
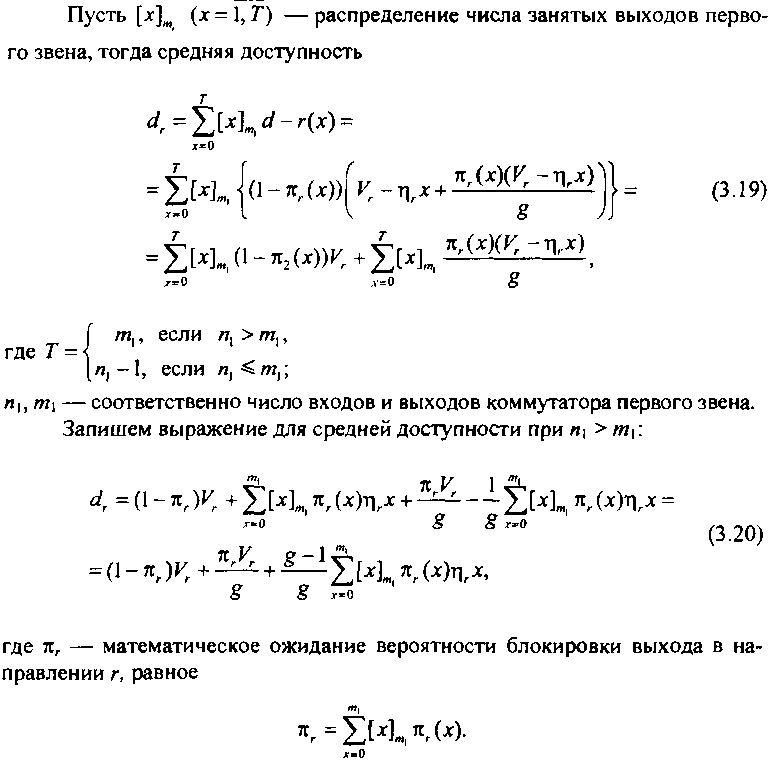
Для КС заданной структуры точное значение я(х) для стационарного режима работы системы можно найти из решения уравнений марковского случайного процесса с непрерывным временем и конечным числом состояний. Однако для реальных КС определение точного значения л_г(х) не представляется возможным из-за существенно большой размерности пространства состояний процесса. В ряде случаев я, (х) может быть найдено приближенно. Но даже при приближенном описании п, (х) выражение средней доступности оказывается сложным и требует значительного объема вычислений. Поэтому в целях упрощения выражения для <1_Гперейдем от я, (х) к ее математическому ожиданию я,.. Учитывая сказанное, выражение (3.20) может быть преобразовано к виду

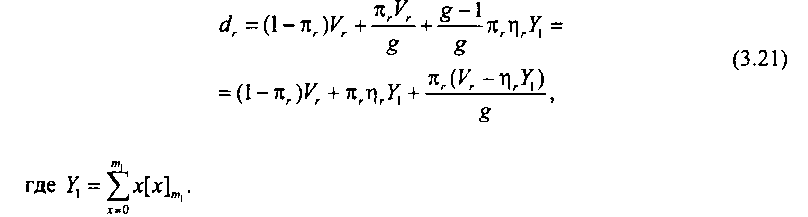
Рассмотрим случай, когда щ ^ т_х. Переходя в (3.19) от п_г(х) к л„ получаем

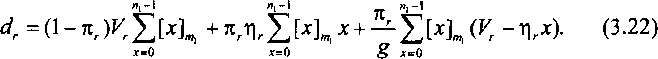
Пусть [х]_п- вероятность занятия х произвольных входов в коммутаторе первого звена. При п\ < т\ распределение [х]_Пможно аппроксимировать распределением Бернулли [3.5, 3.9]:

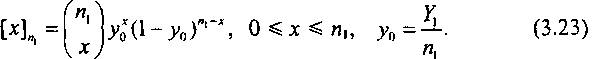
Поскольку на рассматриваемый коммутатор первого звена вызовы могут поступать тогда, когда в нем имеется по крайней мере один свободный вход, то для вычисления математического ожидания доступности КС при п\ ^ т\ необходимо от заданного распределения [х]_пчисла занятых выходов перейти к распределению [х]* числа занятых входов, определенному на множестве состояний: {0}, {1}, …, {л, - 1}.

Распределения [х]* ., и [х]_ясвязаны между собой следующим соотношением:

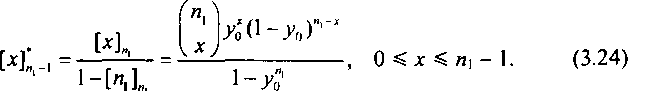
Подставив (3.24) в (3.22), получим

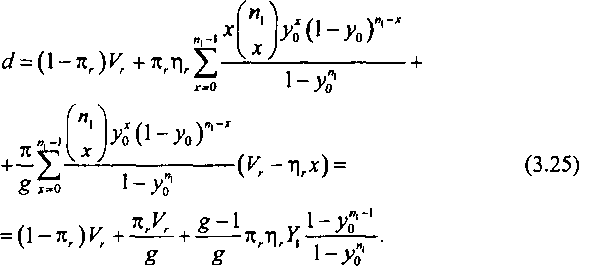
Окончательно для средней доступности имеем

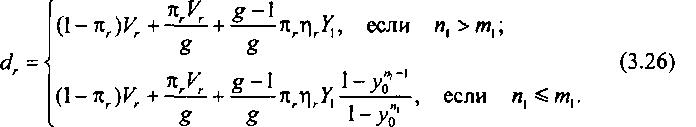
г Из (3.26) следует, что для расчета (У,-, кроме структурных и нагрузочных параметров, необходимо знание вероятности к_г. Так как к,- есть средняя вероятность блокировки некоторого фиксированного выхода рассматриваемого направления г по отношению ко входу, на который поступил вызов, то эту вероятность можно трактовать как вероятность потерь по времени в КС, работающей в режиме индивидуального искания. Поэтому для нахождения вероятности л,, можно применить известные методы расчета потерь по времени. В дальнейшем для пояснения сущности проблемы и иллюстрации связи предлагаемого метода расчета доступности с известными методами для определения к_гвоспользуемся методом вероятностных графов, который был рассмотрен в гл. 2.

Проведенное сравнение изложенного метода определения эффективной доступности с другими методами показало [3.2], что известные формулы определения средней и эффективной доступности могут быть выведены из полученных в этой главе выражений при введении ряда определенных физических ограничений. Это обстоятельство говорит о том, что полученные выше выражения для средней и эффективной доступности носят достаточно общий характер и позволяют проводить расчет КС в случаях, когда другие методы оказываются неприемлемыми и прежде всего в КС узлов ЦСИС.

⇐Асимптотическая оценка эффективной доступности | Мультисервисные телекоммуникационные сети | Дисперсия и начальные моменты распределения доступности⇒