Целевые функции, представляющие интерес для практики, являются, как правило, недифференцируемыми и часто многоэкстремальными функциями. Для их оптимизации используют методы математического программирования, например, дискретные аналоги градиентного метода, метода оврагов и др. [5.5]. Однако, когда единственно доступной информацией о ЦФ является лишь ее значение в некоторой точке, то для оптимизации ЦФ используют поисковые методы [5.3, 5.5]. Поисковые методы, в которых очередной шаг осуществляется рандомизированно, получили название методов случайного поиска (МСП) [5.5].

Остановимся более подробно на одном МСП, в котором выбор координат точки О осуществляется рандомизированно, причем рандомизация ставится в зависимость от «успеха» поиска и осуществляется за счет введения штрафных функций (ШФ). Это так называемые обучающиеся или стохастические автоматы (СА) [5.4, 5.5]. Особенностью методов управления на основе СА является то, что они не используют априорную информацию о функционировании объекта управления, а учитывают лишь характер изменения ЦФ. Это определяет медленную сходимость алгоритмов оптимизации, основанных на ШФ для плохо обусловленных функций [5.5]. Кроме того, в [5.12] отмечается, что СА применимы только в условиях стационарности. Тем не менее в ряде работ, например [5.2, 5.13], предлагается использовать СА для управления на сетях связи. Учитывая важность эффективного управления КР на ЦСИС при введении РКР, представляется необходимым при выборе концепции управления КО на узлах с РКР оценить целесообразность применения СА как альтернативы управления РКР на основе модель ных методов, учитывая при этом скорость сходимости, устойчивость решения, затраты на оптимизацию.

Исследуем два подхода к решению задачи управления РКР: первый основан на измерении параметров случайной среды и использовании аналитических моделей объекта управления, второй - на применении СА. Однако предварительно рассмотрим вероятностные характеристики УК ЦСИС с канальным резервированием.

Целевые функции, используемые ниже, базируются на вероятностных характеристиках УК ЦСИС, таких, как вероятность потерь из-за внутренних блокировок, вероятность потерь из-за порогового ограничения, вероятность потерь из-за занятости пучка каналов. Эти характеристики для РКР при гетерогенной пуассоновской нагрузке и пороговом ограничении КР были подробно уже изучены в разд. 5.2.

где

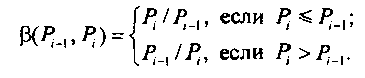
Если Р, = Р для всех г = 1, т, то 0\ = т - 1. Таким образом, задача выравнивания потерь сводится к одноразовому отысканию порогового вектора Г, при котором достигается максимум 0[. О характере ЦФ можно судить по графику рис. 5.10, на котором представлена функция 0\ =ЛТ) для пучка каналов V = 30 Рис. 5.10. Вид функции (5.22) в зависимости и двух классов пользователей, от изменения порогов Т\ и Т₂

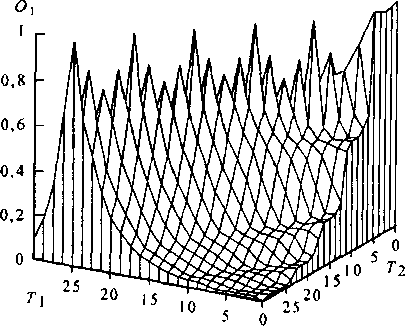
один из которых требует одноканального (М\ = 1), а второй - шестиканального ресурса (М₂= 6), причем А, = 10 и А₂= 1 Эрл.

Для оптимизации (5.22) был исследован ряд поисковых методов. Достаточно эффективным оказался МСП с возвращением в исходную точку при неудачном шаге и субградиентном переходе при удачном шаге [5.5]. Результаты оптимизации при У= 30, А \ = 10 и А₂= 1 Эрл представлены в табл. 5.3.

Из этой таблицы видно, что глобальный максимум (О■ = 1) был найден на 6-м рабочем шаге. При этом общее число шагов поиска равно 19. В результате оптимизации получены следующие значения порогов: Г, = 25, Т₂= = 30. Вероятности потерь вызовов каждого класса изменились с Р\ = 0,0153, Р₂= 0,0817 при Г, = Т_г= 30 наР₁-Р₇= 0,0588.

Таблица 5.3

Сходная задача при предположении о стационарности нагрузок была решена с помощью СА при выборе ШФ в соответствии с [5.2]. Так как метод СА - неаналитический, то для оценки его эффективности потребовалось имитационное моделирование. Имитационная модель реализует процесс размножения и гибели. Моделирование с целью быстрого набора статистики было выполнено для пучка емкостью V = 12 каналов и двух нагрузок: А , создаваемой одноканальными вызовами, и А₂, создаваемой шестиканальными вызовами, причем А₁= 7 и А 2 = 1 Эрл.

Точное решение, полученное по формулам разд. 5.2, дает Т\ = 7, Т₂- 12, при этом получаем Р\ = Р₂= = 0,544. Результаты имитационного моделирования представлены на рис. 5.11, где приведены зависимости изменения оценок вероятностей потерь Р\ и Р₂от числа поступивших вызовов. Узкая заштрихованная область на рис. 5.11 соответствует среднему числу вызовов, поступивших в час наибольших нагрузок (ЧНН).

Анализируя зависимости изменения вероятностей Р\ и Р₂от числа поступивших вызовов, можно

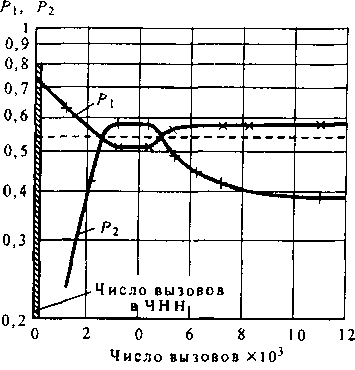
Рис. 5.11. Зависимость изменения оценок вероятностей потерь Р] и Р₂от числа поступивших вызовов констатировать, что на всем протяжении ЧНН при использовании СА не наблюдается выравнивания качества обслуживания, даже в области экстремально высоких потерь (Р\ = Рг = 0,544), когда статистика набирается достаточно быстро. Более того, метод СА не позволяет выравнить потери даже после поступления 12000 вызовов, что при среднем времени обслуживания вызова 3 мин соответствует по длительности примерно 55 ЧНН.

Сравнение результатов точных аналитических расчетов с данными имитационного моделирования работы системы управления на основе СА при стационарных нагрузках показывает:

1) для управления в реальном масштабе времени на УК ЦСИС с РКР метод СА не применим в силу недостаточной скорости сходимости;

2) штрафные функции [5.2] не являются точными соотношениями, что приводит к расхождению со строгими теоретическими результатами;

3) оценить затраты на оптимизацию при использовании СА не представляется возможным, так как за ЧНН СА не успевает выработать целесообразное поведение (т. е. улучшить целевую функцию).

Поскольку скорость сходимости к решению у СА в стационарном случае оказывается недопустимо медленной, то в нестационарных условиях использование СА тем более проблематично, и концепция управления КР должна строиться на измерении нагрузок, использовании аналитических моделей объекта управления и оптимизации ЦФ.

5.3.4. Динамическое управление распределением канальных ресурсов на основе резервирования при нестационарной нагрузке Рассматриваемый ниже метод динамического управления КР при нестационарной нагрузке в дальнейшем для краткости будем называть квази-стационарным методом управления (КУ). Идея КУ канальными ресурсами состоит в следующем. При КУ осуществляется периодическое измерение нагрузок на интервале 8, на котором нагрузки предполагаются стационарными. Управление КР осуществляется на основе результатов измерений нагрузок в конце каждого интервала 8 после оптимизации ЦФ. Принцип КУ иллюстрирует рис. 5.12, на котором показаны основные функциональные связи.

Если было бы возможно измерять мгновенные значения нагрузки, мгновенно вырабатывать параметры управления и на основе их управлять, то система КУ была бы фактически идеальной системой динамического управления. Наличие двух факторов - неточности измерения нагрузки и конечного времени оптимизации ЦФ - приводит к погрешности управления и в конечном счете снижает его эффективность по сравнению с идеальным случаем.

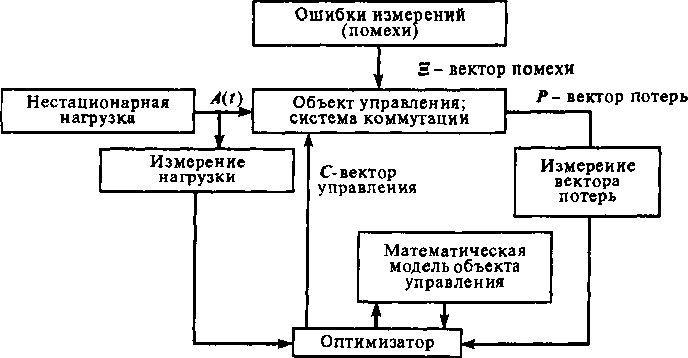
Рис. 5.12. Схема управления резервированием каналов на УК при нестационарной нагрузке

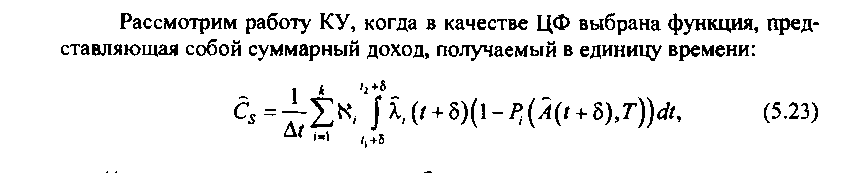
Рассмотрим работу КУ, когда в качестве ЦФ выбрана функция, представляющая собой суммарный доход, получаемый в единицу времени:

^ = Т-5>> I (' +'8)(1-^р, (^Я(‘ + Ь),Т))А, (5.23)

^Ы>»1 /, +5

где /ч*, - доход, получаемый при обслуживании одного вызова, поступившего от 1-го класса пользователей; Х,.(/ + 8) - оценка интенсивности потока вызовов, создаваемых 1-м классом пользователей в направлении связи; ^(А(( + 8), Г) - мгновенные потери г-го класса пользователей; Л(Г + 6) - оценка вектора нагрузки за время измерения Л = / - /2.

Заметим, что ЦФ (5.23) допускает и другие интерпретации. Если принять X, =1 (/ = 1, т), то (5.23) можно трактовать как суммарное число обслуженных заявок. При X, = V'¹ЦФ (5.23) будет соответствовать суммарной обслуженной нагрузке. О характере ЦФ в условиях стационарности можно судить по зависимости С₈от изменения порогов КР (рис. 5.13). График построен для случая двух классов пользователей - одноканальных (М\ = 1, А = 10 Эрл, (У - 1) и шести канальных (М₂= 6,^2= 1 Эрл, Лг⁼50).

Метод КУ был исследован на ряде примеров при различных нагрузках и величинах интервала 8 и X,. Однако ниже ограничимся иллюстрацией возможностей метода КУ на примере двух классов пользователей - одно- и шести канальных [5.14].

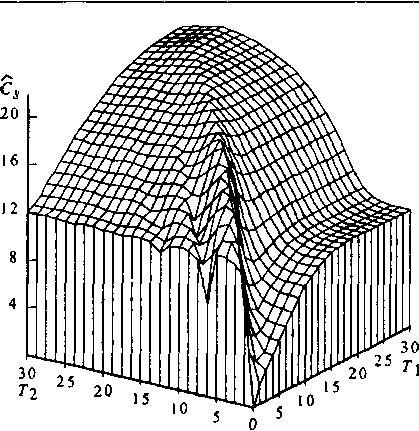
Рис. 5.13. Зависимость доходов С₅от изменения уровней резервирования обоих классов пользователей в случае преобладания одноканальных вызовов Предположим, что на УК поступают вызовы от двух классов пользователей, причем М₁= 1, Мг = 6. Они создают в направлении связи (V = 30) нагрузки А(/) и А₂((). Предположим, что они меняются во времени по следующему закону:

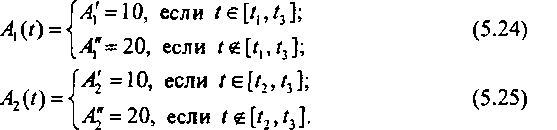
Изменение нагрузок совместно имитирует два пересекающихся ЧНН. Суммарная нагрузка представлена на рис. 5.14. Интервалы изменения нагрузок выбраны равными % = 30 мин. Среднее время обслуживания вызовов обоих классов было выбрано одинаковым и равным V"¹= 4 мин. Доход, получаемый от обслуживания вызова первого класса пользователей, принимался равным К = 1, а второго- Кг¹¹50 условных единиц.

При исследовании эффективности управления использовался анали-тико-имитационный подход, при котором измерения нагрузок проводились в процессе имитационного моделирования системы, а выбор параметров управления - на основе аналитической модели (раздел 5.3.4). Оптимизация

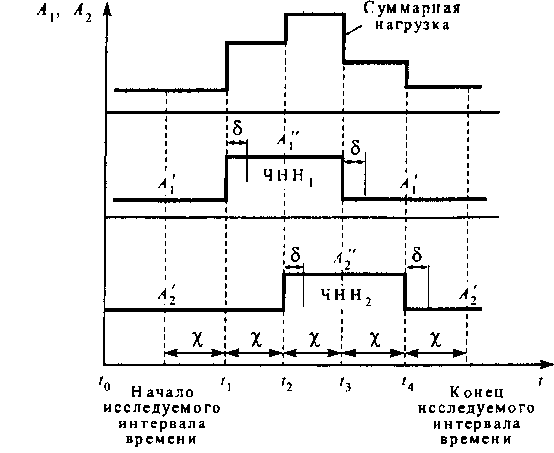
Рис. 5.14. Изменение интенсивностей нагрузок А \ иЛг в ЧНН

ЦФ (5.23) проводилась по полученным в результате измерений нагрузкам и заданным стоимостным коэффициентам К, при ограничении на вероятность индивидуальных потерь вызовов первого класса пользователей: Р\ < 0,05. Эффективность введения управления КР оценивалась по величине получаемого дохода в сравнении с тем, когда управление КР отсутствует.

Максимальный доход будет получен в том случае, если в процессе управления будут найдены такие значения порогов КР, при которых достигается максимум ЦФ. Для оптимизации ЦФ был использован субградиент-ный метод [5.5]. Измерение нагрузок осуществлялось методом сканирования. Интервал сканирования С, выбирался в соответствии с рекомендациями [5.6, 5.11, 5.14] и был принят равным одной минуте (^ = 0,25у~'). В качестве критерия эффективности использовалась величина дохода, приведенная к одной минуте. Время измерения нагрузки 8 изменялось от V^-1до 8у^_с интервалом в 0,5V^-’. Результаты аналитико-имитационного моделирования системы с КУ приведены в виде графика зависимости = /(8) на рис. 5.15. Как видно из графика, оптимальным временем измерения нагрузки является 8 = V¹. При этом доход за счет введения управления КР возрос на 13 %.

Рассмотренный метод динамического управления КР при нестационарных нагрузках, использующий принцип канального резервирования для отдельных классов пользователей, позволяет решать задачу динамического распределения канальных ресурсов в реальном времени в соответствии с

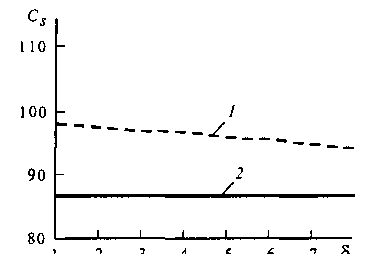
Рис. 5.15. Изменение величины дохода С, в зависимости от изменения времени измерения нагрузки для двух классов пользователей в случае преобладания одноканальных вызовов:

/ - при управлении КР; 2 - в отсутствии управления КР

выбранным критерием оптимальности.

Этот метод основан на измерении параметров случайной среды и использовании аналитической модели управляемого объекта - УК ЦСИС.

⇐Управление канальными ресурсами цсис на основе канального резервирования | Мультисервисные телекоммуникационные сети | Управление качеством обслуживания на основе резервирования канальных ресурсов на телефонных сетях⇒