При создании цифровых сетей с интеграцией служб особенно актуальным является вопрос об оптимальном распределении пучков каналов на такой сети. Применение точных аналитических моделей затруднено из-за сложной функциональной зависимости между вероятностью потерь и нагрузочными и структурными параметрами. Кроме того, применение строгих аналитических моделей требует большого объема вычислений, что ограничивает размеры анализируемой сети. Поэтому наиболее целесообразным представляется применение приближенных моделей, достоинство которых состоит в униформности вычисления характеристик и высоком быстродействии.
В гл. 6 был рассмотрен подход к расчету вероятностных характеристик систем коммутации при неординарных потоках, основанный на замене входящих маркированных пуассоновских потоков на эквивалентные по действию рекуррентные потоки. Исследования, проведенные в этом разделе, показали, что погрешность при такой замене в диапазоне нагрузок и потерь, встречающихся на практике, не превышает несколько процентов. Учитывая высокую точность такой аппроксимации и ее вычислительную эффективность, применим ее при оптимизации пучков каналов на цифровой сети с интеграцией служб.
Для иллюстрации предлагаемого подхода обратимся к однонаправленной трехузловой сети, представленной на рис. 8.3. Будем считать, что на пучке между узлами 1 и 3 имеет место совокупность К неординарных пуассоновских нагрузок, которые заменим на эквивалентные рекуррентные нагрузки (т. е. нагрузки, создаваемые рекуррентными потоками вызовов), задаваемые парой (Л,-, I,), / = 1, К. В этом случае рекуррентная нагрузка между узлами 1 и 3
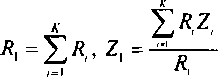
Таким образом, в отличие от постановки задачи оптимизации, рассмотренной в разд. 8.2, в данной постановке нагрузка между узлами I и 3 будет нагрузкой, создаваемой рекуррентным потоком, и задается парой (7?:, 1\). Характер собственных нагрузок между узлами 1-2 и 2-3 не имеет существенного значения, так как результирующие нагрузки между этими узлами, как правило, являются непуассоновскими. Для возможности сравнения результатов данного раздела с результатами, полученными в разд. 8.2 и 8.3, будем считать, что эти нагрузки являются пуассоновскими.
Итак, будем считать, что между узлами 1 и 3 имеет место собственная нагрузка (Л, 1\), между узлами 1 и 2 - собственная пуассоновская нагрузка А2, и между узлами 2 и 3 - собственная пуассоновская нагрузка-Аз (см. рис. 8.3).
Для оптимизации схемы, представленной на рис. 8.3, модифицируем уравнение Пратта [8.15]. В разд. 8.3 маргинальное использование вычислялось по формуле, в которой считались постоянными поступающая нагрузка А и коэффициент доступности :
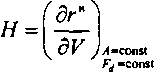
Теперь, в отличие от этой формулы, условие /l=const заменяется на условие R = const, Z = const, т. е.
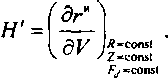
Таким образом, оптимизационное управление в случае 3-узловой сети, представленной на рис. 8.3, будет иметь вид
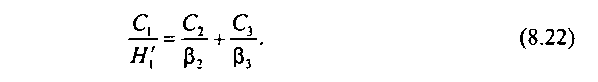
При использовании оптимизационного уравнения (8.22) алгоритм оптимизации 3-узловой сети, показанной на рис. 8.3, в целом совпадает с алгоритмом, рассмотренным в разд. 8.3. Отличие состоит лишь в процедуре определения емкости пучка каналов пути первого выбора V, по значению производной Из соотношения (8.22)

С другой стороны, значение этой производной можно приближенно определить в соответствии с подходом, предложенным в работе [8.13]
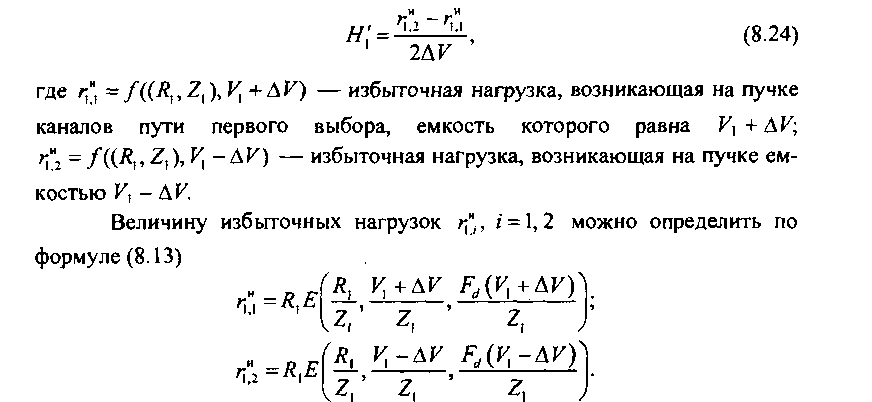
Так как определяется в соответствии с алгоритмом, описанным в разд. 8.3, из соотношения (8.23), то величину емкости V, пучка пути первого выбора можно найти итерационно из решения уравнения (8.24), которое в данном случае примет вид
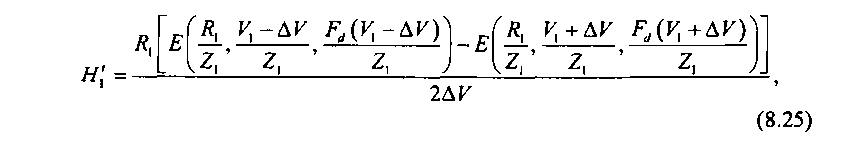
где AV = const и выбирается в соответствии с допустимой погрешностью вычислений.
Для определения значения V\ из уравнения (8.25) было использовано следующее итерационное уравнение:
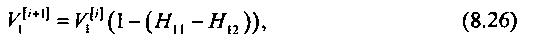
здесь #м= const и находится из соотношения (8.23), a#,2- из (8.25).
В качестве начального приближения для величины емкости пучка используем величину V,f0)= RtКак показали исследования, процесс является сходящимся осциллирующим. При этом число итераций при непосредственном использовании итерационного уравнения (8.26) не превышает 10-ти, а в случае ускорения сходимости не превышает 5-ти.
Рассмотренный алгоритм был проверен при решении задачи оптимизации однонаправленной 3-узловой сетевой структуры, для которой было получено предварительно точное решение. Влияние непуас-соновской нагрузки на характер оптимизации сравним на примере 3-узловой сети, для которой: А2= А3= 5 Эрл, С, = 1 и С2= С3= 1,5 у. е., /?1 = 5 Эрл, a Z\ = 1,2 или 4. Случай Z, = I подробно рассмотрен в разд. 8.3. Результаты оптимизации для трех значений Z\ сведены в табл. 8.1, в которой даны результаты оптимизации сети, полученные путем полного перебора. При оптимизации сети пучки каналов пути последнего выбора определялись при фиксированных средневзвешенных потерях в 1 %.
Как видно из анализа данных табл. 8.1, метод обобщенный на случай непуассоновских нагрузок дает результаты, близкие к оптимальным (погрешность не более 6 %). Увеличение коэффициента дисперсии Z, приводит к тому, что пучок каналов первого выбора при оптимизации будет иметь большую емкость при тех же условиях по сравнению со случаем, когда Z, = 1.
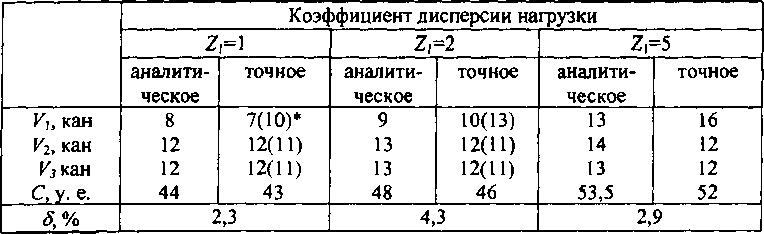
* В скобках приведен второй вариант решения.
Таким образом, рассмотренный выше алгоритм позволяет оптимизировать 3-узловые однонаправленные сети (см. рис. 8.3). Описанный подход распространяется на другие базовые сетевые структуры, рассмотренные в разд. 8.2 и 8.3. При применении этого подхода к этим структурам изменения будут касаться лишь определения пучков каналов путей высокого использования (ПП и обходной путь высокого использования). После того, как будет проведена оптимизация базовых сетевых структур и сети в целом, можно проводить детальный анализ качества обслуживания индивидуальных потоков вызовов, т. е. вычислять вероятности индивидуальных нагрузок (интенсивности и коэффициенты дисперсий).
⇐Решение базовых оптимизационных уравнений | Мультисервисные телекоммуникационные сети | Оценка точности метода оптимизации сети по критерию минимума капитальных затрат⇒
