Для вычисления вероятностных характеристик модели раздела 4.7 использовался итерационный метод Гаусса-Зейделя. Рассматриваемая система была исследована при следующих значениях структурных параметров: с повторными вызовами - у'і = 10,72 == 10, V = 10; без повторных вызовов - К =30.

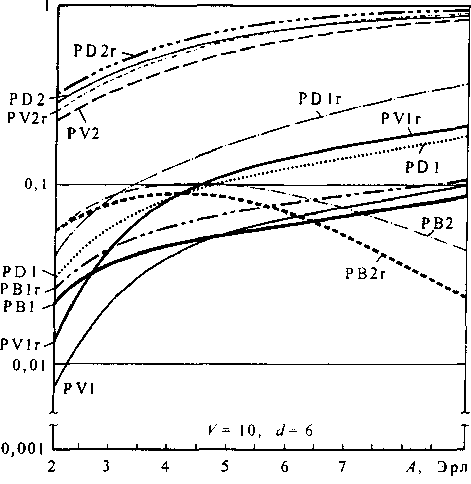
Рис. 4.11. Зависимости вероятностей потерь из-за блокировки на пучке п_У1, / = 1,2 (РУ1, РУ2, РУ1г, РУ2г), из-за внутренних блокировок п_ы, /=1,2 (РВ1, РВ2, РВ1г, РВ2г) и суммарных потерь я*, / = 1, 2 (Р01, Р02, Р01г, РБ2г) от изменения нагрузки при фиксированных емкости пучка и доступности без учета повторных вызовов и с их учетом. Зависимости со значком «г» относятся к системе с повторными вызовами

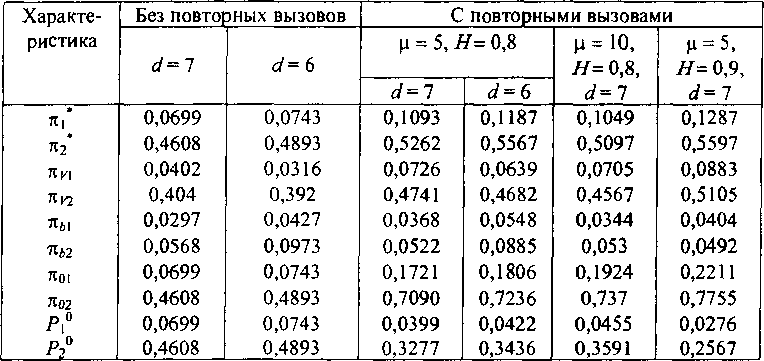
Представленные результаты численного исследования модели иллюстрируют влияние учета повторных вызовов в системах с многоканальной коммутацией, рассмотренной в предыдущих главах. С одной стороны, эти результаты, а их можно считать в известной степени точными, подтверждают выводы предшествующих глав, а с другой - демонстрируют степень изменения зависимостей вероятностей потерь от изменения нагрузки и от изменения доступности при учете повторных вызовов.

Рассмотренная математическая модель может служить основой для расчета звеньевых КС, а программу для ее численного исследования можно использовать для получения точных значений вероятностных характеристик при разработке приближенных способов расчета звеньевых КС и контроля при их статистическом моделировании.

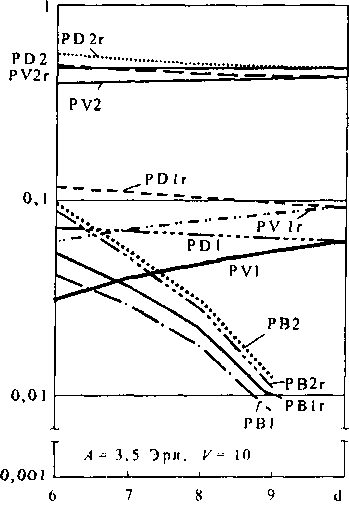
Рис. 4.12. Зависимости вероятностей потерь из-за блокировки на пучке (РУ1, РУ2, РУ1г, РУ2г), из-за внутренних блокировок (РВ1, РВ2, РВ1г, РВ2г) и суммарных потерь (РБ), РБ2, РБ1г, РБ2г) от изменения доступности при фиксированных значениях нагрузки и емкости пучка Литература 4.1. Ершова Э.Б., Ершов В.А. Цифровые системы распределения информации. М.: Радио и связь, 1983.

4.2. Ершов В.А., Игельник М.Б. Вероятностные характеристики модели идеального неполнодоступного включения при неординарном потоке вызовов // Электросвязь. №10, 1988. С. 48-50.

4.3. Ершов В.А., Игельник М.Б. Пропускная способность узла коммутации при ограничении ресурса устройства управления // Труды 5-й Всесоюзной школы-семинара по проблемам управления на сетях связи. М.: Наука, 1988. С. 86-89.

4.4. Ершов В.А., Игельник М.Б. Пропускная способность узла многоадресной коммутации // Труды 14-й Всесоюзной школы-семинара по вычислительным сетям. Ч. 1. Москва- Минск, 1989. С. 59-63.

4.5. Ершов В.А., Миронов А.А. Влияние межзвенных кроссировок на пропускную способность АМТСКЭ «Кварц» // Электросвязь. № 1, 1988. С. 26-29.

4.6. Корнышев Ю.Н., ФаньГ.Л. Теория распределения информации. М.: Радио и связь, 1985.

4.7. Степанов С.Н. Численные методы расчета систем с повторными вызовами. М.: Наука, 1983.

4.8. BotschD. Die Verlustwarcheinlichkeit einstufiger Koppelanordnungen der Vermittlungstechnik mit Extern and Intemverkehr // A.E.V., 1966. Vol. 22. N. 3.

4.9. Brockmeyer E., Hallstrom H.L., Jensen A. The Life and Works of A.K. Erlang. Acta Polytechnica Scandinavica Math. Copenhagen, 1948.

4.10. Ershov V., lgelnikM. A Grade of Service Analysis for Multi-Channel Switching in ISDN // ITC-13, Copenhagen, June 19-26,1991. P. 891-898.

4.11. Loize A., RoderA., ThiererG. Point-to-Point Loss in Case of Multiple Marking Attempts // University of Stuttgart, Institute of Switching and Data Technics, 1976.

4.12. Tabellen zu A.K. Erlangs Ifiterconnection Formel. Siemens & Halske Aktiengesellschaft, 1961,

4.13. Takagi K., Itoh M. Internal Blocking Probabilities of Eight-State Link Systems for Electronic Switching Systems // Review of the Electrical Comm. Laboratory, 1970. Vol. 18. N. 11.

Воланд: «…для того, чтобы управлять, нужно как-никак иметь точный план на некоторый, хоть сколько-нибудь приличный срок».

М.А. Булгаков «Мастер и Маргарита»

⇐Математическая модель узла коммутации цсис с учетом влияния повторных вызовов | Мультисервисные телекоммуникационные сети | Резервирование канальных ресурсов на цсис⇒