На цифровых сетях с интеграцией служб системы коммутации при обслуживании вызова в зависимости от вида информации должны коммутировать между собой одновременно т каналов, причем 1 < т < V, где V - число каналов в направлении связи. Выше было показано, что для определения вероятностных характеристик УК ЦСИС можно использовать модель идеального неполнодоступного включения, работающего в режиме многоканальной коммутации в сочетании с моделью эффективной доступности. Однако эта модель не учитывала влияния повторных вызовов, которые на практике при перегрузках могут иметь место.

Рассмотрим модель системы многоканальной коммутации с повторными вызовами, учитывающую возможность внутренних блокировок из-за неполной доступности каналов пучка. Схема функционирования модели представлена на рис. 4.10. На пучок из V линий с доступностью с/ < V поступают два пуассоновских потока первичных вызовов интенсивности X,-, / = 1, 2, и два соответствующих потока повторных вызовов от двух групп абонентов, повторяющих вызов. Каждый вызов (первичный или повторный) 1-го потока занимает ровно /„ / = 1, 2, (/) < /₂), свободных и доступных с некоторой условной вероятностью 0 < 0,(/, /₂) < 1, / = 1, 2, линий, где /) и /₂- число каналов, уже занятых обслуживанием вызовов первого и второго потоков соответственно И / + /₂= /, / < V. Если / < с/- /, ТО 0(/, /₂) - 1, и если / < с/- и, то 0₂(/, /г) = 1. Если 1> с!- 1\ или 1> с1- /₂, то 0 < 0,{/1, /₂) < 1, / = 1, 2. Условные вероятности доступности 0/(/, /г), » = 1, 2 в этом случае будут вычисляться по методике, изложенной в [4.7,4.10]. Если I > V- //, то 01 (/, /₂) = 0. Если / > V-/₂, то 0₂(/, /₂) = 0. Значения 0,{/,, /₂), /=1,2 вычисляются до реше-

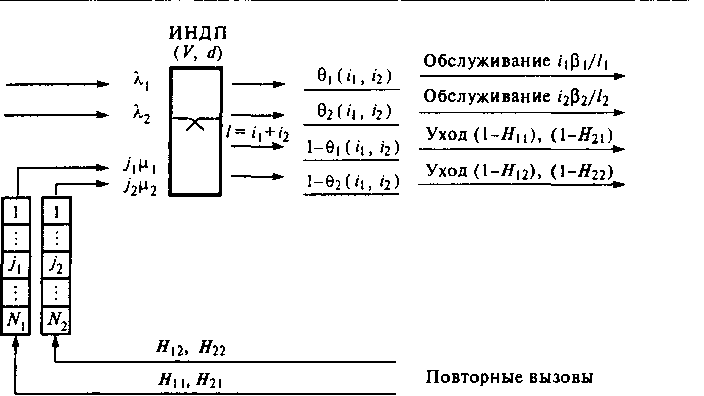
Рис. 4.10. Модель идеального иеполиодоступиого включения с многоканальной коммутацией и повторными вызовами иия системы уравнений равновесия. Поступивший (первичный или повторный) вызов 1-го потока с некоторой условной вероятностью потерь 1 - в,(/ь к), / = 1,2 получает отказ в обслуживании. В этой ситуации абонент с вероятностью Н\, < 1, г = 1,2, если это был первый отказ в обслуживании, и с вероятностью Н₂, < 1,/= 1,2, если это был повторный отказ, делает следующую попытку соединения через случайное время, имеющее экспоненциальное распределение с параметром, равным ц„ / = 1, 2, и с соответствующими дополнительными вероятностями (1 - Н_и), / = 1,2, или (1 - На), / = 1,2 покидает систему.

Обслуживание длится случайное время, имеющее экспоненциальное распределение с параметром Р„ / = 1, 2, и не зависит от типа вызова (первичный или повторный). По окончании обслуживания вызова освобождается одновременно ровно //,/=1,2 линий. Будем предполагать, что максимальное число абонентов, повторяющих вызов, ограничено целым числом N1, / = 1,2. Отсюда следует, что, получив отказ в обслуживании в первичной попытке при наличии Л/, / = 1,2 абонентов, повторяющих вызов, абонент с вероятностью единица покидает систему необслуженным.

Длительности обслуживания вызовов независимы между собой и от поступающих потоков первичных и повторных вызовов. Потоки первичных, а также потоки повторных вызовов от каждого повторяющего абонента взаимно независимы.

Модель описывается марковским процессом £,(/) = (/,(/), *1(0» Ш))>

/ > 0, с состояниями (/1,^2, /1, *2) £ если/,= 0, 1,…, N1 - число абонентов, повторяющих вызов в первой группе; 72 = 0, 1,Ы₂- число абонентов, повторяющих вызов во второй группе; / = 0, 2/,„. , [У/1{\1\ - число линий, занятых первичными вызовами первого потока или повторными вызовами первой группы; /₂= 0, к, 11₂, …, /Щг - число линий, занятых первич ными вызовами второго потока или повторными вызовами второй группы ([а] - целая часть числа а).

При условии выполнения свойства эргодичности (его выполнение зависит от значения / = 1,2, если //,< оо, / = 1,2, то свойство эргодичности выполняется всегда) для процесса ^(/) можно выписать систему уравнений равновесия. Обозначим через Р(/_Ьу'2, /'1, ь) стационарную вероятность нахождения марковского процесса £,(/) в состоянии (/,, у₂, й, Ь)- Тогда система уравнений равновесия, связывающая стационарные вероятности Н, к), имеет вид

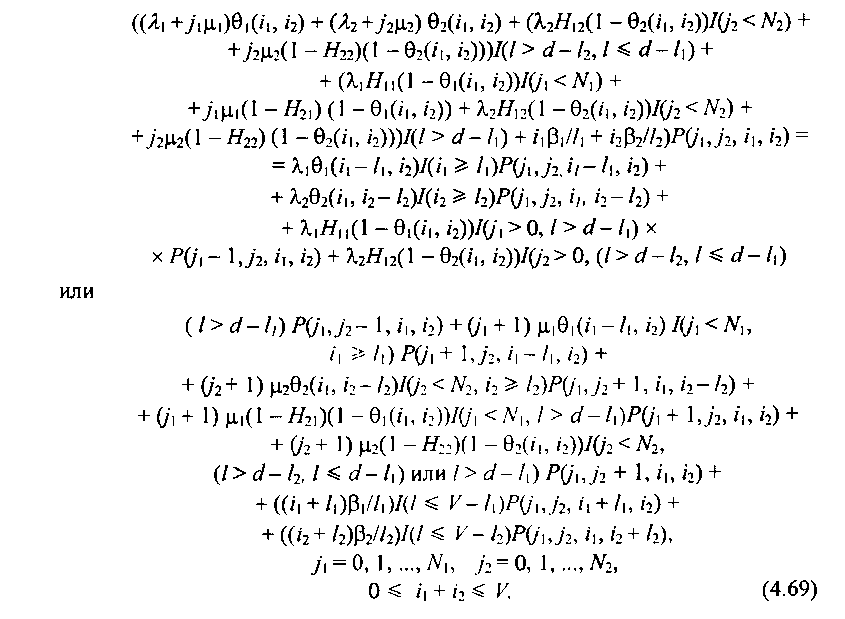
Здесь /(•) - индикаторная функция, задаваемая следующим образом: /(•) = 1, если условие, сформированное в скобках, выполняется, и /(•) = 0 - в противном случае. Систему уравнений (4.69) удобно решать итерационным методом Гаусса-Зейделя.

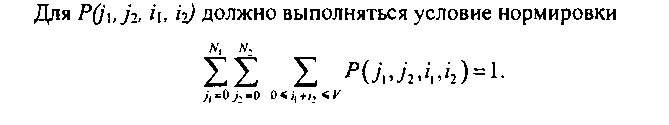
Основные вероятностные характеристики модели, входящие в записи законов сохранения (см. формулы (4.70)-(4.73)) и определяющие качество обслуживания вызовов и пропускную способность, имеют вид:

• вероятность потерь первичного вызова первого потока:

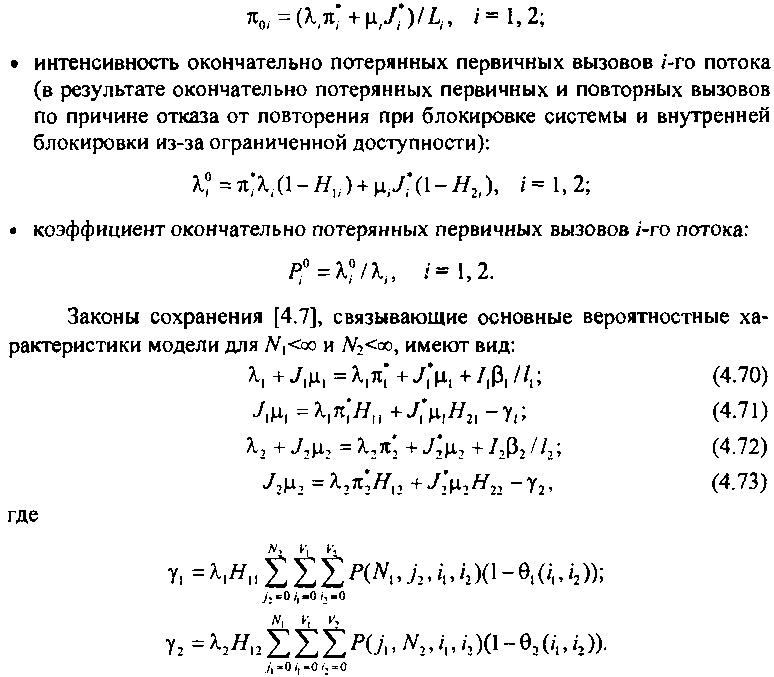
Законы сохранения имеют важное значение при исследовании систем с повторными вызовами. В частности, используя их при определении вероятностных характеристик, можно установить зависимости между отдельными вероятностными характеристиками модели.

⇐Среднее число попыток установления соединения в узлах коммутации | Мультисервисные телекоммуникационные сети | Результаты численных исследований системы с повторными вызовами⇒