Понятие эффективной доступности (ЭД) КС, введенное в [3.3, 3,5], является фундаментальным понятием, используемым в ряде современных методов расчета явных и условных потерь в структурно-сложных КС [3.4, 3.7-3.13]. Однако задача строгого определения ЭД до настоящего времени еще не решена. Известные приближенные методы определения ЭД [3.3, 3.4, 3.9-3.13] базируются на ограничениях, налагаемых на структуру КС в отношении связности, числа звеньев, законов межзвенных кроссировок, емкости, вида распределений числа одновременно занятых выходов отдельных коммутаторов системы и др. В результате область применения этих методов для расчета важнейших статистических характеристик КС таких, как вероятность потерь, вероятность ожидания начала обслуживания вызовов и т. п., оказывается ограниченной даже для режима одноканальной коммутации. Учитывая структурные особенности систем МК и особенности их работы, применение указанных методов проблематично. Поэтому представляется важным разработка такого метода определения ЭД, который позволил бы осуществлять расчет вероятностных характеристик систем МК ЦСИС.

Рассмотрим вопрос об эффективной доступности более подробно. Для этого сначала обратимся к однородной КС, работающей в режиме группового искания (ГИ) с одноканальной коммутацией и не имеющей концентрации соединительных путей. Будем считать, что на пучок каналов рассматриваемого направления искания поступает пуассоновская нагрузка. В процессе работы КС пребывает в состояниях каждое из которых ха рактеризуется числом и конфигурацией соединений, устанавливаемых в системе. Введем дополнительно числовую характеристику состояния - величину с/Д*?), г-1, А, которая представляет собой число выходов в направлении искания г, доступных некоторому фиксированному входу системы. Назовем эту величину мгновенной доступностью. Запишем выражение для вероятности потерь в направлении г, выразив ее через мгновенную доступность. Для этого разобьем множество допустимых состояний Я КС на У_г+1 непересекающихся подмножеств, причем в качестве признака разбиения выберем число установленных в направлении г соединений:

Общий вид коэффициента блокировки сгД-) зависит от структуры КС, величины и характера нагрузки, алгоритма выбора свободного соединительного пути. Для КС сложной структуры проблема строгого нахождения выражения для ст_г(-) в общем виде еще не решена. Поэтому в дальнейшем будем считать, что среди всех возможных состояний исходящего пучка с х занятыми каналами состояния, в которых имеется <} фиксированных каналов, встречаются равновероятно. При таком предположении, часто применяемом при расчете потерь в КС (смотри, например, [3.9]), приходим к так называемому эрланговскому коэффициенту блокировки

Предположение о равновероятности состояний с х занятыми каналами в пучке при d = const позволяет получить точное выражение вероятности потерь по крайней мере для класса однозвенных КС с идеальным неполнодоступным включением выходов.

Задачу определения вероятности потерь в КС можно сформулировать теперь несколько иначе, а именно: существует ли представление (3.3) в виде:

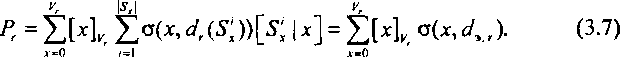
Параметр d_xвходящий в правую часть (3.7), будем в дальнейшем называть эффективной доступностью в направлении искания и понимать его в смысле выполнения равенства (3.7). Если для (3.7) принять допущение (3.6), то (3.7) переходит в известную формулу Эрланга для идеального неполнодоступного включения с той лишь разницей, что в формуле Эрланга параметр d является независимым, а в рассматриваемом случае d_%rявляется функцией структуры многозвенной КС, нагрузки и алгоритма выбора соединительного пути. Однако при фиксированных структуре КС, нагрузке и алгоритме выбора пути параметр d_xr= const. При этих условиях для рассматриваемой задачи можно применить теорему о вероятности потерь для идеального неполнодоступного включения [3.6], которая в нашем случае формулируется следующим образом:

где у,. - нагрузка, обслуженная одним выходом направления г.

Выражение (3.11) совпадает с выражением эффективной доступности, полученной в [3.13] при условии, что процесс занятия выходов в направлении искания можно описать с помощью априорно выбранного распределения вероятностей занятия выходов в полнодоступном пучке. В качестве такого распределения в [3.13] используется распределение Бернулли.

Эти предположения позволили в [3.13] получить формулу вероятности потерь в двух- и трехзвенных КС, работающих в режиме группового искания. Погрешность расчетов по этим формулам оказывается соизмеримой с погрешностью расчетов по соответствующим формулам Якобеуса [3.9] для случая биномиального распределения занятых выходов коммутаторов на всех звеньях КС. Таким образом, применимость формул [3.9] ограничивается областью малых значений вероятности потерь. Вместе с тем приведенные выше рассуждения показывают, что выражение (3.11) можно понимать и в более широком смысле, а именно как асимптотическую оценку эффективной доступности при V -> оо и предположении, что число занятых каналов в направлении искания подчиняется распределению общего типа - распределению (3.5), учитывающему структуру многозвенной КС.

Установление факта, что (3.11) имеет достаточно общий характер, дает основание полагать, что если бы были известны семиинварианты доступности с учетом их связи со структурой КС, характером нагрузки и алгоритмом выбора пути, то при использовании распределения (3.5) появилась бы возможность на базе единого методологического подхода разработать методы расчета вероятностных характеристик КС для случаев, когда известные методы либо приводят к недопустимой погрешности, либо неприменимы вообще, что имеет место для внедряемых в настоящее время электронных телефонных систем и систем МК. Поэтому дальнейшей задачей этой главы является определение симиинвариантов доступности.

Раскроем (3.11). Известно, что со₍- семиинвариант 1-го порядка есть рациональная функция первых 1-х начальных моментов, а первый и второй семиинварианты соответственно равны математическому ожиданию и дисперсии рассматриваемой случайной величины. Обозначим мгновенную доступность, рассматриваемую как дискретную случайную величину, б, ее математическое ожидание - М(8) = <1_Г, дисперсию - М(8-с1_г)², начальные моменты 1-го порядка - М(8'). Запишем в принятых обозначениях выражение для эффективной доступности, ограничившись первыми тремя членами разложения (3.11):

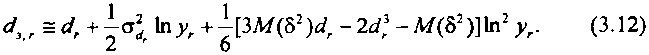
Из (3.11) и (3.12) можно установить важное свойство ЭД: при достаточно высоком использовании каналов исходящего направления ЭД можно аппооксимигювать математическим ожиданием доступности, так как

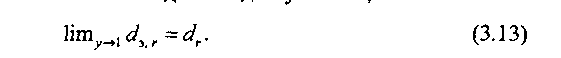
Однако в области малых и средних значений величины использования каналов в пучке вопрос о числе членов разложения (3.11), достаточных для аппроксимации ЭД, требует дополнительного исследования.

Таким образом, задача определения эффективной доступности сводится к определению:

• моментов доступности КС,

• необходимого числа членов разложения (3.11), достаточного для обеспечения необходимой точности при решении инженерных задач.

⇐Вероятность блокировки выходов пространственно-временных коммутационных систем | Мультисервисные телекоммуникационные сети | Средняя доступность многозвенных кс⇒