Выбор той или иной многокаскадной КС можно осуществить на основе сравнения их важнейших характеристик. На рис. 10.20 показана зависимость относительной ширины полосы пропускания от числа каскадов небуферированной Дельта-системы, содержащей КЭ емкостью 2x2. Как ясно из графика, пропускная способность системы быстро убывает с ростом числа каскадов.

Из анализа графика можно сделать вывод о малой эффективности небуферированной системы. Это объясняется тем обстоятельством, что в небуферированных КС велика вероятность блокировки. Вероятность блокировки резко возрастает с увеличением числа каскадов системы, что сказывается на уменьшении величины полосы пропускания. Более важной характеристикой является пропускная способность. Очевидно, что пропускная способность повышается, когда возрастает размер буферов КЭ. Затраты на аппаратную реализацию представляют собой компромисс между задержкой, возникающей при коммутации и размером буфера, который должен иметь конечную емкость.

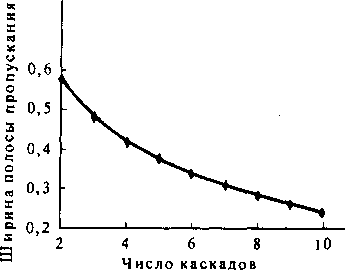
Рис. 10.20. Зависимость ширины полосы пропускания от числа каскадов небуферированной Дельта-системы с КЭ емкостью 2x2

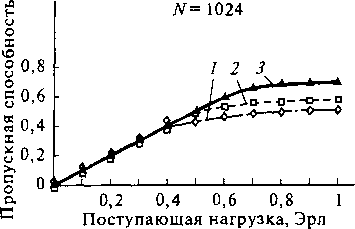
Рис. 10.21. Зависимость пропускной способности от поступающей нагрузки Дельта-системы:

1-п = 2,В=\;2 - п = 2,В = 2-,3 - п = 2, 5 = 4

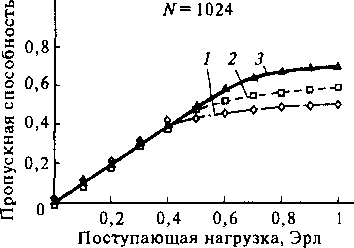
Рис. 10.22. Зависимость пропускной способности от поступающей нагрузки Дельта-системы:

/ - w = 4, Я = 1; 2 - п = 4, В = 2\3 - и = 4, 5 = 4

На рис. 10.21, 10.22, 10.23 приведены зависимости пропускной способности от поступающей нагрузки. Очевидно, что чем меньше емкость коммутаторов, тем больше буферов оказывается в системе, и, следовательно, тем выше ее пропускная способность. Наименьшая пропускная способность будет при одиночном буферном накопителе.

Наилучшие характеристики можно получить путем гибридного режима коммутации, а именно режима коммутации пакетов и режима коммутации каналов. Согласно этому методу, если ячейка встречает занятые звенья на промежуточных КЭ, то поведение КС соответствует режиму коммутации пакетов. С другой стороны, если все промежуточные звенья являются свободными, то КС ведет себя подобно небуферированной системе. Фактически это и есть режим быстрой коммутации пакетов (БКП).

На рис. 10.24 представлена зависимость пропускной способности буферированной Дельта-системы, работающей в режиме БКП. Ее пропускная способность примерно на 20 % выше, чем при классическом режиме пакетной коммутации.

На рис. 10.25 показана зависимость средней задержки от изменения пропускной способности при различных емкостях системы.

Значительное улучшение характеристик КС имеет место в модифици-

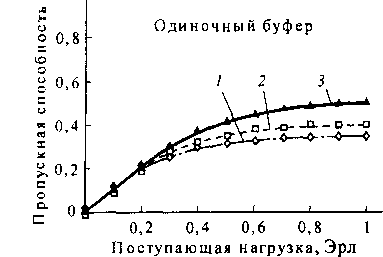
Рис. 10.23. Пропускная способность Дельта-системы с одиночным буфером:

1 - N = 256 х 256; 2 - N = 64 х 64; 3 - N = 16х 16

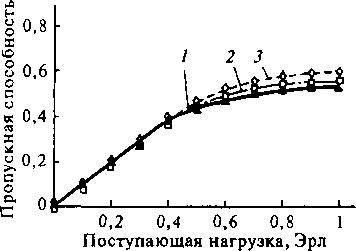
Рис. 10.24. Зависимость пропускной способности буферированной Дельтасистемы, работающей в режиме БКП:

/ - /V = 16 X 16; 2 - /У= 64 X 64; 3 - N = = 256 x 256

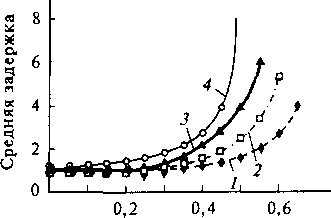
Пропускная способность, Эрл Рис. 10.25. Зависимость средней задержки от пропускной способности при различных емкостях системы;

/_ м= 4x4; 2 - N = 8x8; 3 - N = = 16 х 16; 4 - N = 64 х 64

рованной Дельта-системе. На рис. 10.26 показана зависимость нормированной ширины полосы от числа каскадов в КС различного типа. Наивысшую пропускную способность имеет небуферированная система (типа кроссбар), а улучшенные расширенные и скопированные системы существенно оказываются лучше, чем обычная Дельта-система.

На рис. 10.27 представлена зависимость пропускной способности от поступающей нагрузки в параллельной Дельта-системе. Графики зависимостей представлены для трех емкостей системы = 16, 64, 256. Как видно, пропускная способность до определенной нагрузки (а = 0,7 Эрл) практически не зависит от емкостей системы. И лишь при очень больших загрузках (а = 0,7 Эрл) зависимость от емкости системы оказывается существенной.

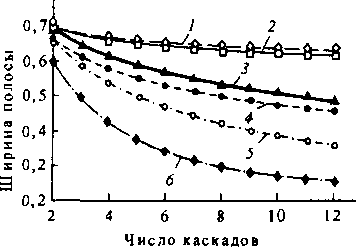
Рис. 10.26. Зависимость нормированной ширины полосы от числа каскадов:

1 - Кроссбар; 2, 3 - расширенная; 4, 5 - скопированная; 6 - Дельта

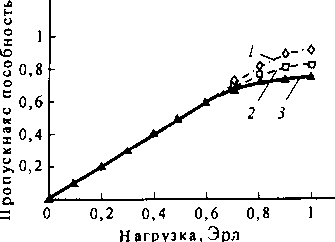
Рис. 10.27. Зависимость пропускной способности от поступающей нагрузки в параллельной Дельта-системе:

1 - Ы= 256 х 256; 2 - N = 64 х 64; 3 - Дг= 16 х 16

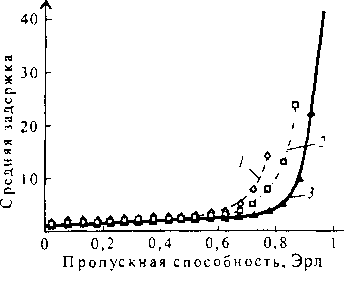
Рис. 10.28. Зависимость средней задержки от величины пропускной способности для параллельной Дельтасистемы:

1 -N = 16 х 16; 2 - И= 64 х 64; 3 - Ы = = 256 х 256

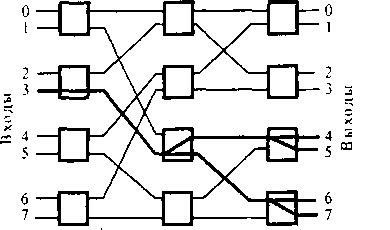
Рис. 10.29. Пример многоточечного соединения в Дельта-системе На рис. 10.28 изображены графики зависимостей средней задержки от изменения пропускной способности для параллельной Дельта-системы и тех же емкостей, как и для рис. 10.27. Анализируя эти графики, можно отметить, что средняя задержка ячеек в системе также становится существенно заметной при нагрузке а > 0,7 Эрл.

Рассмотренные КС можно использовать как для широковещательной связи, так и для случая многоточечных соединений. Рис. 10.29 иллюстрирует пример многоточечного соединения в Дельта-системе емкостью Л^= 8.

Литература 10.1. Adams J.L. The performance of LAN protocols // 18th International Seminar on the Teaching of Computing Science at University Level. University of Newcastle Upon Tyne, September 1985.

10.2. Adams J.L. The Orwell torus communication switch // CEPT Conference on Broadband Switching, Albufeira Portugal, January 1987.

10.3. Batcher K.E. Sorting networks and their applications // Proc. of AFIPS conf. 1968. P. 307-314.

10.4. Benes V.E. Mathematical theory of connecting networks and telephone traffic. Academic Press, New York, 1965.

10.5. Benes V.E. Optimal rearrangeable multistage connecting networks // Bell System Technical Journal, July 1964. P. 1641-1656.

10.6. Bernabei F„ ForcinaA., Listanti M. On non-blocking properties of Parallel Delta networks // Proc. of INFOCOM, 1988. New Orleans, USA, March 1988. P. 4A.2.

10.7. BernabeiF., List ant i M. Generalized Parallel Delta networks: a new class of rearrangeable interconnection networks. Submitted for publication.

10.8. BernabeiF., ListantiM. A hybrid switching exchange for broadband communications // Proc. of ICCC88, Tel Aviv, Israel, October 1988. P. A 2-2.

10.9. CCITT Red book. Recommendation X. 200.

10.10. ClosC. A study of non-blocking switching network // Bell System Technical Journal, Vol. 32, March, 1953. P. 406-424.

10.11. COST 202 bis - Final report of expert group on ATM switch structures // European cooperation in the field of scientific and technical research. Brussels, 1988. P. 68.

10.12. Coudreuse, Servel. PRELUDE: An asynchronous time-division switched network //Globecom, 1987.

10.13. Day C., Giacopelli J„ Hickey J. Applications of self routing switches to LATA fiber optic networks // ISS87, Phoenix, March 1987. P. A7.3.

10.14. Dias D.M.. Kumar M. Packet switching in NlogN multistage networks // GLOBECOM, 84, Atlanta, December 1984. P. 5.2.

10.15. Krustal C.P., Smir M. The performance of multistage interconnection networks for multiprocessors// IEEE Trans, on Computers, December 1983. P. 1091--1099.

10.16. Prycker M. De and Somer M. De. An ATM broadband switching exchange with distributed control // GSLB - Seminar on Broadband Switching. P. 266-275, Groupe Special des Communications a Large Bande (GSLB) CEPT, Femmel-detechnisches Zentralamt der Deutschen Bundespost, D-6100 Darmstadt. GSLB seminar, January 19 and 20, 1987. Albufeira. Portugal.

10.17. Somer M. De. Building a mathematical model describing the behaviour of a variable bitrate switching network // ITC Seminar. Brussels, May 5 to 7, 1986.

Прежде чем решать задачу, подумай, что делать с ее решением Р. В. Хемминг

⇐Коммутационная система с одним промежуточным путем между парой вход-выход | Мультисервисные телекоммуникационные сети | Метод расчета вероятности потерь ячеек в системе бкп⇒