Для современных программно-управляемых систем связи можно привести много примеров применения дисциплины обслуживания с ограниченным ожиданием. Это обслуживание приоритетных абонентов, работа пучков групповых приборов, обработка статистической информации в коллекторах данных и т. д. Кроме того, во всех управляющих системах как с центральным, так и с распределенным управлением организуются буферы фаз состояний оборудования и сообщений от других программ и устройств, которые с заданным тактом сканирования разгружаются программами-диспетчерами.
В подобных системах можно определить два вида ограничений: предельно допустимая длина очереди и максимальное время ожидания начала обслуживания.
Рассмотрим задачу определения вероятности потерь в полноступной системе массового обслуживания (СМО) с ограниченной очередью и ограниченным временем пребывания в очереди, следуя [7.4]. Время ограничения пребывания в очереди является константой, определяемой особенностями функционирования узла коммутации. Исследование систем с ограниченным ожиданием представляет значительную сложность, так как случайный процесс v(t) (число требований в системе) в общем случае не является марковским процессом. Известны результаты, полученные для систем с ограниченным числом мест ожидания и ограниченным временем ожидания [7.2,7.8].
В [7.3] была сделана попытка расчета системы с ожиданием с обоими видами ограничений, однако выведенная автором формула неверна. Не обсуждая вывод формулы в [7.3], проиллюстрируем некорректность результата. Так в области больших нагрузок А при малом числе мест ожидания и отсутствии ограничения на время ожидания в очереди вероятность потерь Р, рассчитанная по формуле из [7.3], превосходит величину потерь в V-канальной системе с явными потерями Еу(А). При одном месте ожидания, например, имеет место выражение:

При этом в интервале времени О требования, занимающие в очереди 2-, 3-, 4-, к-е место не оказывают влияния на процесс обслуживания, что позволило провести фазовое укрупнение процесса г('г') и перейти к процессу (К0> £■(*))> ЧТО, в свою очередь, позволило решить систему уравнений Колмогорова в явном виде [7.6]. Для полнодоступного пучка с входным потоком, зависящим от состояния системы, конечной очередью и ограниченным временем ожидания выводится формула для вероятности потерь по вызовам и исследуется поведение функции потерь при различных значениях параметров.
Определим постановку задачи. В К-канальную СМО поступает поток однородных требований. Вероятность поступления нового требования в интервале (/, г + А) равна ХкА + 0(А -» 0), если в системе в момент / находится к требований.
Длительность обслуживания на 1-м канале - экспоненциально распределенная случайная величина со средним ц'1(1 =1, •••> V). Емкость буфера ожидающих заявок Ь > 0, время ожидания в очереди ограничено константой а. Выбор начала обслуживания из числа свободных заявок - равновероятный, порядок обслуживания очереди - прямой («первым пришел - первым обслужился»). Для этого случая получено стационарное распределение процесса \{1) - числа заявок в системе [7.6]:
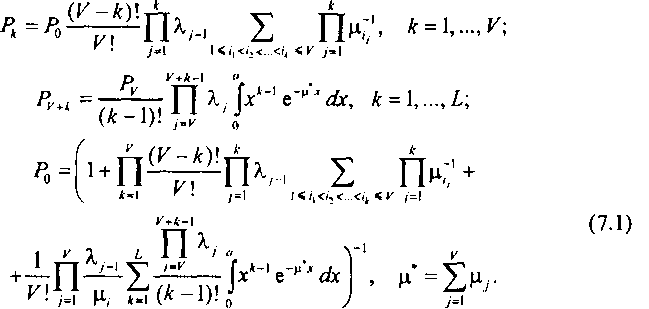
Вызов, поступивший в подобную систему, получит отказ в обслуживании в случае занятости всех мест ожидания. Кроме того, ожидающий вызов, не обслуженный в течение времени а, также будет потерян. Вероятность потерь по вызовам будет равна сумме вероятности Р\ - занятости V линий и Ь мест ожидания и вероятности Рц того, что за время а вызов не обслужен (события несовместны):
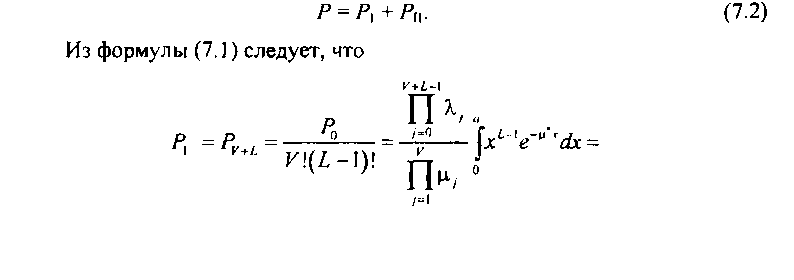

ле полной вероятности:
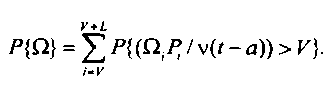
Здесь □, - событие, определяющее поступление вызова в интервале (г - а -А, / - а) при состоянии системы у(1- а- И) =
Таким образом:
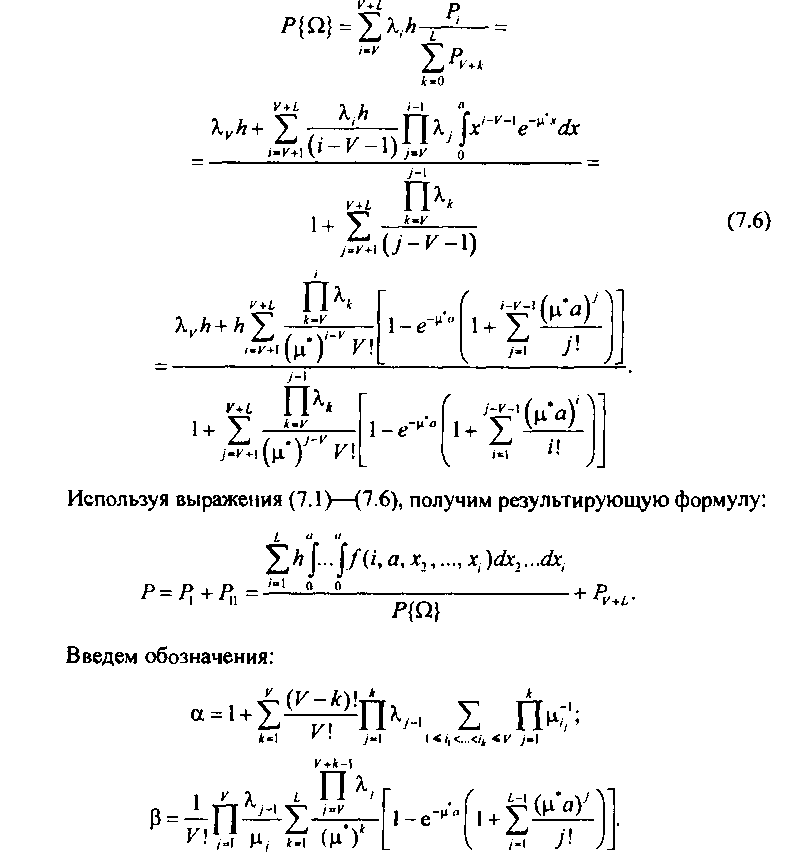
Тогда выражение полной вероятности Р можно представить в следующем виде:

На рис. 7.1-7.4 приведены графики потерь при различных значениях параметров. На рис. 7.1 приведена зависимость вероятности потерь от интенсивности поступающей нагрузки при фиксированной емкости буфера Я: Хк= X, ц* = ц, У = 10.
На рис. 7.2 показана зависимость вероятности потерь от интенсивности поступающей нагрузки при фиксированных значениях ац и параметрах: Хк= X, ц* = ц, У = 10.
На рис. 7.3 изображена зависимость вероятности потерь от числа мест ожидания Я: Хк= X, ц* = ц, А/У = 0,9, У = 10.
На рис. 7.4 представлена зависимость вероятности потерь от величины ограничения по времени ац: Хк- X, ц* = ц, А/У = 0,9, У = 10.
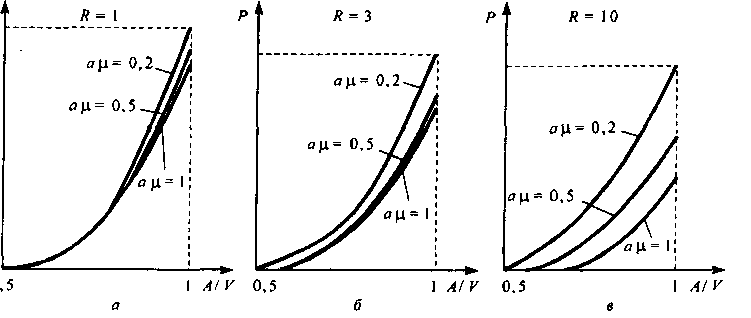
Рис. 7.1. Зависимость вероятности потерь от интенсивности поступающей нагрузки при фиксированной емкости буфера Я: X* = X, ц* = ц, V- 10
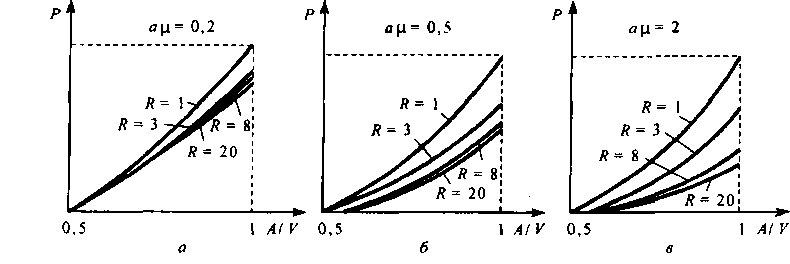
Рис. 7.2. Зависимость вероятности потерь от интенсивности поступающей нагруз ки при фиксированных значениях ац: X* = X, ц* = ц, У= 10
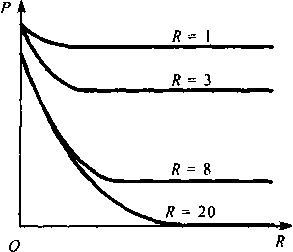
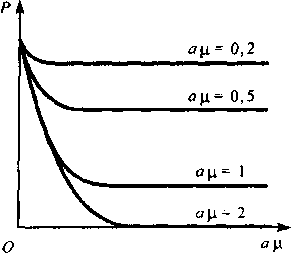
Рис. 7.3. Зависимость вероятности по- Рис. 7.4. Зависимость вероятности потерь терь от числа мест ожидания Я: Хк= X, от величины ограничения по времени ац: ц* = ц, Л/У= 0,9, У= 10 Хк= х, щ = ц, Л/У= 0,9, У= 10
Из представленных графиков видно, что существует тесная взаимосвязь между обоими видами ограничений. Так фиксация одного ограничения определяет диапазон изменения функции потерь при изменении другого ограничения. Действительно, при фиксации, например, емкости буфера /? график потерь изменяется в диапазоне от вероятности потерь для системы с явными потерями до вероятности потерь в системе с ограниченным числом мест ожидания. Аналогичная зависимость наблюдается при фиксации ца.
Результаты этого раздела можно применять не только при анализе работы УУ узла ЦСИС, но и при расчете оборудования цифровых телефонных станций, обслуживающих потоки вызовов от приоритетных абонентов, расчете пучков групповых приборов на междугородных станциях, организации обработки управляющими устройствами различных интерфейсных буферов и коллекторов данных статистики, в ряде других задач. Кроме того, полученные результаты можно использовать для приближенной оценки потерь в коммутационных схемах, работающих с ограниченным ожиданием.
⇐Параметры избыточной и обслуженной нагрузок в направлениях связи системы многоканальной коммутации | Мультисервисные телекоммуникационные сети | Идеально симметричная неполнодоступная система обслуживающих приборов с ограниченным временем ожидания и конечной очередью⇒
