Общие замечания В настоящее время проводятся интенсивные исследования в области теории построения Ш-ЦСИС. Среди комплекса проблем, которые предстоит решить в этой области, основной является проблема оптимального построения УК. Предполагается, как это было показано выше, что в Ш-ЦСИС сообщения, поступающие от разнородных источников, имеют униформное представление. В качестве стандартного сообщения в Ш-ЦСИС, в соответствии с рекомендацией МККТТ, принят пакет, имеющий информационное и адресное поле 48 и 5 октетов соответственно, получивший название ячейки (cell).

Для передачи информации используют принцип асинхронно-временного мультиплексирования. В соответствии с этим принципом ячейка передается как самостоятельная информационная единица, занимая любой свободный и доступный интервал времени в кадре. Такой способ мультиплексирования обусловливает статистическое заполнение кадра. Эту операцию выполняет статистический мультиплексор (см. гл. 9).

Поступающие по статистически уплотненным входящим линиям информационные ячейки на узле коммутации должны быть перераспределены по аналогичным исходящим линиям. Эта операция осуществляется в режиме БКП. Коммутация ячеек на узле БКП может быть выполнена с применением различных средств коммутации: многозвенных КС, общей шины или памяти, коммутационных торов (см. разд. 10.1).

Однако в зависимости от выбранных средств коммутации в системе БКП возникают ситуации, когда ячейка не может быть немедленно передана в исходящую линию из-за передачи в данный момент по этой линии другой ячейки. Эта ситуация называется конфликтом (collision). В случае конфликта ячейка ожидает подходящего момента передачи в буфере, рассчитанном ю*

на хранение Ь ячеек. Если буфер переполняется, то возможна потеря ячеек. Таким образом, обслуживание ячеек на узле БКП осуществляется по системе СМО с потерями и ожиданием.

Рассмотрим задачу оценки вероятности потерь ячеек, следуя [11.2].

11.1.1. Структура системы БКП

На рис. 11.1, а показан в условном представлении базовый коммутационный элемент (БКЭ). БКЭ имеет п входов и т выходов. Каждый вход БКЭ оборудован буфером с местами для ожидания, причем емкость каждого буфера равна Ь. Выходы буферов являются входами в КС БКП. Как было отмечено выше, для построения КС используют различные принципы. Однако важным требованием, предъявляемым к КС, является минимизация конфликтов внутри них. Предполагается, что конфликты ячеек возникают при попытке их передачи по выбранной исходящей линии.

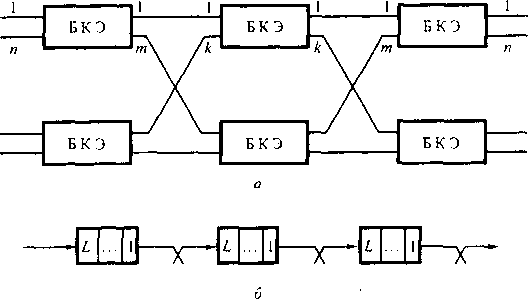
БКЭ используют для построения многокаскадной системы БКП. Структура системы БКП может быть различной. На рис. 11.2 приведена трехкаскадная система БКП. В этой системе ячейке, поступившей по некоторой входящей линии, для передачи в требуемую исходящую линию может быть представлено до т путей. Любой из возможных путей, использованный для передачи ячейки в системе (рис. 11.2, а), будет содержать три последовательно включенных буфера (рис. 11.2, б). В общем случае, если система БКП имеет 5 каскадов, виртуальный канал передачи будет содержать 5 буферов с Ь местами ожидания.

11.1.2. Вероятность потерь ячеек в БКП

Потери ячеек в рассматриваемой модели БКП (см. рис. 11.2) возникают при переполнении любого буферного накопления. Так как потери ячеек возможны, когда буфер подключается через КС к одной из исходящих из БКЭ линии, то оценка вероятности потерь в БКЭ сводится к расчету вероят-

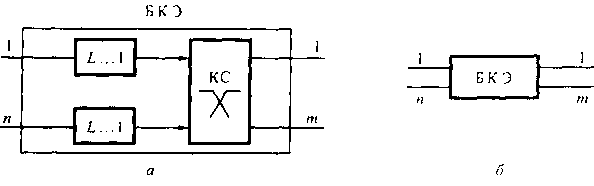
Рис. 11.1. Условное обозначение БКЭ: а - структура; 6 - условные обозначения

--14 1'1-у-Н-М--)г*

в Рис. 11.2. Структурная схема трехкаскадной системы БКП: а - трехкаскадная КС, построенная на БКЭ; 6 - схема передачи ячейки от входа к выходу ности потерь в однолинейной СМО с буфером конечной емкости. В такой СМО обслуживание осуществляется детерминированно (D), так как все ячейки имеют одинаковую длину. Закон поступления ячеек в СМО, как показывают исследования, следует считать произвольным с независимым разделением интервалов между моментами поступления ячеек (GI). Таким образом, используя обозначения Кендалла, задача расчета вероятности потерь ячеек сводится к задаче расчета потерь заявок в СМО вида: GI/D/1/L. Строгое решение этой задачи отсутствует. Для получения приближенной оценки вероятности потерь будем считать, что поступающая нагрузка будет задаваться своими первыми двумя моментами распределения - интенсивностью нагрузки R и ее дисперсией ст". В дальнейшем будем использовать не саму дисперсию ст², а отношение Z = ст²//?, где Z - коэффициент дисперсии. Таким образом, поступающая нагрузка будет задаваться парой (/?, Z).

Одним из подходов для приближенного определения вероятности потерь ячеек является подход, основанный на аппроксимации системы GI/D/ML в определенном смысле «близкими системами», для которых либо разработаны строгие методы расчета, либо имеются оценки интересующей характеристики. В качестве такой системы может быть выбрана однолинейная система с пуассоновской поступающей нагрузкой и L* числом мест ожидания: M/DIML*.

Рассмотрим систему M/D/ML* при той же интенсивности нагрузки R, что и в системе GI/D/ML. Вероятность потерь в системе MJD/ML можно определить согласно [11.6] по формуле

где тсо - стационарная вероятность застать систему пустой. Согласно [11.6], она равна

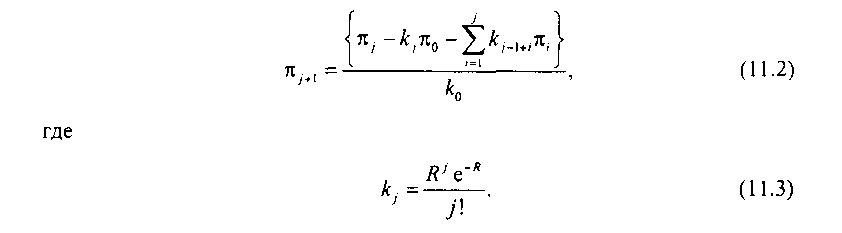
Рассмотрим пуассоновскую однолинейную систему МЫШЬ*. Подберем в ней такое число мест ожидания Ь*, при котором система Ы/Ы/1/Ь* при интенсивности нагрузки Л будет иметь такую же вероятность потерь, как и система М/ИШЬ. Как известно (см., например [11.6]), вероятность потерь в системе Ы/Ы/1/Ь*

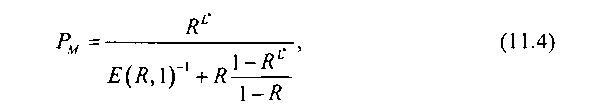
где E(R, 1) - вероятность потерь, определяемая по первой формуле Эрланга при емкости пучка каналов V= 1 и нагрузке R.

Эквивалентное число ожидания L* в системе Ы/ЫШЬ* можно вычислить по (11.4), если принять, что Р_м= Р₀. Таким образом, используя (11.1) и (11.4), можно перейти к системе Ы/ЫШЬ*, которая при одной и той же интенсивности будет иметь такие же потери, как и система Ы/D/l/L.

Систему Ы/ЫШЬ* можно, в свою очередь, использовать для приближенной оценки вероятности потерь в системе GI/M/ML*, если поступающая нагрузка будет задана парой (R, Z). Для этого может быть использована Z-аппроксимация Витта [11.13], согласно которой вероятностное поведение N-линейной системы GI/M/N/L* в области больших нагрузок может быть приближенно описано пуассоновской системой, на которую поступает нагрузка Л_экв= Л/со², с числом обслуживающих приборов У_экв= V/ю²и числом мест ожидания „ = Ысо, причем:

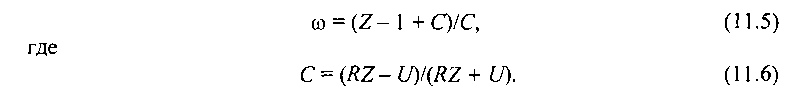
Параметр {/, входящий в (11.6), можно определить методом линейной регрессии на основе данных имитационного моделирования. Исследования

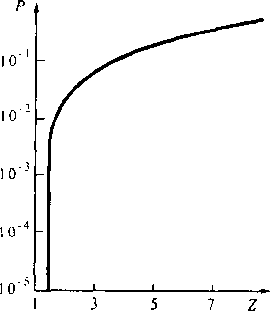
Рис. 11.3. Зависимость вероятности потерь ячеек от коэффициента дисперсии поступающей нагрузки

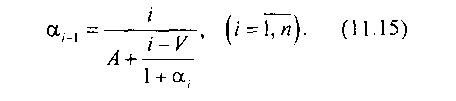
Формула (11.14) применима, если 0,95Л.

Вычисления (11.14) начинают с выбора а„ = 0. Важным вопросом является определение порядка непрерывной дроби и, так как от величины п зависит число точно определяемых знаков в (11.10). Особенно важно обеспечить необходимую погрешность при Z > 1, так как в этом случае К*_экв< 1 и представление формулы Эрланга в виде (11.13) имеет сравнительно медленную сходимость.

Вероятность потерь, определяемую из (11.10), можно использовать для приближенной оценки вероятности потерь в системе GI/D/1/L, в которой поступающая нагрузка задается парой (R, Z).

На рис. 11.3 представлена зависимость вероятности потерь ячеек от коэффициента дисперсии поступающей нагрузки при фиксированных значениях R. Моделирование осуществлялось при R = 0,5 Эрл и L = 40.

Анализ зависимости вероятности потерь ячеек Р от изменения коэффициента дисперсии Z позволяет сделать вывод о том, что эта вероятность для системы БКП существенно зависит от коэффициента дисперсии поступающей нагрузки. Особенно сильно проявляется этот эффект в области малых потерь. Даже сравнительно небольшое увеличение коэффициента дисперсии Z приводит к резкому возрастанию потерь в системе (см. рис. 11.3).

Неучет второго момента нагрузки при проектировании узлов БКП может привести к резкому ухудшению качества обслуживания в условиях, когда поступающая нагрузка даже незначительно отличается от пуассоновской.

11.2. Анализ работы статистического мультиплексора 11.2.1. Статистический мультиплексор как система массового обслуживания В гл. 9 в общих чертах рассматривался принцип работы СМ, используемого для формирования объединенного исходящего цифрового потока.

Как уже отмечалось СМ - управляемый буферный накопитель, на который поступают ячейки от генераторов ячеек. Применение статистического мультиплексирования возможно только при переходе к асинхронному способу передачи (АСП) информации, так как АСП позволяет учесть статистические особенности цифровых потоков, создаваемых отдельными классами пользователей и осуществить статистическое уплотнение исходящего канала (тракта передачи).

Рассмотрим работу СМ как СМО. При проектировании СМ решают следующие проблемы:

• классификация пользователя в отношении скорости мультиплексирования;

• распределение пропускной способности исходящего тракта с целью обеспечения совокупности разнородных пользователей требуемого качества обслуживания (вероятности потерь информационных ячеек и время их задержки в СМ);

• управление трафиком для обеспечения того, чтобы возможные изменения в поведении определенного класса пользователей не оказывали влияние на потери информационных ячеек, допустимые для других классов пользователей.

Оценки вероятностей потерь ячеек и времени ожидания в буферном накопителе при статистическом мультиплексировании с учетом указанных выше факторов получены в ряде работ и, в частности, в [11.7-11.9].

Одним из основных преимуществ систем связи, использующих АТМ, является возможность наилучшим образом использовать ресурсы систем передачи за счет статистического мультиплексирования информационных потоков, поступающих от большого числа пользователей (источников ячеек). Организация доступа пользователей к общему оптоволоконному каналу связи через мультиплексор приводит к необходимости решения при этом трех задач:

1) построение классификации пользователей по структуре создаваемой ими нагрузки;

2) оценка скорости передачи, предоставляемой заданной группе пользователей различных классов, необходимой для того, чтобы гарантировать нормируемое качество обслуживания, которое выражается в терминах вероятности потерь ячеек и их задержки;

3) создание процедуры управления нагрузкой пользователей.

Целью математического моделирования, таким образом, является решение задачи 2, однако при построении модели системы АТМ необходимо отразить в ней как принадлежность абонентов тем или иным классам (задача 1), так и наличие или отсутствие, если это будет признано целесообразным, процедуры управления нагрузкой (задача 3).

Необходимо отметить две возможные постановки задачи управления нагрузкой:

• наблюдение за нагрузкой отдельного пользователя и проверка соответствия ее заявленному классу, а также сглаживание этой нагрузки так, чтобы изменение ее параметров не оказывало чрезмерного влияния на потери ячеек других пользователей (индивидуальное управление);

• управление соединениями, т. е. процедура принятия решения о том, может ли быть установлено еще одно соединение и не приведет ли это к увеличению потерь и/или задержек ячеек сверх нормируемых (интегральное управление).

Одним из примеров индивидуального управления является управление методом «протекающего ведра», описанный в гл. 9. При этом управлении поток ячеек изменяется так, как если бы он проходил через однолинейную СМО с детерминированной длительностью обслуживания, конечным накопителем и дисциплиной обслуживания FIFO. Необходимо отметить, что решение вопроса о том, какими выбрать величины длительности обслуживания и емкости накопителя этой фиктивной СМО, а также, как при этом меняются параметры трафика и, в частности, какие возникают потери, является само по себе сложной задачей, решение которой известно лишь при самых простых предположениях относительно исходного трафика.

Очевидно, что если выбрать скорость обслуживания в фиктивной СМО равной или незначительно превосходящей среднюю скорость поступления ячеек, а накопитель достаточно большой емкости, то результирующий поток ячеек, т. е. выходящий из СМО, будет полностью сглаженным. Однако задержки ячеек в СМО могут быть очень значительными.

С другой стороны, скорость обслуживания в фиктивной СМО может соответствовать максимальной скорости поступления ячеек. В этом случае поток ячеек совсем не сглаживается, а задержки минимальны. Ясно, что в первом случае статистическое мультиплексирование нескольких потоков, подвергшихся процедуре управления методом «протекающего ведра», сводится к модели многоканальной коммутации, так как каждому источнику на все время соединения должна быть предоставлена фиксированная скорость передачи или, другими словами, фиксированная доля временных каналов - слотов. В другом случае статистическое мультиплексирование может дать существенное преимущество за счет одновременного обслуживания большего числа источников, однако это увеличивает долю потерянных ячеек.

Таким образом, оптимальные параметры индивидуального управления потоком методом «протекающего ведра» принимают промежуточные между двумя рассмотренными случаями значения, причем они зависят от того, какое число соединений и от каких источников установлено.

Упрощенно воздействие процедуры «протекающее ведро» на пульсирующий (берстный) поток ячеек можно описать следующим образом. (Пульсирующим в данном разделе назван поток, создаваемый источником, который поочередно находится в двух состояниях. В одном из состояний - активном - источник генерирует поток ячеек постоянной интенсивности, в другом - состоянии паузы - источник не посылает ячеек.)

Пусть А - средняя длительность активного периода источника, А, - интенсивность генерирования ячеек в активном состоянии, 5 - средняя длительность паузы между периодами активности, £> - длительность детерминированного обслуживания в фиктивной СМО. Тогда берстность, т. е. отношение максимальной интенсивности поступления ячеек к средней, имеет вид

Ясно, что при емкости накопителя этой фиктивной СМО, достаточной для того, чтобы потери не превышали значения 10~⁹… 10“'°, среднюю интенсивность потока ячеек, покидающих СМО, можно принять равной интенсивности их поступления, т. е. равной XA(S + А). С другой стороны, в периоды занятости ячейки покидают систему с интенсивностью HD. Обозначив соответствующие характеристики потока ячеек, выходящего из СМО, через A_lb, Slb, ^lb> Blb и приняв дополнительно, что в периоды активности источник генерирует ячейки через детерминированное время, получим

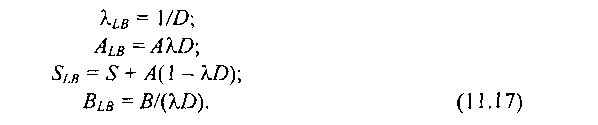
Отсюда видно, что пульсирующий поток сглаживается, если D > 1/Х, т. е. скорость обслуживания в фиктивной СМО меньше скорости генерации ячеек в активном состоянии пользователя.

Среднее время ожидания в фиктивной СМО (задержка ячеек в результате применения процедуры «протекающее ведро»):

Сглаживание потока с помощью процедуры управления МПВ происходит, главным образом, за счет задержек ячеек. Известной процедурой управления потоком является также процедура «скользящее окно» (Sliding Window) [11.12], при которой происходит сброс ячеек в том случае, если их суммарное число за промежуток времени определенной длины превысит заданную величину. Эта процедура управления сглаживает трафик за счет увеличения потерь ячеек тех источников, нагрузка от которых не соответствует параметрам, согласованным в момент установления соединения.

Более сложные процедуры управления индивидуальной нагрузкой и оценка их эффективности предложены в [11.5].

11.2.2. Анализ задержки и потерь ячеек в очереди статистического мультиплексора В системах АТМ одним из основных элементов, требующих анализа, является очередь ячеек, которая образуется перед передающим устройством в результате его использования многими источниками. Такие очереди могут образоваться как на выходе из узла сети АТМ, так и внутри КС. Основная сложность при анализе этих очередей состоит в том, что размерность задачи становится очень большой, если мы принимаем достаточно реалистичные предположения относительно характера поступающего трафика [11.1, 11.8]. Упрощение описания трафика приводит к большим ошибкам в определении интересующих нас характеристик: среднего времени ожидания и вероятности потерь ячеек. Разные виды источников могут быть чувствительны к увеличению задержек сверх определенного значения и/или увеличению доли потерянных ячеек. Необходимо отметить, что, как показано в [11.10], для определения различных характеристик могут быть приняты разные упрощающие допущения относительно характера поступающего потока ячеек. Например, средняя задержка ячеек очень слабо зависит от корреляционных свойств потока и его периодичности. Это значит, что для расчета средней длительности ожидания можно принять, что поступающий поток описывается групповым потоком Бернулли.

Обозначим через Л(г) производящую функцию (ПФ) числа ячеек, поступающих за такт (время выдачи в канал одной ячейки). ПФ следует выбрать так, чтобы совпадали хотя бы первые моменты суммарного числа ячеек, генерируемых всеми источниками за период времени, характерный для периодических изменений в .интенсивности трафика, т. е., например, за усредненный интервал времени между началами двух периодов активности. Другой способ выбора длины указанного временного интервала состоит в определении такой величины (, при которой отношение дисперсии к среднему значению процесса Щх) достигает в точке / своего максимума.

Достаточно точную оценку сверху средней длительности ожидания IV можно получить, если принять, что накопитель для ячеек имеет неограниченную емкость. Тогда

В [11.10] показано, что на значение л сильно влияют корреляционные свойства поступающего потока. В [11.11] предложен подход для оценки блокировки по времени накопителя с учетом коррелированности потока, однако неясно, как связать блокировки по времени с вероятностью потерь л. В частности, в этой работе показано, что блокировки по времени оцениваются сверху вероятностью того, что за интервал длительности R поступит не менее R ячеек. Сопоставляя результат [11.11] с предлагаемым здесь методом расчета л, можно сделать вывод, что наилучшим образом оценить влияние коррелированности потока на значение л можно, выбрав при определении A(z) интервал длительности L в качестве характеристического.

⇐Сравнительный анализ вероятностных характеристик систем быстрой коммутации пакетов | Мультисервисные телекоммуникационные сети | Метод расчета пропускной способности звена передачи ш-цсис с atm-технологией при мультисервисном обслуживании⇒