Одной из важнейших вероятностных характеристик КС является среднее число попыток установления соединения (ПУС). Знание этой характеристики позволяет оценить загрузку УУ, оптимизировать его работу. В настоящее время отсутствуют в достаточной мере теоретически обоснованные методы оценки этой характеристики, что не позволяет оптимизировать работу УУ на этапе процесса установления соединения и при проектировании новых КС.

Рассмотрим метод оценки среднего числа ПУС в предположении, что в качестве КС используется однородная разделенная многозвенная КС, работающая в режиме ГИ [4.5].

Основные определения На рис. 4.5 представлена КС, имеющая N входов и М выходов, которые разбиты на Н направлений по (/? = 1, Н) каналов в каждом направлении. Между каждым входом и выходом КС имеется совокупность соединительных путей (СП), образующих так называемый граф СП, конфигурация которого определяется структурой КС.

Если КС работает в режиме ГИ, то предполагается, что есть возможность подключения к любому каналу рассматриваемого направления.

Очевидно, что максимальное число подключений или опробований для некоторого направления А не может превышать числа каналов в этом

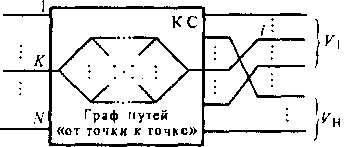
Рис. 4.5. Схема КС с ограниченным числом ПУС

направлении, т. е. V/,. При каждом подключении необходимо найти свободный СП между входом, по которому поступил вызов (на рис. 4.5 вход К), и определенным свободным выходом данного направления (на рис. 4.5 выход /). Выбор этого пути осуществляется путем просмотра ребер графа СП. Операцию поиска свободного СП между фиксированными входом и выходом будем называть попыткой установления соединения.

В современных квазиэлектронных и электронных КС для оптимизации работы УУ число ПУС ограничено некоторой величиной v < V. Она может быть выбрана как постоянной для конкретно рассматриваемой КС, так и переменной, зависящей от структуры КС, емкости пучка каналов в направлении искания, нагрузки, поступающей на это направление, и допустимой вероятности потерь.

Обозначим через Рь{ 1) вероятность блокировки вызова между определенными входом и выходом КС. Будем считать, что эта вероятность одинакова для любой пары вход-выход. Современные методы теории телетрафика [4.1, 4.6, 4.11] позволяют определить Р_ь( 1) с приемлемой для инженерной практики точностью для графа СП с достаточно произвольной структурой. Будем считать, что вероятность P_h( 1 ) известна. В общем случае, когда есть

i «S 1 свободных каналов в направлении искания, существует вероятность того, что вызов, поступивший на некоторый вход, окажется заблокированным ДЛЯ любого ИЗ i свободных ВЫХОДОВ. Обозначим эту вероятность Pb(i). Методы определения P_b(i) подробно рассмотрены в [4.1, 4.11, 4.13].

Введем обозначение [дс]_и(x = 0,V_h) - вероятность занятия х каналов в пучке V_h. Современные КС являются системами значительной структурной сложности и поэтому значение [x]_vможно найти лишь приблизительно.

В дальнейшем для определения вероятностей Pb{ï) и [x]_vбудем использовать метод раздельных потерь [4.1].

Определение среднего числа попыток установления соединения v

В квазиэлектронных и электронных КС работа УУ организована, как правило, таким образом, что поиск свободного СП между фиксированным входом и выходом осуществляется при наличии хотя бы одного свободного канала в рассматриваемом направлении. Вероятность этого события Р,= (4-60)

Вероятность блокировки вызова при первой попытке равна P_b( 1). С вероятностью ДО) последует вторая ПУС, при этом, если вероятность блокировки этого вызова P_h(2), то соединение будет установлено при двух по пытках с вероятностью [1 - /^>4(2)]/^> (,(1). Тогда по аналогии вероятность установления соединения при 1-й попытке

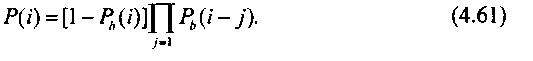
Формула (4.61) справедлива для /' = 1, у при РьФ) - 1.

Реализация каждой ПУС требует определенной затраты производительности УУ. Таким образом, вероятность Р_Ь{И) можно трактовать как значение затрачиваемой производительности УУ, выраженное в относительных единицах, при 1-й попытке. Однако УУ не всегда реализует у попыток установления соединения для подключения к направлению искания. С вероятностями Р_ь(\), Р_ь(2), Р_Ь(Ъ),…, /£(/),…,/£ (у) УУ осуществляет подключение с 1-,

2-, 3-, /'-й и и-й попыток. В среднем же для подключения к направлению искания УУ делает всего попыток

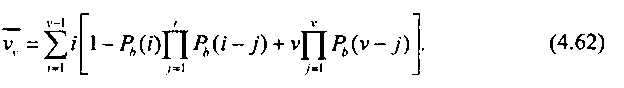
Выражение (4.62) справедливо для отдельных, фиксированных состояний пучка У,„ при которых в нем имеется не менее V свободных линий. Последнее слагаемое выражения (4.62) учитывает то обстоятельство, что подключение может и не произойти из-за внутренних блокировок в КС при у-й ПУС.

В общем случае осуществление / попыток зависит от состояния пучка У_и. Действительно, если рассматриваемый пучок V/, пребывает в состоянии х, то / попыток установления соединения можно реализовать, если У_л-х > /. Тогда выражение для среднего числа ПУС можно записать путем усреднения возможного числа попыток по отдельным состояниям пучка при условии, что в нем имеется по крайней мере одна свободная линия:

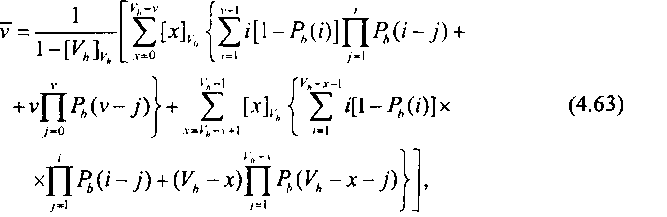
где Р_ь{0) = 1. В частном случае для режима ГИ, когда v = V_h, выражение

(4.63) упрощается и принимает вид

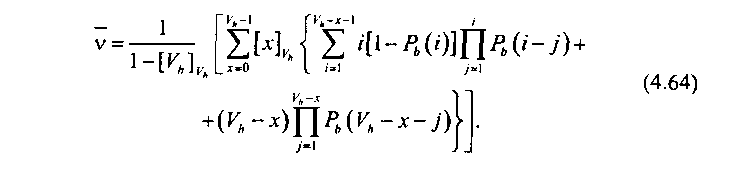
Формулы (4.63) и [4.64) связывают среднее число ПУС со структурными и нагрузочными параметрами КС. Проанализируем эти выражения.

С увеличением загрузки КС средняя нагрузка, обслуженная одной промежуточной линией, возрастает и стремится к единице: у^ -* 1. При этом увеличивается вероятность внутренних блокировок в КС, причем

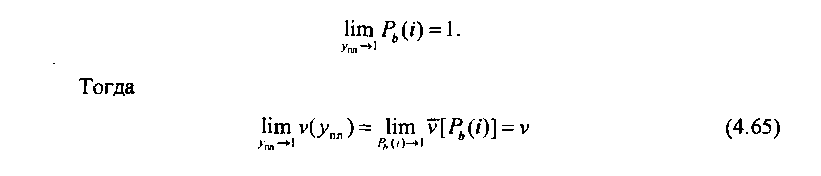
при условии, что у_т- удельная нагрузка, обслуженная направлением искания. В случае малой загрузки КС

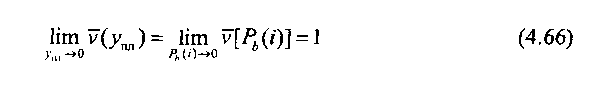
при Y = const.

Исследуем зависимость среднего числа ПУС от изменения величины нагрузки, обслуженной направлением искания. При этом [х]^ - f_x(Y_h) и

P_b(i) = /₂(У_Л). Функции^ и/2 имеют сложный нелинейный характер, поэтому исследование зависимости v = f(Y_h) проводилось численно по формуле (4.63). Результаты расчетов для 3-звенной КС с V_h= 10 показаны на рис. 4.6. При расчетах принималось, что число ПУС v = 5 и нагрузка, обслуженная одной промежуточной линией, Упл = 0,6 Эрл.

Анализ численных исследований показывает, что при малых значениях у_нвеличина среднего числа ПУС зависит от у_пп, обусловлена потерями из-за внутренних блокировок и численно равна [4.5]:

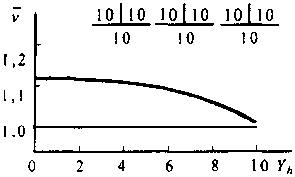
Рис. 4.6. Зависимость среднего числа ПУС от обслуженной нагрузки в направлении искания

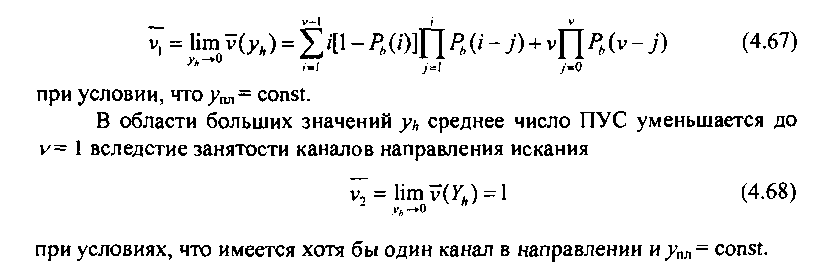
Сравнение результатов расчета и имитационного моделирования Поскольку выражение (4.63) является приближенным, то для определения области его применения было проведено имитационное моделирование КС в режиме ГИ с ограниченным числом попыток установления соединения. Моделирование и теоретический расчет по формуле (4.63) были выполнены для трехзвенной КС указанной выше структуры (см. рис. 4.6). Алгоритм поиска свободной промежуточной линии предполагался случайным, поток поступающих вызовов - поток от конечного числа источников нагрузки с интенсивностью а на каждом входе системы. Время обслуживания - экспоненциальное с интенсивностью р. = 1.

На рис. 4.7, а представлены расчетные зависимости V от удельного использования одной промежуточной линии упл для двух значений V = 2 (кривая 7) и у= 5 (кривая 2). Данные, полученные в результате имитационного моделирования, приведены в виде отдельных точек совместно с 95 %-ными доверительными интервалами.

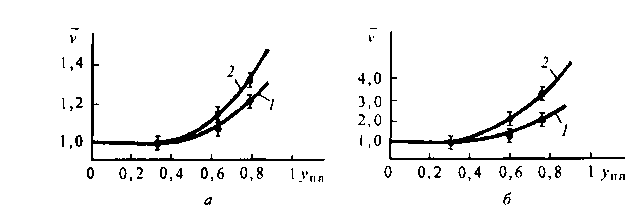
Рис. 4.7. Зависимость среднего числа попыток установления соединения от изменения удельной нагрузки на промежуточную линию:

/ - у = 2,2 - у= 5; а - 3-звенная КС, б - 6-звенная КС; I - результаты имитационного моделирования совместно с 95 %-ными доверительными интервалами

Анализ рис. 4.7 показывает, что теоретические кривые для обеих КС хорошо согласуются с данными имитационного моделирования во всем диапазоне значений у_т, встречающихся на практике, что подтверждает приемлемость принятых допущений, связанных с приближенным определением вероятностей Рь(0 и [х]_УНпри выводе формулы (4.63). Эти допущения - предположения о пуассоновском потоке вызовов и экспоненциальном времени обслуживания, причем каждая ПУС является независимым событием.

Формула (4.63) была использована для анализа эффективности алгоритмов установления соединения в системе коммутации с Fj = 0,8. Среднее число ПУС v определялось для АМТСКЭ емкостью N = 4096 вх/вых, причем при расчетах считалось, что в каждом направлении искания максимальное число ПУС v_max= 4.

На рис. 4.8 представлены зависимости среднего числа ПУС v от изменения величины обслуженной нагрузки у_плна промежуточную линию КС. Расчеты выполнены для фиксированного числа каналов направления искания V_h= 10 и двух значений величины нагрузки, обслуженной рассматриваемым направлением. Анализ кривых показывает, что в рекомендуемой области загрузки системы (у^ < 0,6 Эрл) v носит почти линейный характер, слабо возрастая с увеличением у_пл, но резко возрастает и имеет существенно нелинейную зависимость в области перегрузки системы (у„л > 0,6 Эрл).

Среднее число ПУС v существенно зависит от нагрузки Y_h, обслуженной направлением искания. На рис. 4.9 приведена эта зависимость при фиксированных емкости пучка каналов V_h- 10 и нагрузке на промежуточную линию ^пл = 0,6 Эрл. Анализ графика показывает, что при увеличе-

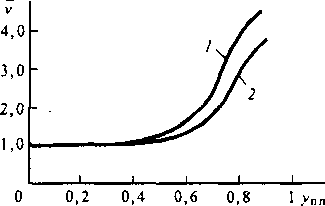
Рис. 4.8. Зависимость среднего числа ПУС от изменения обслуженной нагрузки на промежуточную линию при различных обслуженных нагрузках пучком каналов:

/ - ¥>,= 4,46 Эрл; 2- Г* = 7,74 Эрл

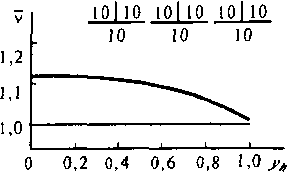
Рис. 4.9. Зависимость среднего числа ПУС от изменения удельной обслуженной нагрузки в направлении связи нии нагрузки, обслуженной направлением искания, среднее число ПУС уменьшается, поскольку уменьшается и число свободных выходов в направлении искания, следовательно, у УУ остается меньше возможности для реализации ПУС.

Разработанный метод определения среднего числа ПУС применим при проектировании как квазиэлектронных, так и электронных КС. Использование этого метода позволяет оптимизировать работу УУ с учетом структуры станции, ее загрузки, емкости пучков каналов в направлении искания и нагрузок, обслуживаемых этими направлениями. Проведенная экспериментальная проверка предложенного метода показала возможность его применения в широком диапазоне структурных и нагрузочных параметров КС.

⇐Влияние числа попыток установления соединения на пропускную способность узла коммутации | Мультисервисные телекоммуникационные сети | Математическая модель узла коммутации цсис с учетом влияния повторных вызовов⇒