Исследуем характеристику КС, которая, как будет показано ниже, полезна при расчете емкости пучков каналов в направлениях искания КС. Рассмотрим отношение эффективной доступности к числу каналов в направлении искания. Назовем это отношение коэффициентом доступности и будем обозначать

Коэффициент доступности характеризует степень близости КС к неблокируемой системе. Очевидно ^ < 1. Ограничиваясь при расчете ЭД приближением второго порядка, коэффициент доступности в направлении г имеет вид

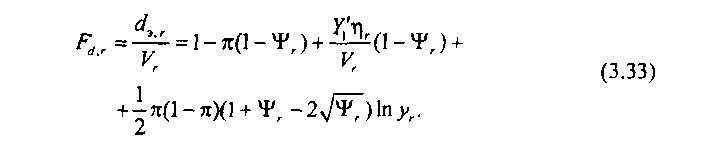
Проанализируем выражение (3.33). При проектировании узлов и станций сети связи допустимая загрузка системы является заданной, т. е. можно принять, что параметр тс, входящий в (3.33), является постоянным. Учитывая, что реальные узлы и станции имеют обычно достаточно большую емкость и большое число направлений, т. е. параметры г\_ги ЧР_Г, являясь функциями емкости пучков, оказываются величинами весьма малыми. Это означает, что влияние их на значение коэффициента доступности последних двух слагаемых, входящих в (3.33), незначительно. Следовательно, при указанных условиях коэффициент доступности есть функция, слабозавися-щая от емкости пучка каналов в направлении искания. Эту особенность коэффициента доступности можно использовать при расчете емкости пучков каналов в направлениях искания в многоканальных системах. В этих системах выполняются указанные выше условия и коэффициент доступности при фиксированной ее загрузке можно рассматривать как инвариант системы.

Таблица 3.1

О характере зависимости коэффициента доступности ^ от емкости пучка У_ги коэффициента тяготения г_гможно судить по двум примерам. Первый пример относится к трехзвенной КС со следующей структурой:

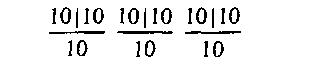
КС работает в режиме группового искания, при этом h = V_r= V = 10; T_r=0,1, r = \,h. Условия работы системы таковы, что коэффициент тяготения в каждом направлении различен. Общая нагрузка, обслуженная КС, составляет У = 56,1 Эрл. Результаты расчета коэффициента доступности F_dдля каждого направления искания при соответствующем значении коэффициента тяготения г)_гприведены в табл. 3.1. Здесь же представлены значения вероятности потерь в каждом направлении, полученные путем статистического моделирования системы с 95 %-ми доверительными интервалами [3.4]. Анализ данных табл. 3.1 показывает, что при изменении коэффициента тяготения примерно в 2,4 раза, что соответствует изменению вероятности потерь Р от 0,008 до 0,609, коэффициент доступности F_dизменяется менее чем на 2,5 %.

Второй пример относится к четырехзвенной КС со следующей структурой:

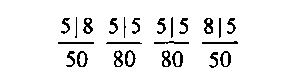
КС работает в режиме группового искания, при этом А = 5. Данные о емкостях пучков каналов и коэффициентах тяготения в каждом направлении приведены в табл. 3.2. Общая нагрузка, обслуженная системой, составляет У= 199,91 Эрл. Результаты расчета коэффициента доступности Ра и значения вероятности потерь для каждого направления искания, полученные путем статистического моделирования системы [3.4], представлены в табл. 3.2. Анализ данных табл. 3.2 показывает, что при изменении емкости пучков от 25 до 100 каналов, коэффициента тяготения в 4,75 раза и вероятности потерь от 0,0004 до 0,45 коэффициент доступности Ра изменяется менее чем на 3,5 %.

Таблица 3.2

В рассмотренных примерах емкость первой КС составляла 100, второй - 250 входов/выходов. Реальные узлы и станции имеют значительно большую емкость, которая может достигать нескольких десятков тысяч каналов. Поэтому можно ожидать, что варьируемость коэффициента доступности в таких системах в зависимости от емкости пучков будет еще меньшей.

Значительная устойчивость при варьировании в широких пределах емкости пучков каналов и нагрузок в направлениях искания делает этот параметр важной характеристикой узла коммутации. Знание коэффициента доступности КС позволяет упростить расчет емкости пучков каналов в системах, характеризующихся значительной структурной сложностью. Заметим, что если для фиксированной загрузки КС и заданной нормы потерь известна величина /V, то тем самым однозначно определена связь между емкостью пучка V и эффективной доступностью ^_э. Учет этого обстоятельства позволяет сократить перебор и построить целенаправленную процедуру расчета емкости пучков.

Кроме рассмотренного аналитического метода определения коэффициента доступности, его можно найти по данным имитационного моделирования. В этом случае по заданной нагрузке, емкости пучка каналов в направлении искания и найденной в результате моделирования вероятности потерь из (3.7) определяется ЭД, а затем - коэффициент доступности Эффективная доступность и коэффициент доступности использованы в [3.7] при расчете вероятностных характеристик многокаскадных КС, работающих в режиме группового искания и в режиме искания «от точки к точке». Вопрос применения изложенного метода определения ЭД будет рассмотрен в следующих главах, посвященных расчету вероятностных характеристик систем МК и систем МК с канальным резервированием (МК КР).

Литература 3.1. Ершов В.А. Средняя доступность и рекуррентный расчет потерь в коммутационных системах // Автоматы и управление. Системы управления сетями. М.: Наука, 1980. С. 121-126.

3.2. Ершова Э.Б., Ершов В.А. Цифровые системы распределения информации. М.: Радио и связь, 1983.

3.3. Харкевич А.Д. Приближенный метод расчета числа соединительных устройств в АТС координатной системы // Электросвязь. 1959. № 2. С. 55-63.

3.4. Bazlen D., Катре G., Lotze A. On the Influence of Hunting Mode and Link Wiring on the Loss of Link System // 7 IT С Stockholm, 1973. P. 232/1-232/12.

3.5. BinindaH., Wendt A. Die effective Erreichbarkeit fur Abnehmerbundel hinter Zwischenleitungs Anordnung//NTZ, 1959. N. 12. S. 579-585.

3.6. Brockmeyer E., Hallstrom H.L., Jensen A. The Life and Works of A.K. Erlang. Acta Polytechnica Scandinavica Math. Copenhagen, 1948.

3.7. Ershov V., lgelnikM. A Grade of Service Analysis for Multi-Channel Switching in ISDN // ITC-13, Copenhagen, June 19-26,1991. P. 891-898.

3.8. Ershov V., YershovD. Modelling and traffic analysis of a multi-channel trunk reservation switching system // Third German-Soviet Seminar on Flow Control Communication System. Dortmund. October 9-15, 1991. University of Dortmund. Institute for Electronic Systems and Switching.

3.9. Kummerle K. Berechnungsverfahren fur mehrstufige linebreak Koppelanordnungen Konjugerter Durchschaltung // Systematik und Analyse. 9 Berict uber verkehrstheoretische Arbeiten. Institute of Switching and Data Technics. University of Stuttgart, 1969. P. 263.

3.10. Lotze A. 3.Bericht tiber verkehrstheoretische Untersuchungen (C1RB). Stuttgart. 1NVDVTH, 1963.

3.11. Lotze A., Roeder A., Thierer G. NIK-Charts for the Design of Link System operating in the Point-to-Point Selection Mode or Point-to-Group Selection Mode. Institute of Switching and Data Technics. University of Stuttgart, 1976.

3.12. Lotze A., Rothmaier K„ SchellerR. PCM-Charts for the Design of Economic PCM Switching Arrays operating in the Point-to-Point Selection Mode. Institute of Switcing and Data Technics. University of Stuttgart, 1979.

3.13.Pedersen O.A. An Effective Availability Theory with Application // IEEE Trans, on Com. Vol. Com-23. N. 8, 1975. P. 798-803.

«Цель расчетов - не числа, а понимание» Р.В. Хемминг

⇐Дисперсия и начальные моменты распределения доступности | Мультисервисные телекоммуникационные сети | Вероятностные характеристики систем многоканальной коммутации⇒