В гл. 4 и 5 рассмотрены методы расчета вероятностных характеристик КС. Важным этапом этих методов является этап расчета эффективной доступности КС. Как будет показано в гл. 3, для определения эффективной доступности КС необходимо вычислить вероятность блокировки выхода системы к. Для этого можно использовать вероятностные графы, описывающие систему, работающую в режиме искания «от точки к точке». Кроме того, исследование рассматриваемых пространственно-временных систем при одноканальной коммутации в режиме искания «от точки к точке» представляет самостоятельный интерес. Вероятность внутренних блокировок в многокаскадной схеме зависит от режима искания и способа включения промежуточных линий.

Соединительные пути, которые можно использовать в процессе искания, изображают в виде графа. Дуги графа соответствуют промежуточным линиям и выходам, а вершины - коммутаторам. Для рассматриваемых 3-каскадной КС типа В-П-В, 4-каскадной КС типа В-П-П-В, 5-каскадной КС типа В-П-П-П-В и 6-каскадной КС типа В-П-П-П-П-В графы возможных соединительных путей приведены на рис. 2.10, а-ж.

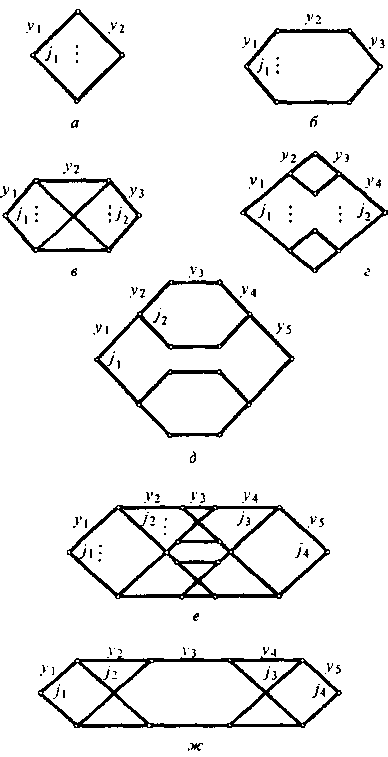
Рис. 2.10. Вероятностные графы простран-ственно-временных КС

Задача искания в многокаскадной КС состоит в определении пути, для которого все последовательно включенные промежуточные линии и выход одновременно свободны. Каждая линия с определенной вероятностью может быть в состоянии занятости. Если придать каждой дуге в графе вес, равный вероятности занятости той линии, которую данная дуга представляет, то граф приобретает вероятностный смысл. Подобный граф называется вероятностным. Вероятностный граф удобно применять для онределения потерь в многокаскадных схемах, поскольку он достаточно детально отражает структуру и режим работы коммутационного поля.

Метод вероятностных графов, предложенный в [2.3], основан на следующих двух предположениях:

• независимости занятия последовательно включенных линий пути;

• независимости состояний любой из этих линий.

Исходя из этих предположений, состояния двух любых дуг некоторого графа можно считать независимыми друг от друга. Это равносильно предположению о справедливости биномиального распределения для вероятностей занятости ребер на всех звеньях КС. Такая гипотеза может быть принята для КС достаточно большой емкости.

В простейшем случае граф состоит только из одной дуги с вероятностью занятости у, равной интенсивности нагрузки, которая обслуживает линию, характеризуемую этой дугой (рис. 2.11, а). Вероятность потерь в таком графе составляет

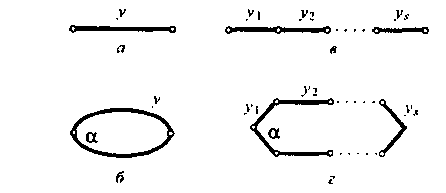
Рис. 2.11. Параллельно-последовательные вероятностные графы

Вероятность потерь в графе, состоящем из а параллельно включенных дуг (рис. 2.11, б),

Вероятность потерь в графе (рис. 2.11, в), состоящем из ^ последовательно включенных дуг с вероятностями занятости у,,у₂,--,у/-

Граф (рис. 2.11, г), представляющий только параллельно-последовательное включение дуг, называют графом типа П. Вероятность потерь в таком графе

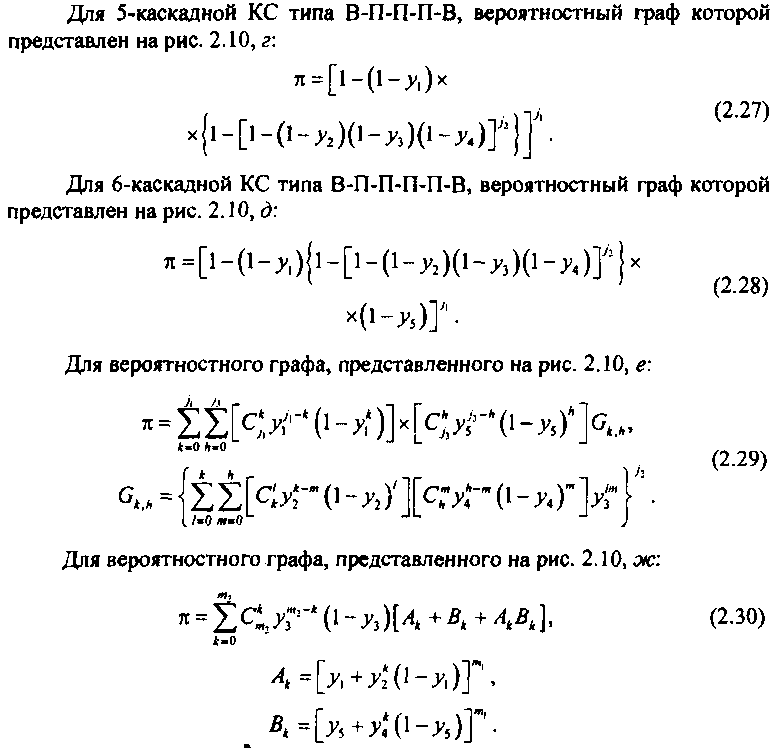
Использование вероятностей блокировки л для расчета вероятностных характеристик систем многоканальной коммутации будет подробно рассмотрено в гл. 3.

Литература 2.1. Ершов В.А. Коммутация на интегральной цифровой сети связи. М.: Связь, 1978.

2.2. Ершова Э.Б., Ершов В.А. Цифровые системы распределения информации. М.: Радио и связь, 1983.

2.3. Lee C.Y. Analysis of Switching Networks // BSTJ. N. 34, 1955. P. 1287-1315.

2.4. LotzeA., Rothmaier K„ Scheller R. PCM-Charts for the Design of Economic PCM Switching Arrays operating in the Point-to-Point Selection Mode. Inst, of Switching and Data Technics University of Stuttgart, 1979.

«Дьявол прячется в деталях» Английская пословица 3. ЭФФЕКТИВНАЯ ДОСТУПНОСТЬ КОММУТАЦИОННЫХ СИСТЕМ

⇐Оценка сложности структуры коммутационных систем | Мультисервисные телекоммуникационные сети | Асимптотическая оценка эффективной доступности⇒