Сетевая модель отображает взаимосвязи между операциями и порядок их выполнения. Как правило, используется следующая символика:

♦ операция представляется в виде ориентированной дуги (т. е. дуги со стрелкой);

♦ упорядочение между операциями задаётся с помощью событий. Событие - это момент времени, когда завершается одна операция и начинается следующая. Таким образом, каждая операция ограничена своими начальным и конечным событиями.

Правила построения сетевой модели: Правило 1. Каждая операция в сети представляется только одной дугой.

Правило 2. Ни одна пара операций не должна определяться одинаковыми начальным и конечным событием. Чтобы избежать подобной неопределённости, а также задать в ряде случаев отношения упорядоченности, вводят фиктивные операции.

Правило 2 иллюстрируется на рис. 4.2а и рис. 4.26.

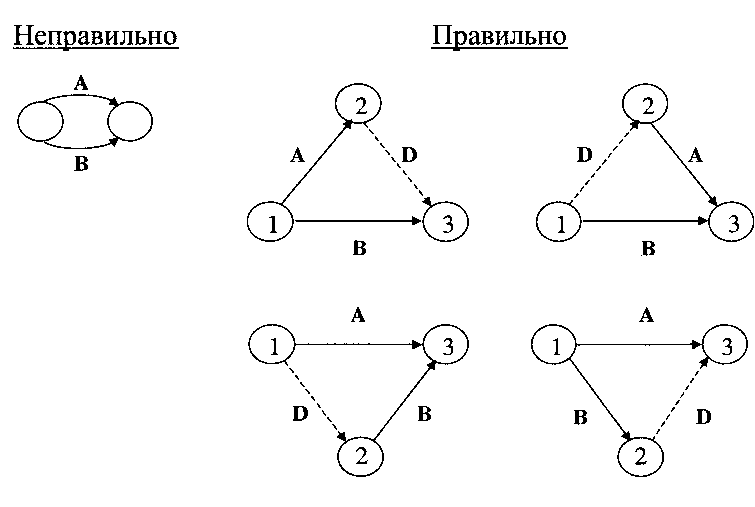
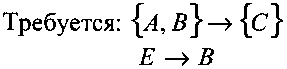
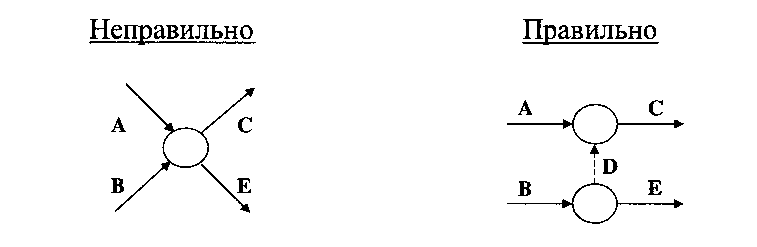
Рис. 4.26

Правило 3. При включении операции в сетевую модель для обеспечения правильного упорядочения необходимо ответить на вопросы:

a) какие операции необходимо завершить непосредственно перед началом данной операции?

b) какие операции должны непосредственно следовать после завершения данной операции?

c) какие операции могут выполняться одновременно с данной операцией?

На рис. 4. 3 показан пример сетевой модели.

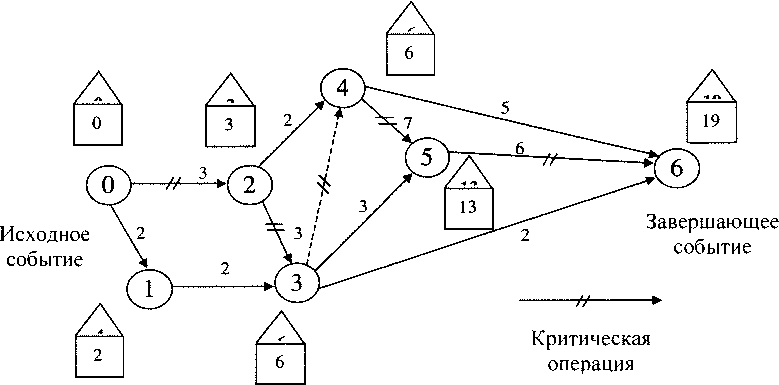
Рис. 4.3

4.3. РАСЧЁТ СЕТЕВОЙ МОДЕЛИ

В ходе расчёта определяются критические и некритические операции проекта. Операция считается критической, если задержка её начала приводит к увеличению срока окончания всего проекта. Критический путь определяет непрерывную последовательность критических операций, связывающих исходное и завершающее событие. Некритическая операция имеет резерв (запас) времени, поскольку промежуток времени между её ранним началом и поздним окончанием больше её длительности.

Расчёт критического пути включает два этапа. Первый этап - прямой проход. Вычисления ведутся от исходного события до завершающего. Определяются ранние сроки наступления событий £5,, где г - индекс события. Обозначим символом Ду продолжительность операции (г, /). Основная формула для вычисления при прямом проходе для всех операций (г, /).

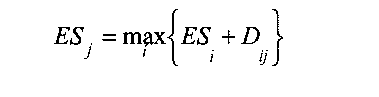
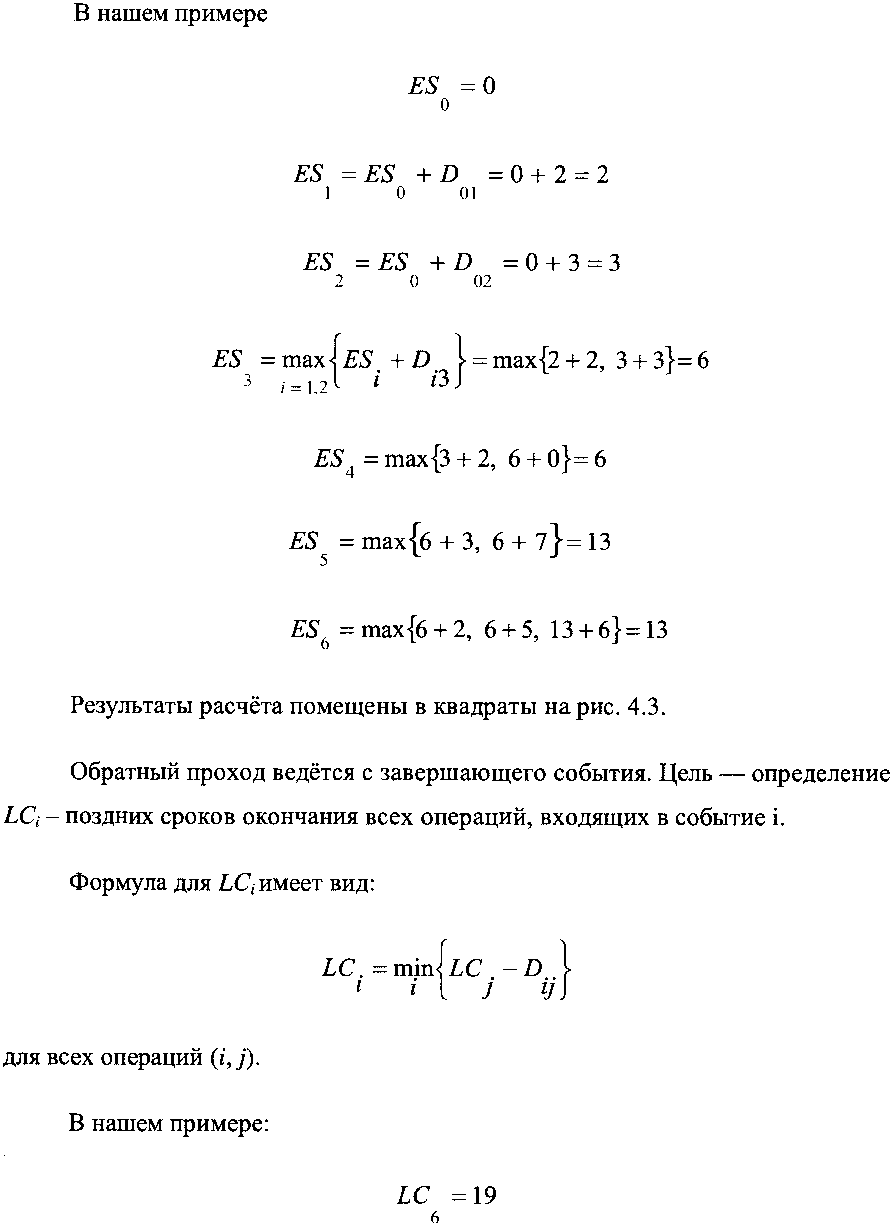
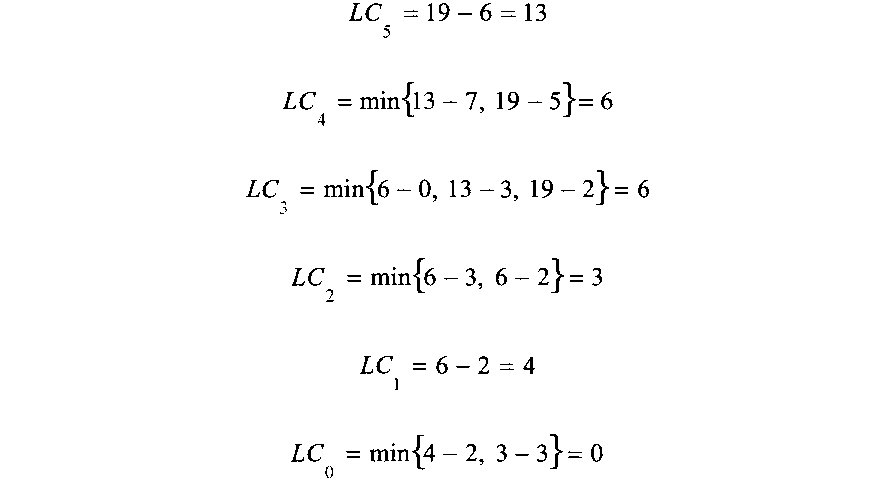
Результаты записаны в треугольниках рисунка 4.3. Операция является критической, если:

♦ для начального события ранний срок начала и поздний срок окончания совпадают;

♦ то же самое и для конечного события;

♦ разница между сроками начального и конечного события равна длительности операции.

Критические операции в примере - (0,2), (2,3), (3,4), (4,5), (5,6).

Для некритических операций вычисляются резервы времени. Различают два основных вида резервов времени:

1. Полный резерв. Он определяется соотношением: Полный резерв = (позднее время завершения операции - ранее время начала операции) - длительность операции, т. е.

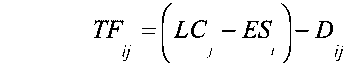
2. Свободный резерв. Он определяется в предположении, что все операции в сети начинаются в ранние сроки (т. е. имеется в виду левое крайнее расписание работ).

Свободный резерв определяется как превышение допустимого отрезка

/ Л

времени работы ЕБ - ЕБ над её продолжительностью:

I ' Ч

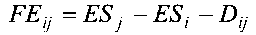
У критических операций полные и свободные резервы равны нулю. У некритических операций полные резервы не равны нулю, а свободные резервы могут принимать как ненулевые значения, так и нулевые значения.

В примере получены следующие результаты:

⇐Проекты, программы и их место в erp | Система управления предприятием типа ERP | Построение календарного графика и распределение ресурсов⇒