Количественные методы прогнозирования реализуются с помощью математических моделей, базирующихся на предыстории. Подобные модели строятся в предположении, что данные о поведении процесса в прошлом могут быть распространены и на будущее.

Количественные методы представляют собой довольно развитую область, поэтому в данном пособии рассматриваются только некоторые модели, наиболее часто включаемые в базовые системы и пакеты прикладных программ. Все они основаны на временных рядах, полученных путём измерений в определённых временных периодах.

Одна из центральных проблем - оценка и повышение точности прогнозов. Фактическая точность может быть оценена только путём сравнения прогностических и фактических данных. Если точность модели недостаточна, то метод модифицируется или заменяется.

Хотя внешне результаты измерений (особенно долгосрочных) могут выглядеть хаотичными, в них можно выявить довольно простые составляющие.

На рис. 3.3 показано, как данные об объёмах продаж в прошлом могут быть разложены на несколько компонент.

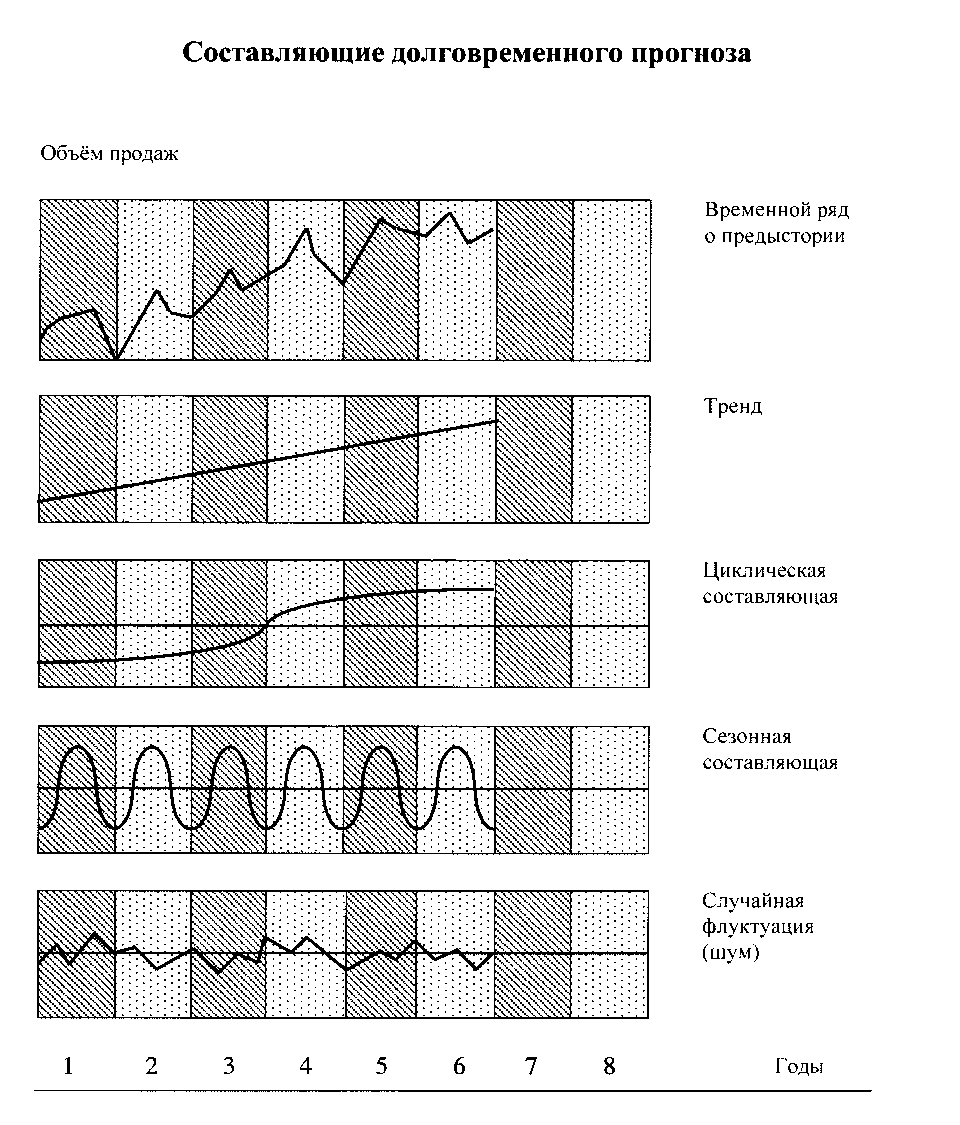
Рис. 3.3

Тренд представляет собой постоянную, долговременную тенденцию.

Циклическая составляющая описывает ту часть процесса, которая повторяется с низкой частотой.

Сезонная составляющая описывает циклы, повторяющиеся с высокой частотой раз в течение года.

Периоды циклической и сезонной составляющих могут находиться между собой в определённых отношениях. Примеры отношений приводятся ниже.

Период цикличности Период сезонности Количество сезонов в цикле

Случайная флуктуация представляет собой случайное отклонение временного ряда от неслучайной функции, описываемой трендом, циклической и сезонной составляющими.

Прогнозирование на основе количественных методов заключается прежде всего в определении вида и параметров функций, описывающих неслучайные составляющие.

Наиболее часто применяется следующие количественные модели прогнозирования.

1. Линейная регрессия. Модель направлена на выявление связи между зависимой переменной (т. е. прогнозируемой величиной) и одной или более независимыми переменными, которые представлены в виде данных о предыстории. В простой регрессии имеется только одна независимая переменная, а в множественной регрессии их несколько. Если предыстория представлена в виде временного ряда, то независимая переменная - это временнЬй период, а зависимая -прогнозируемая величина, например, объём продаж. Регрессионная модель не обязательно базируется на временных рядах. В этом случае представления о величинах независимых переменных используются для того, чтобы определить зависимую переменную. Линейная регрессия обычно используется для долгосрочных прогнозов, но может также применяться для менее длительных прогнозов.

2. Методы скользящего среднего. Прогностическая модель для краткосрочных прогнозов, основанная на временных рядах. В этой модели среднее арифметическое фактических продаж, вычисленное для принятого числа последних прошедших временных периодов принимается за прогноз на следующий временнЬй период.

3. Метод взвешенного скользящего среднего. Эта модель работает подобно предыдущей модели, но в ней вычисляется не среднее, а средневзвешенное значение, которое и принимается за прогноз на ближайший временной период. Меньшие веса приписываются более отдалённым периодам, отражая тем самым уверенность в том, что прогнозируемый процесс в ближайший период не претерпит резких изменений.

4. Экспоненциальное сглаживание. Также модель, использующая временные ряды и предназначенная для краткосрочных прогнозов. В этом методе объём продаж, спрогнозированный для последнего периода, корректируется на основе информации об ошибке прогноза в последнем периоде. Этот скорректированный за последний период прогноз и становится прогнозом на следующий период.

5. Экспоненциальное сглаживание с трендом. Эта та же модель, что и представленная выше, но модифицированная так, чтобы обрабатывать данные с трендами. Такие расчёты характерны для среднесрочного прогнозирования. Называется также моделью с двойным экспоненциальным сглаживанием, поскольку сглаживание выполняется для среднего значения и для тренда.

Следующим примером можно проиллюстрировать задачу прогнозирования на основе линейной регрессионной модели.

Требуется спрогнозировать количество продаж на ближайшие три года, если известны количества продаж по годам за последние 10 лет.

Математическая модель для линейной регрессии выглядит так: х - значение независимой переменной у - значение зависимой переменной п - число наблюдений в прошлом Г, X - величины зависимых и независимых переменных, принадлежащие линейной функции У = а + ЬХ, описывающей тренд а, Ь - коэффициенты г - коэффициент корреляции. Это величина, изменяющаяся от -1 до +1.

Она свидетельствует о степени зависимости у от * и о направленности этой зависимости.

Решение задачи состоит прежде всего в определении коэффициентов а и Ь.

Формулы (без вывода) выглядят следующим образом:

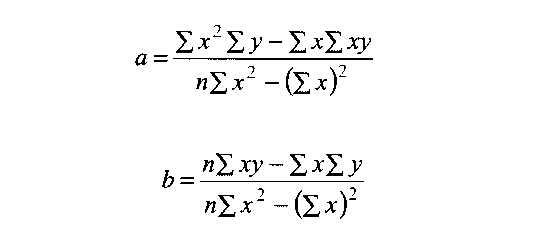
Эти формулы соответствуют методу наименьших квадратов. Смысл заключается в том, чтобы найти такую линейную функцию (т. е. коэффициенты а и Ь), для которой сумма квадратов отклонений между величинами у и У была бы минимальной.

Следующая таблица показывает шаги расчёта.

Коэффициенты аиЬ вычисляются следующим образом:

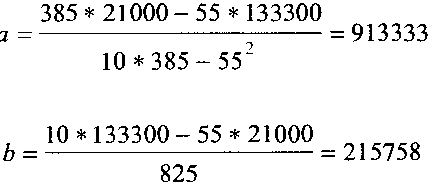
Таким образом, прогнозируемая величина описывается следующей функцией:

В качестве прогнозируемых величин можно принять их округление с точностью до десятков, например, Y_u= 3290, Y_n- 3500, Y₁₃= 3720.

⇐Каественные методы прогнозирования | Система управления предприятием типа ERP | Соетания прогнозирования и планирования⇒