Сущность линейного программирования и его роль в оптимизации и анализе экономической деятельности хорошо видны из примера, приведённого в книге X. Taxa «Введение в исследование операций».

Содержательная постановка задачи. Фабрика изготавливает два вида красок: для внутренних (I) и наружных (Е) работ.

Продукция обоих видов поступает в оптовую продажу. Для производства красок используются два исходных продукта - А и В. Максимально возможные суточные запасы этих продуктов составляют 6 и 8 т соответственно. Расходы А и В на 1 т соответствующих красок приведены в таблице.

Изучение рынка сбыта показало, что суточный спрос на краску I никогда не превышает спроса на краску Е более чем на 1 т. Кроме того, установлено, что спрос на краску I никогда не превышает 2 т в сутки.

Оптовые цены одной тонны красок равны: 3 тыс. долл. для краски Е, 2 тыс. долл. для краски I.

Какое количество краски каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?

Математическая модель включает переменные, ограничения, цель.

Переменные х_Еи х₁- суточные объёмы производства.

Целевая функция - максимум общего дохода.

Ограничения - на расход исходных продуктов, величину спроса на продукцию, неотрицательность объёмов производства.

Математическая модель шах г = Зх_Е+2х, х_Е+ 2х, < 6 2х_е+ х, < 8

- х_Е+ х_}<1 х, <2 х_Е>0, х, > О

Свойства линейной модели - пропорциональность и адаптивность.

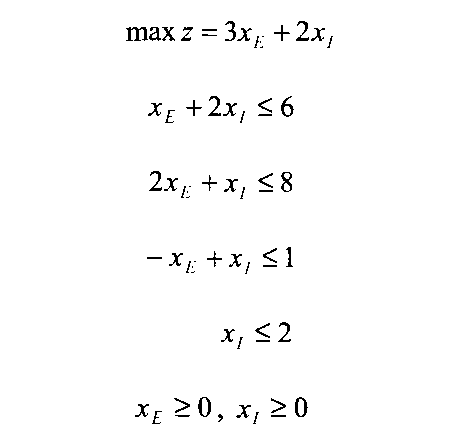
Область допустимых решений высекается ограничениями, как показано на рис. 7.

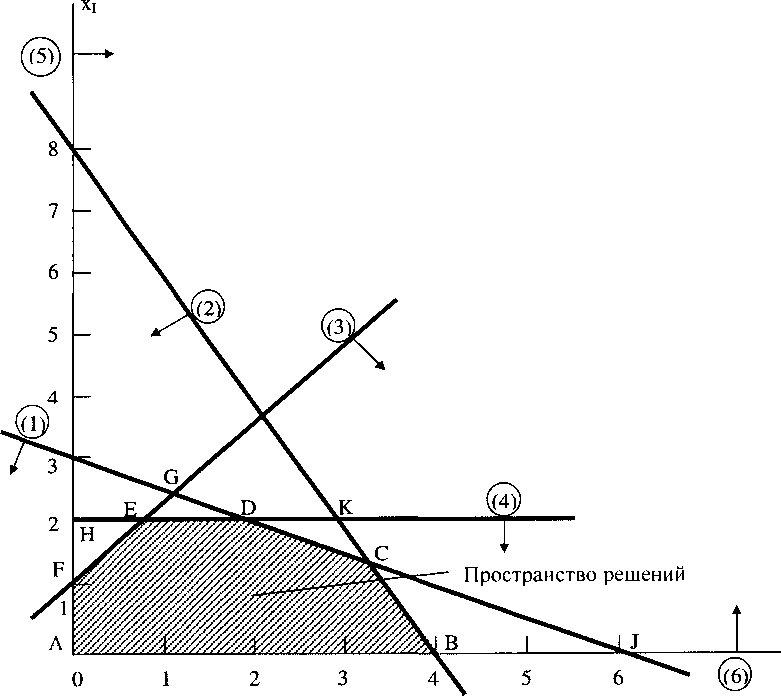
Рис. 7

Геометрическое решение задачи заключается в перемещении функции, характеризующей доход в направлении возрастания целевой функции до тех пор, пока она не выйдет за область допустимых решений.

Достижение оптимума показано на рис. 8.

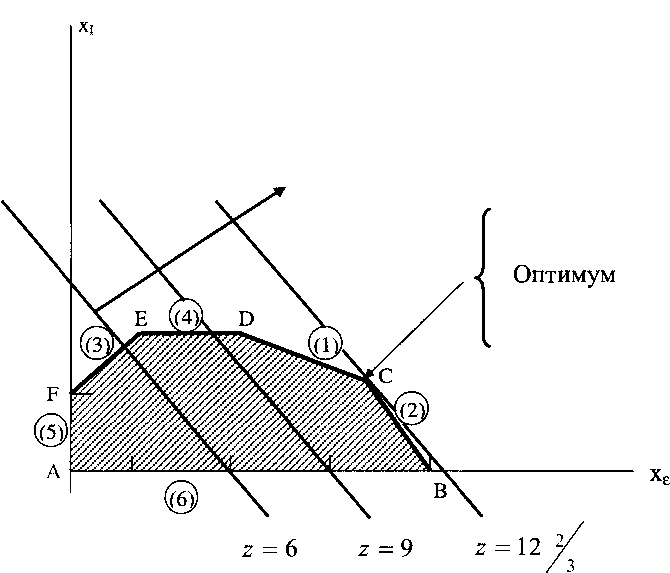
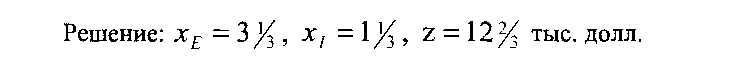
Рис. 8

Решение: х_Е=Ъ^х/_ъ, х₁= \^х/_ъ, ъ = \2^г/_ътыс. долл.

В ЛП оптимум - всегда в одном из углов многогранника допустимых решений.

Основной численный метод решения задачи ЛП - симплекс метод. Его суть заключается в обходе в определённой последовательности «углов» многогранника до достижения оптимального решения.

Ценность ЛП не только в том, что находится оптимальное решение, но и в том, что с его помощью выполняется анализ решения на чувствительность.

Первая задача анализа на чувствительность (чувствительность к правой части ограничений).

Есть два аспекта:

1. На сколько можно увеличить запас некоторого ресурса для улучшения полученного оптимального значения целевой функции?

2. На сколько можно снизить запас некоторого ресурса при сохранении полученного оптимального значения целевой функции?

Два типа ограничений:

1. Связывающие (активные) - соответствующие дефицитным ресурсам. Их касается первый аспект задачи.

2. Несвязывающие (неактивные) - соответствуют недефицитным ресурсам. Их касается второй аспект.

Влияние изменений дефицитных ресурсов показано на рис. 9, рис. 10 и рис. 11.

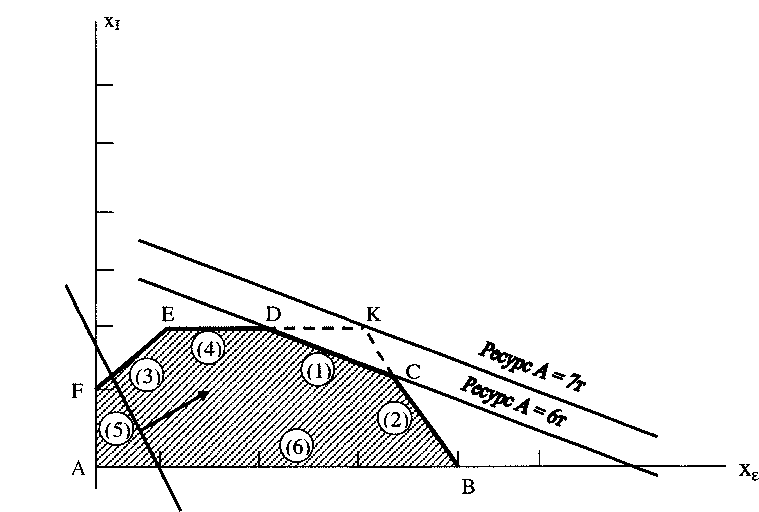
Рис. 9

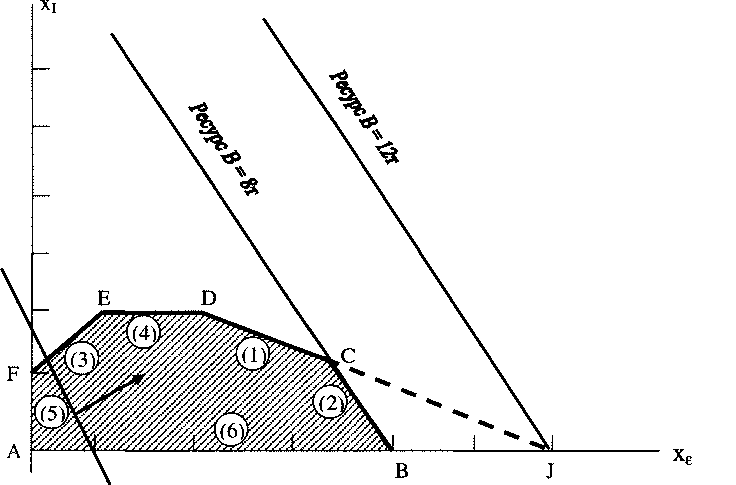
Вторая задача анализа на чувствительность. Увеличение объёма какого из ресурсов наиболее выгодно? Оценка ценности дополнительной единицы i-ro ресурса y_iвычисляется по формуле:

max Az

у. = тахДг Результаты для ограничений 1 -4 имеют вид:

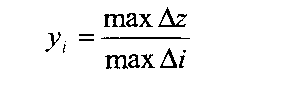
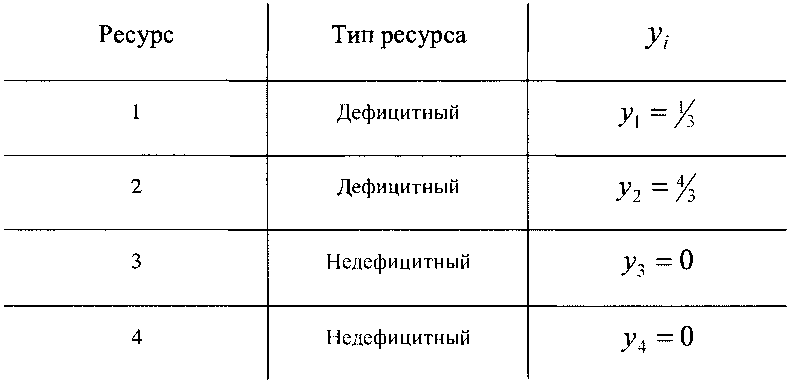
Вложения надо направлять прежде всего в ресурс 2 (продукт В), а затем в продукт А.

Третья задача анализа на чувствительность. В каких пределах допустимо изменение коэффициентов целевой функции?

Изменение коэффициентов целевой функции оказывают влияние на её наклон, а от этого зависит и точка оптимума.

Возникают два вопроса:

1. Каков диапазон изменения (увеличения или уменьшения) того или иного коэффициента целевой функции, при котором не происходит изменения оптимального решения?

2. Насколько следует изменить тот или иной коэффициент целевой функции, чтобы сделать некоторый недефицитный ресурс дефицитным и, наоборот, дефицитный ресурс сделать недефицитным?

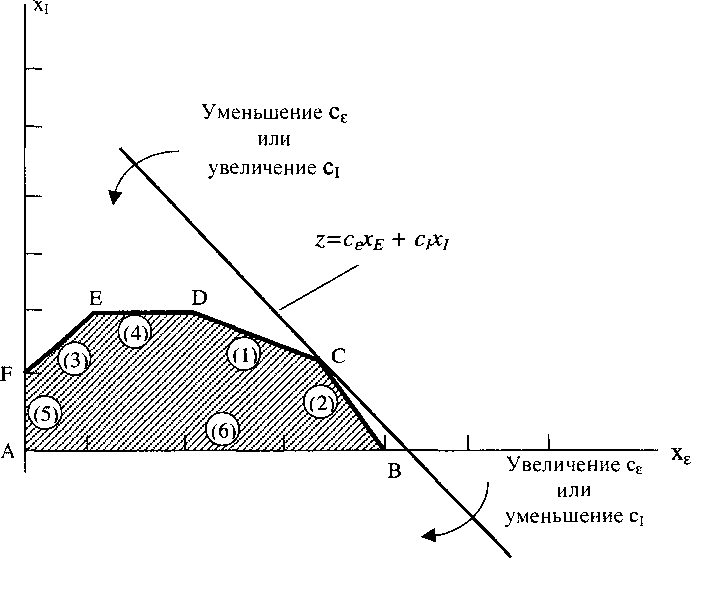
Пусть прямая вращается против часовой стрелки. Можно выделить следующие зоны:

1. Оптимальное решение не меняется.

2. Множественность решений.

3. Оптимально решение - точка Б.

Дефицитны ресурсы 1,4. Ресурс 2 недефицитный и т. д.

При С₁=2 1 < С_Е< 4

⇐Оптимальное планирование в арб | Система управления предприятием типа ERP | Метод слуайного поиска⇒