Календарный график получается путём преобразования результатов расчётов на сетевой модели в реальную временную шкалу. Для некритических операций на нём показаны ранние начала и поздние окончания.

График для примера показан на рис. 4.4.

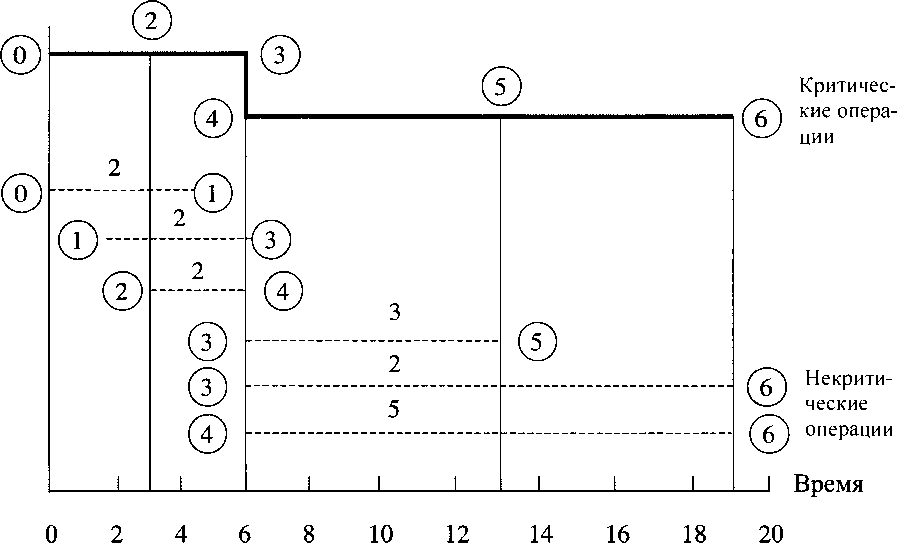
Рис. 4.4

Резервы важны, потому что сдвигая работы в рамках резервов можно добиться удовлетворения ограничений на ресурсы или добиться их наиболее равномерного условия. Сдвиг работ сопровождаться контролем за ситуацией на основе анализа свободного резерва. Если он меньше полного, то при выходе за свободный резерв будут затронуты последующие работы, иначе отношения следования нарушаются. При распределении ресурсов возникает многовариантная задача, которая может быть описана как оптимизационная. В ряде систем ERP и самостоятельных систем управления проектами имеются эвристические, т. е. нестрогие методы получения удовлетворительного решения задачи. Сущность задачи иллюстрируется рис. 4.5, рис. 4.6 и рис. 4.7.

На рис. 4.5 показаны потребности в ресурсах для крайнего левого расписания, а на рис. 4.6 - для крайнего правого расписания. В первом случае работы начинаются как можно раньше, а во втором завершаются как можно позднее.

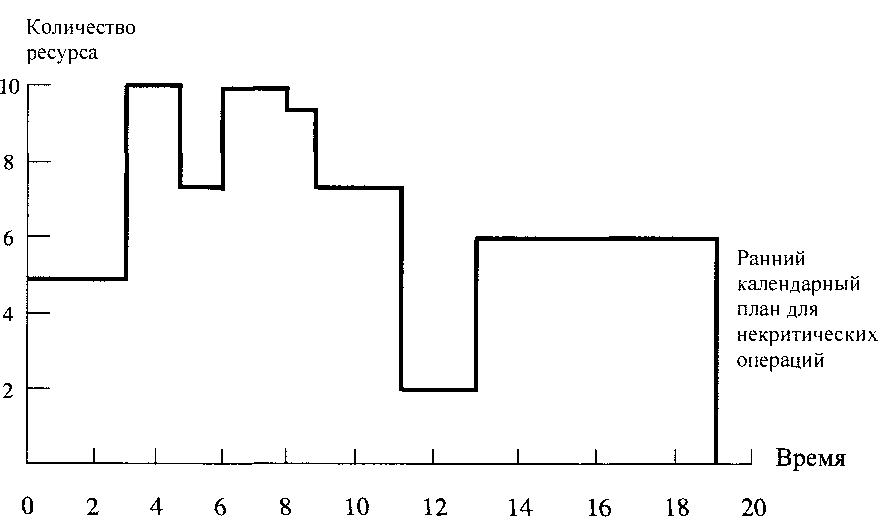
Рис. 4.5

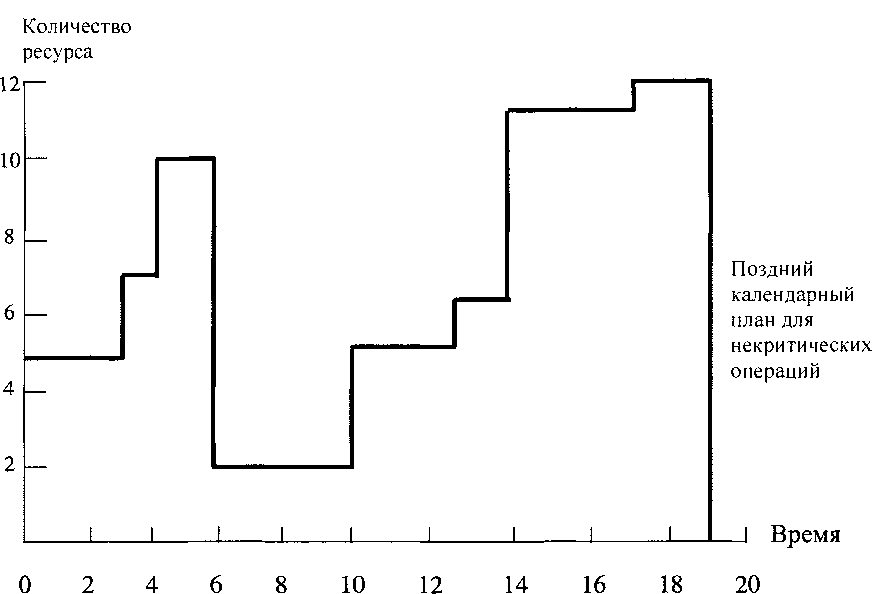
Рис. 4.6

В первом случае затраты ресурсов смещены влево, в во втором - вправо.

На рис. 4.7 показан промежуточный вариант, для которого характерно более равномерное использование ресурсов и снижение пиковых потребностей в ресурсах. Очевидно, этот график построен за счёт перемещения некритических работ в рамках резервов.

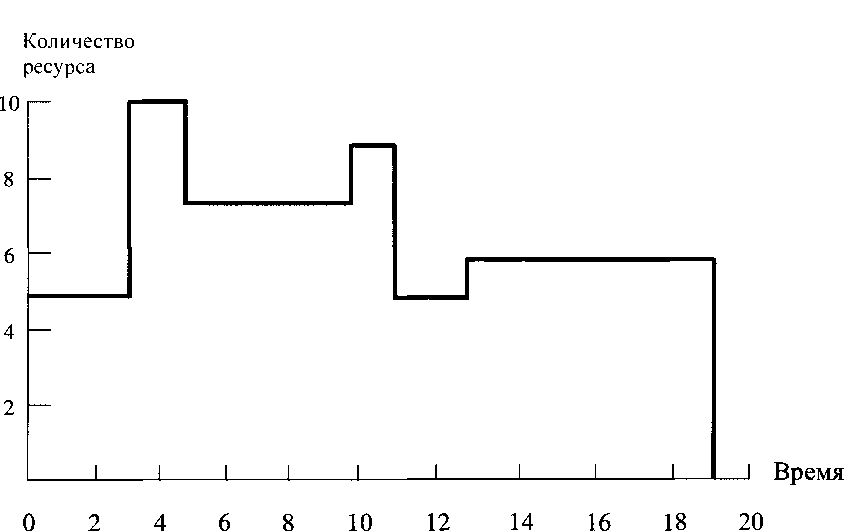
Рис. 4.7

4.5. УЧЁТ НЕОПРЕДЕЛЁННОСТИ И ЗАТРАТ ПРИ УПРАВЛЕНИИ ПРОЕКТОМ

В больших и длительных проектах, особенно на ранних стадиях их существования, может возникать неопределенность, прежде всего, временных оценок. В первую очередь это порождает вопрос о том, каковы вероятностные характеристики проекта.

Вероятностный характер процесса реализации проекта учитывается за счёт введения для каждой операции трёх оценок её длительности:

t₀- оптимистическая(минимальная) оценка;

t_p- пессимистическая (максимальная) оценка;

t_m- наиболее вероятная оценка.

Из этих трёх оценок получаются математическое ожидание t_eи дисперсия V по формулам:

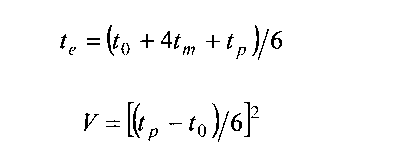
Три оценки для каждой операции позволяют вычислить характеристики нормального распределения - длительность и дисперсию для каждого пути в сети. Ожидаемая длительность равна сумме ожидаемых длительностей входящих в него операций, а дисперсия для длительности пути равна сумме дисперсий операций. В предположении нормального закона распределения длительности пути при вычисленных наиболее вероятном значении и дисперсии можно высказать вероятностные суждения относительно пути. Например:

♦ вероятность того, что критический путь будет больше 3,5 недель, равна 0,1;

♦ вероятность того, что проект можно будет завершить меньше, чем за 50 недель, равна 0,35.

Возможность выдвигать утверждения вероятностного характера относительно длительностей путей в сетевой модели проекта является единственным отличием методов МКП и ПЕРТ. В ПЕРТ'е используются вероятностные оценки длительностей работ, а в МКП - детерминированные. Все остальные вычисления одинаковы.

Последовательность шагов в анализе с учётом неопределённости выглядит следующим образом:

1. Для каждой операции вычисляются ожидаемые значения и дисперсии.

2. Строится сетевая модель проекта, вычисляются времена ранние начала, поздние окончания и резервы для всех операций. Определяется критический путь.

3. Вычисляется дисперсия критического пути как сумма дисперсий критических операций и среднеквадратическое отклонение. На рис. 4.8 показан пример результата расчёта.

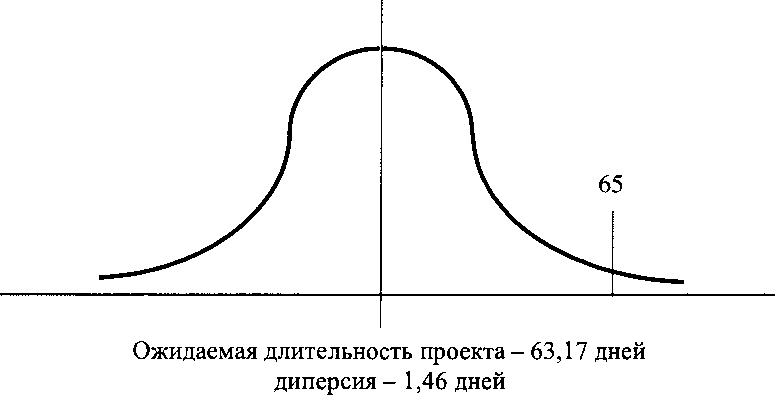
Рис. 4.8

4. Выполняются вероятностные оценки для заданной длительности.

Пусть, например, требуется определить вероятность выполнения проекта за время, не превышающее 65 дней. В теории вероятностей разработан соответствующий математический аппарат. В данном случае можно ограничиться геометрическими соображениями. Вероятность искомого события равна площади под функций распределения слева от длительности в 65 дней. В данном примере вероятность равна 0,894. Следовательно, вероятность того, что проект не уложится в 65 дней, равна 0,106. Исходя из подобных оценок и анализа возможных последствий, окончательно назначается плановая длительность проекта или корректируются сроки в ходе его выполнения.

Стоимостной аспект управления проектами вводится в схему календарного планирования с помощью зависимости «стоимость - время» для каждой операции проекта. На рис. 4.9 показана линейная зависимость, типичная для стоимостных оценок.

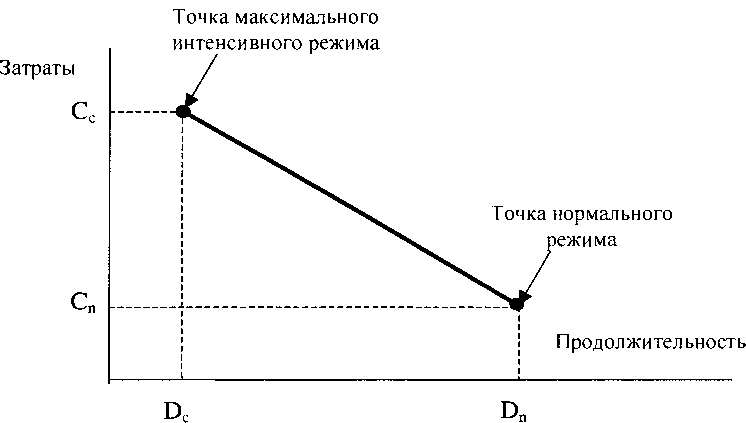
Рис. 4. 9

На рисунке: Б_п- нормальная длительность операции; Б_с- минимальная длительность операции (дальнейшее уменьшение не имеет смысла); С_п,С_с- затраты при нормальной и минимальной длительности операции.

Расчёт с учётом стоимостных факторов направлен на поиск оптимального соотношения «затраты - время» для всего проекта.

В ходе расчёта выполняются следующие шаги:

1. Расчёт сети при нормальном режиме работы для всех операций.

2. Исследование возможностей сокращения длительности проекта. Сокращение длительности возможно только за счёт критических операций. Минимизация роста затрат при этом обеспечивается, если в первую очередь сжимаются работы с меньшими углами наклона графиков «стоимость - время». Ограничением для сжатия служит область действия зависимости «стоимость - время» для рассматриваемой операции.

Шаг 2 повторяется циклически, пока не исчерпываются возможности сжатия сроков проекта. В ходе сжатия могут появляться новые критические пути. Работы, ставшие критическими, включаются в рассмотрение при выявлении очередного претендента на сжатие.

Планы, получаемые в ходе расчёта, фиксируются, а их стоимостные характеристики запоминаются.

3. Выполняется стоимостной анализ, окончательно устанавливается длительность проекта и вариант плана. При этом учитывается, что сжатие первоначального варианта сопровождается ростом прямых затрат и уменьшением косвенных затрат. Прямые затраты участвовали в предыдущих расчётах, а косвенные - нет.

Подход к решению задач на данном шаге иллюстрируется рис. 4.10.

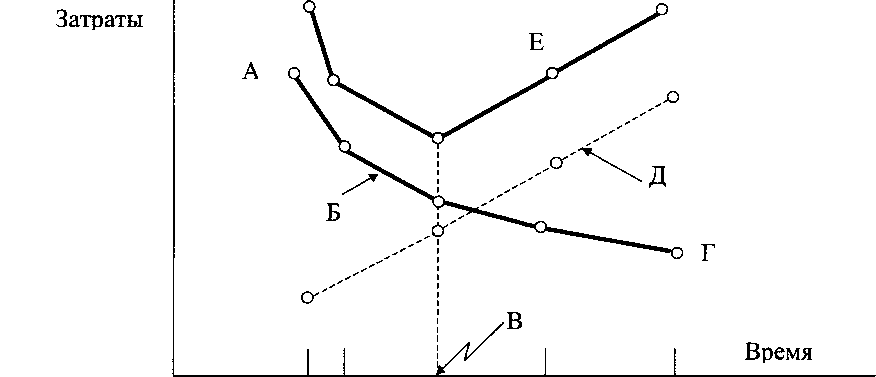
Рис. 4.10

На рис. 4.10 показаны: А - план максимальной интенсивности; Б - прямые затраты; В - план с минимумом затрат; Г - план нормального режима; Д - косвенные затраты; Е - общие затраты.

⇐Сетевая модель проекта | Система управления предприятием типа ERP | Управление процессом реализации проекта⇒