Пусть целевая функция и ограничения нелинейные. Каждый вариант плана характеризуется X, , Х₂, z(x,Х₂). Поиск оптимального решения может быть таким.

Сначала из экономических соображений выделяется область, в которой будут проводиться испытания. На рис. 12 показаны ограничения исходной задачи и область испытаний при случайном поиске.

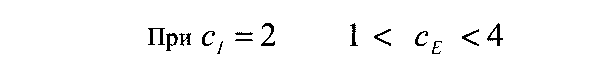
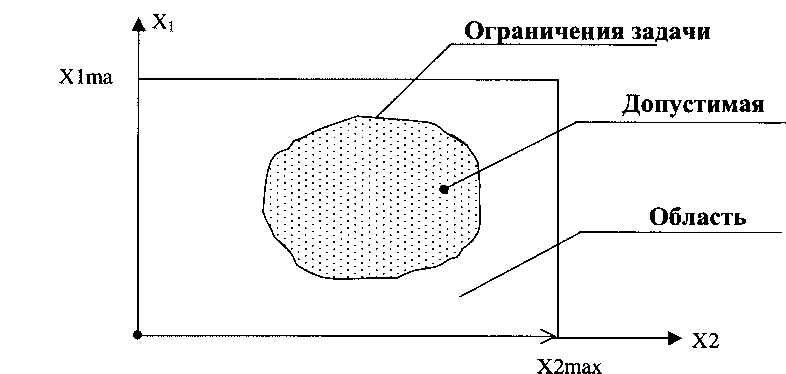
Алгоритм реализуется по шагам:

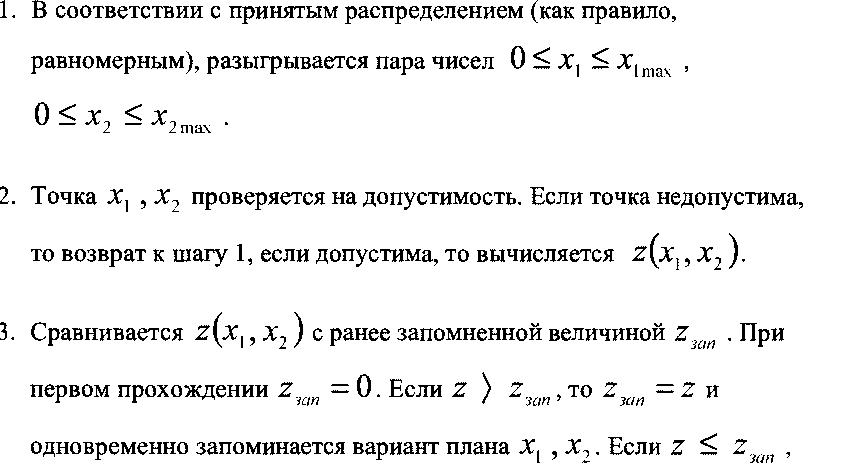
первом прохождении 2_зап= 0. Если 7 ) 2_зап, то 2_зап= г к одновременно запоминается вариант плана X, , Х₂. Если г < 2_зап, то прежний запомненный вариант сохраняется.

4. Выполняется анализ в соответствии с принятым правилом завершения поиска. Если поиск не завершён, то - переход к шагу 1. Если поиск завершён, то - выход из расчёта.

Правила завершения могут быть разнообразными. Приведём в качестве примера два правила:

1. Выполнено заданное число итераций.

2. На заданном числе последних итераций улучшения целевой функции были меньше заданного числа.

⇐Линейное программирование | Система управления предприятием типа ERP | Метод слуайного поиска с локальной оптимизацией⇒