Задача маршрутизации имеет две основные составляющие: сбор информации о состояниях и регулярное ее обновление, а также нахождение выполнимого маршрута на основе имеющейся информации. Качество функционирования любого протокола маршрутизации почти полностью зависит от того, насколько корректно решена первая часть задачи. Заметим, что далее под состоянием будем понимать то, что ранее понималось под базой данных состояний (см. п. 3.2.2 данной главы). Введем некоторые термины.

«Локальное состояние» (local state). Предполагается, что каждый узел имеет свое обновляемое локальное состояние, включающее такие параметры, как задержка распространения, задержка в буфере, доступная остаточная пропускная способность для исходящих линий и, возможно, информация о других ресурсах.

«Глобальное состояние» (global state) является комбинацией локальных состояний всех узлов. Каждый узел способен управлять глобальным состоянием посредством использования либо протокола состояния линии LSP, либо дистанционно-векторного протокола DVP, которые периодически извещают о текущем локальном состоянии соседние узлы (см. выше). Протоколы первого типа широковещательно рассылают информацию о текущем локальном состоянии узла всем остальным узлам сети. Таким образом, каждый узел в сети в определенный момент времени обладает информацией о топологии сети и текущем состоянии всех узлов и каналов. Последнее условие выполняется, естественно, только в случае корректного выбора значения таймера обновления.

Дистанционно-векторные протоколы осуществляют периодический обмен информацией между соседними узлами, как было показано ранее. Для сети, приведенной на рис. 3.4, в табл. 3.3 определено глобальное состояние, т.е. дистанционные вектора для узла Именно эта информация является прототипом для создания таблиц маршрутизации. Глобальные состояния, подобные описанному и хранящиеся на каждом отдельно взятом узле сети, являются аппроксимацией реального текущего состояния вследствие наличия задержки функционирования протокола, распространяющего информацию о локальных состояниях. Чем крупнее сеть, тем грубее аппроксимация.

Глобальное состояние Таблица 3.3

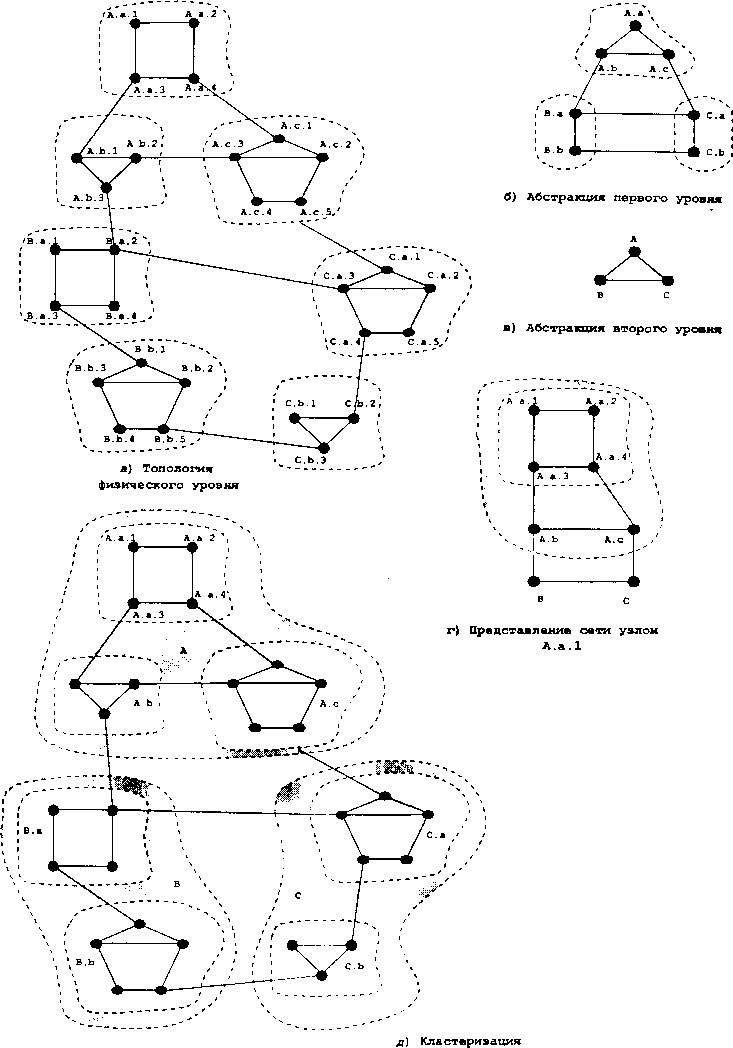
Определение «агрегированного глобального состояния» (aggregated global state) является достаточно распространенным подходом для уменьшения объема информации о глобальном состоянии, это достигается путем логического объединения узлов в соответствии с иерархией сети. На рис. 3.5 представлен подобный подход, рассмотрим его подробнее. На первом этапе, показанном на рис. 3.5.а, производится 9 Зак. 863

кластеризация (логическое объединение), и мы получаем абстрактные группы первого уровня. Узел, имеющий как минимум одну связь с другой группой первого уровня, далее будем назвать пограничным. Далее, в рамках группы выбирается один физический узел, отвечающий за функционирование всей группы, который назначается логическим узлом.

Этот логический узел содержит глобальное состояние полученной в рамках кластеризации логической сети. Линии, соединяющие логические узлы сети, называются логическими. Заметим, что состояние логической линии является комбинацией состояний нескольких линий более низкого уровня иерархии и в этом случае функции протокола состояния линии LSP должны быть расширены, например, как реализовано в сетях ATM в протоколе маршрутизации на интерфейсе «сеть-сеть» или «сеть-узел» (Private Network-Network Interface или Private Network-Node Interface, далее - PNNI) [PNNI].

В зависимости от емкости кластеризуемой сети, возможно дальнейшее логическое разбиение на большие абстрактные группы, соответственно, второго, третьего и т.д. уровней (пример на рис. 3.5.6 и 3.5.в). Приведенный метод кластеризации не является единственным, о других алгоритмах можно прочитать, например, в [Awer98], Отметим, что упомянутый протокол маршрутизации на интерфейсе PNNI построен в соответствии с LSP и его реализация достаточно похожа на протокол OSPF, однако два следующих отличительных факта делают его привлекательным для современных сетей:

• поддержка QoS-маршрутизации;

• возможность применения протокола на различных уровнях сетевой иерархии, что, в отличие от современной сети Интернет, где используются различные протоколы на различных уровнях сетевой иерархии, позволяет добиться достаточно легкой масштабируемости сети.

Каждый физический узел представленной иерархической сети обладает агрегированным глобальным состоянием, в котором хранится различная сетевая информация с разной степенью детализации. В качестве примера на рис. 3.5.г приведено агрегированное глобальное состояние для узла А.а.1. Это состояние строится на основе рекурсивной процедуры, использующей в качестве стартового узел, принадлежащий уровню наивысшей иерархии, и заканчивающей функционирование, соответственно, на самом низком уровне.

Для некоторых задающих качество обслуживания метрик, например, для остаточной пропускной способности, состояние маршрута определяется состоянием линии, у которой пропускная способность, по сравнению с остальными линиями, минимальна. Например, минимальная пропускная способность маршрута s -» i -» j -» t для сети, изображенной на рис. 3.4, равна единице, причем линией, определяющей это значение, является (i, j). В этом случае существует два возможных класса задач:

• оптимизация по пропускной способности линий маршрута (link-optimization), смысл которой заключается в нахождении маршрута с максимальным значением минимальной пропускной способности по всему маршруту. Решение этого класса задач заключается в применении либо модифицированного алгоритма Дийкстра [ D ij к 5 9 ], либо алгоритма Беллмана-Форда [Ford62J;

• удовлетворение требований по параметрам линий маршрута (link-constrained), смысл, которой заключается в нахождении маршрута со значением минимальной пропускной способности, превышающей некоторую заданную величину по всему маршруту. Этот класс задач может быть сведен к первому.

Для остальных метрик, таких как, например, задержка, джиттер задержки, стоимость, состояние маршрута определяется путем объединения состояний линий по всей его протяженности. Например, на рис. 3.4 суммарная задержка в маршруте s -» i -» j -» t составляет 10 единиц. В данном случае также существует два возможных класса задач:

• оптимизация по пропускной способности маршрута (path-optimization), смысл которой заключается в нахождении оптимального, например, по стоимости, маршрута;

• удовлетворение требований по параметрам маршрута (path-cor.strained), смысл которой заключается в нахождении маршрута, в котором значение, например, задержки, находится в требуемых рамках.

Оба представленных класса задач также решаются с использованием алгоритма Дийкстра или Беллмана-Форда. Многие составные, с точки зрения количества метрик, задачи могут быть решены в рамках перечисленных выше четырех основных классов. Например, задача поиска маршрута с удовлетворением требований по полосе пропускания и оптимизации по задержке (bandwidth-constrained, least-delay) может быть решена при помощи объединения классов задач с использованием удовлетворения требований по параметрам линий маршрута и с оптимизацией по пропускной способности маршрута (link-constrained, path-optimization), т.е., фактически, необходимо отыскать маршрут с наименьшей суммарной задержкой и необходимым значением доступной пропускной способности. Таким образом, эта задача сводится к отысканию наикратчайшего, с точки зрения задержки, пути на графе, без учета тех связей, которые не выполняют требований по пропускной способности линий.

В [Nahrstedt98] приведен полный список возможных составных классов задач при маршрутизации unicast. Особый интерес вызывают два класса задач маршрутизации NP-сложности, а именно:

• использующие удовлетворение требований по параметрам маршрута и оптимизацию по пропускной способности маршрута (path-constrained, path-optimization; далее - РСРО), в качестве примера можно привести поиск маршрута с удовлетворением требований по задержке и оптимизации по стоимости (delay-constrained, least-cost);

• использующие удовлетворение множественных требований по параметрам маршрута (multi-path-constrained; далее - МРС), в качестве примера можно привести поиск маршрута с удовлетворением требований по задержке и по джиттеру (delay-j itter-constrai.ned), т.е. нахождение маршрута с заданными пределами значений задержки и джиттера.

Отметим, что для того, чтобы эти задачи обладали NP-сложно^ тью, т.е. чтобы существовало решение, необходимо сделать два предположения:

• метрики независимы;

• их значения могут быть нецелочисленными или целочисленными в заданных пределах.

Если все метрики, за исключением одной, определяются ограниченными целочисленными значениями, или если все метрики зависимы от одной, задача может быть решена в полиномиальном времени с использованием расширенного алгоритма Дийкстра или Беллмана-Ф°Р^да[Chen98]. Добавим, что в работах последних лет, например, [KuiOlb было доказано, что при определенных условиях задача МРС, являющаяся задачей NP-сложности, может быть решена в полиномиальном времени. Кроме того, в работе [КиЮЗ] авторы показали, что задача MPC не обладает NP-сложностью для ряда топологий (графов), в частности, когда узел соединен только с двумя и не более соседними узлами.

⇐Теоретическая модель сети на основе графа | Управление трафиком и качество обслужевания в сети | Обеспечение качества обслуживания при multicast⇒