Классический алгоритм, предложенный в 1986 году J.S. Turner в Turner86], получил невероятное развитие - как будет показано ниже, даже современные «продвинутые» алгоритмы управления и измерения нагрузки используют те же принципы.

Для того, чтобы понять как функционирует данный алгоритм, рассмотрим простой пример. Пусть существует ведро некоторой определенной высоты, в дне которого есть отверстие. В ведро наливается вода, которая выливается через отверстие в дне с определенной постоянной скоростью. Очевидно, что поступающая вода поместится в ведро при условии, что в нем есть место, иначе выльется через край. Таким образом, можно провести аналогию между описанной схемой и буфером, рассматриваемым в непрерывном времени (fluid flow), и именно поэтому алгоритм называется Leaky Bucket («дырявое ведро»).

Существует множество разновидностей алгоритмов Leaky Bucket, далее в этом разделе мы рассмотрим алгоритм, стандартизированный форумом ATM, единственной особенностью которого является фиксированный размер пакета, т.к. он применяется в сетях ATM (пакет - ячейка ATM имеет размер 53 байта).

Одной из главных задач алгоритма Leaky Bucket является измерение и соответствующее управление поступающей нагрузкой, для чего используется счетчик. При поступлении пакета в очередь значение размера счетчика должно быть увеличено на некоторое число, предварительно заданное параметром /, называемым «инкрементом». Если сумма значений размера счетчика и инкремента не превышает размера буфера, то определяется, что поступивший пакет соответствует профилю (является конформным) и помешается в буфер, если же эта сумма превышает размер буфера, то определяется, что поступивший пакет «вне профиля» (не является конформным) и сбрасывается.

Отметим, что в «продвинутых» алгоритмах на основе Leaky Bucket сравнение суммы может осуществляться с некоторым заданным значением, называемым «порог», физически не являющимся максимальным размером буфера. В результате этого пакет, определенный как «вне профиля», может быть не сброшен, а маркирован, например, с более низким, относительно изначального, приоритетом. Значение инкремента I отражает достаточно важный параметр рассматриваемого алгоритма - I определяет время между поступлениями двух последовательных пакетов, т.е. задает интенсивность выходного потока алгоритма Leaky Bucket.

На рис. 2.12 представлена блок-схема рассматриваемого алгоритма. При поступлении первого пакета в Leaky Bucket параметр счетчика нагрузки X устанавливается в ноль, а параметру «время прихода последнего конформного пакета» (Last Conforming Time, далее - LCT) назначается значение времени прихода первого пакета. Размер буфера определяется как сумма переменной L, называемой «предел», и инкремента /. Значение переменной L зависит от максимального размера пачки, которая будет обрабатываться в конкретной реализации. Если предполагается, что через Leaky Bucket будет проходить трафик с высоким значением коэффициента пачечности, то значение L должно быть достаточно высоким (с целью определения конкретных значений ниже будет приведен пример). При поступлении к-го пакета в систему подсчитывается значение переменной X, определяющей разницу между значением счетчика нагрузки X, в момент, когда в систему поступил последний конформный пакет, и временем между поступлением последнего конформного и £-го пакета (рис. 2.12):

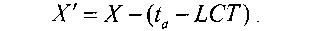
Отметим, что переменная X' может принимать только неотрицательные значения. Если X' больше, чем значение предела L, то поступивший к-й пакет является неконформным, и конформным - в обратном случае. Далее после принятия решения переменные алгоритма должны быть обновлены.

Достаточно важным моментом является также динамика поведения алгоритма. Рассмотрим пример функционирования Leaky Bucket, проиллюстрированный на рис. 2.13. Отметим, что данный пример будет рассматриваться в непрерывном времени (fluid flow). Пусть в дан-

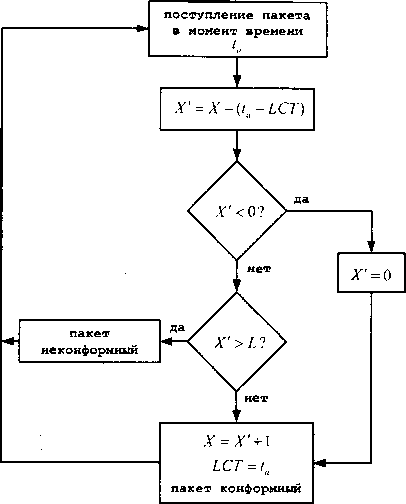
Рис. 2.12. Алгоритм Leaky Bucket, используемый для измерения и управления нагрузкой ном примере значение предела Ь равно шести временным слотам, а значение инкремента I - четырем, т.е. интенсивность обслуживания поступающих в систему пакетов равна одному пакету в четыре временных слота. Таким образом, поступление первого пакета увеличивает счетчик содержимого буфера на четыре единицы.

Далее, второй пакет может поступить в систему только после завершения поступления первого, поэтому, учитывая то, что система рассматривается в непрерывном времени, за один временной интервал, прошедший с момента начала поступления первого пакета до момента начала поступления второго пакета, была обслужена четверть первого пакета. Поэтому в момент поступления второго пакета счетчик содержимого буфера будет иметь значение, равное трем. После поступления второго пакета к значению счетчика прибавляется размер пакета, выраженный во временных слотах, т.е. четыре.

Таким образом, в соответствии с рассмотренным выше алгоритмом, новое значение счетчика не превышает значения (Ь + 1), равного в данном случае десяти, поэтому второй пакет является конформным и переменные алгоритма обновляются, Третий и четвертый пакеты также являются конформными. Рассмотрим поступление пятого пакета. Значение счетчика в момент поступления пятого пакета равно семи - сумма этого значения с размером пакета дает одиннадцать, т.е. превышает значение (L + 1) - пятый пакет неконформный. Значения переменных счетчика и LCT не обновляются.

Далее в данном примере тестой пакет конформен, а пакеты с седьмого по десятый поступают один за другим и формируют пачку, причем, отметим, что перед поступлением седьмого пакета буфер был пустым. Алгоритмом определяется, что три первых пакета из пачки являются конформными, а последний десятый пакет неконформен. Таким образом, для рассматриваемого примера параметр максимального размера пачки MBS должен равняться трем.

Очевидно, что в общем случае для того, чтобы входящий в систему поток являлся конформным, т.е. все пакеты потока были конформными, необходимо выполнение как минимум трех условий - соблюдение параметра MBS (для обеспечения конформности на уровне пачек), обеспечение долговременной средней интенсивности входного потока, равной интенсивности обслуживания в системе, и соблюдение параметра «пиковой скорости» (Peak Rate, далее - PR).

Долговременную среднюю интенсивность входного потока часто называют «устойчивой средней скоростью». (Sustainable Rate, далее - SR) и вычисляют как величину обратную инкременту /. Пиковая скорость определяет значение MBS. Например, если обозначим пиковую скорость через R и возьмем величину Т (между поступлениями двух последовательных пакетов) обратную R, то максимальный размер пачки может быть вычислен следующим образом:

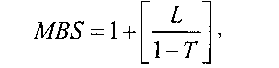
выражение в квадратных скобках округляется в меньшую сторону до целого значения.

Постараемся объяснить эту формулу. Поступление первого пакета увеличивает значение счетчика на /, второго - па (/ -Т) для каждого пакета, приходящего в момент пиковой скорости. Аппроксимируя, можно утверждать, что максимальное количество конформных пакетов может быть примерно Ь/(1-Т)- Для простоты понимания на рис. 2.14 графически представлены определения используемых параметров.

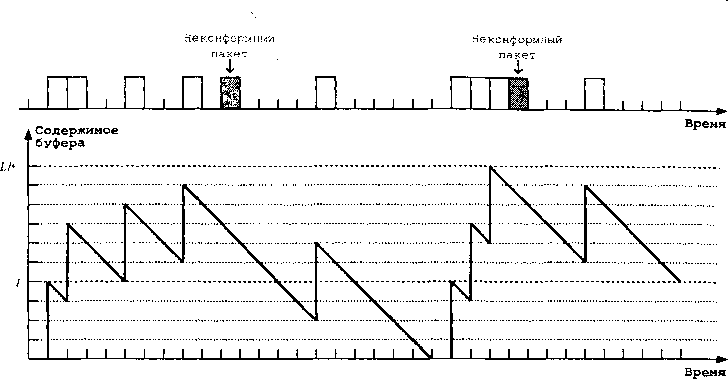
Рис. 2.13. Динамика алгоритма Leaky Bucket

Рис. 2.14. Определения параметров входного потока для Leaky Bucket

Более сложные, относительно рассмотренного только что примера, реализации на основе алгоритма Leaky Bucket обычно используются для контроля за двумя параметрами - устойчивой средней SR и пиковой PR скоростями. Одной из самых распространенных реализаций является «парный Leaky Bucket» (Dual Leaky Bucket), представленный на рис. 2.15. В такой реализации поступающий в систему трафик сначала проверяется первым Leaky Bucket - контролируются значение пиковой скорости PR и значение дисперсии задержки пакета (Cell Delay Variation Tolerance, далее - CDVT), в данном случае - ячейки.

Конформные пакеты направляются во второй Leaky Bucket, в то время как неконформные - сбрасываются или маркируются. Второй по счету Leaky Bucket осуществляет контроль двух других параметров потока конформного с точки зрения PR и CDVT - устойчивой средней скорости SR и максимального размера пачки MBS. Опять же, неконформные этим параметрам пакеты сбрасываются или маркируются, а конформные на выходе Dual Leaky Bucket являются таковыми относительно всех четырех параметров.

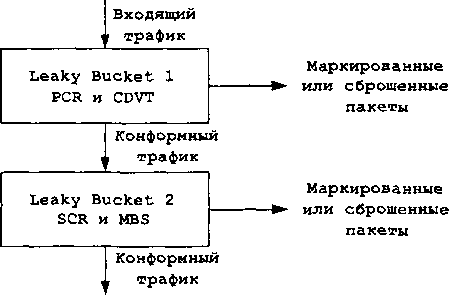
Рис. 2.15. Алгоритм Dual Leaky Bucket контролирует четыре параметра входящего потока

⇐Мониторинг нагрузки | Управление трафиком и качество обслужевания в сети | Алгоритм token bucket⇒