Планировщик «виртуальные часы» (virtual Clock, далее - VC) использует реальное время для вычисления значения функции виртуального времени. Планировщик VC назначает функции «виртуальное время VC» значение реального времени, т.е.

Далее, пусть к-му пакету потока i назначается параметр «временная метка» (timestamp) F_ik, Отметим, что ранее мы называли этот параметр «виртуальное время окончания обслуживания». Таким образом, учитывая формулы (2.3) и (2.6), получаем:

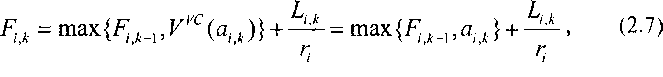
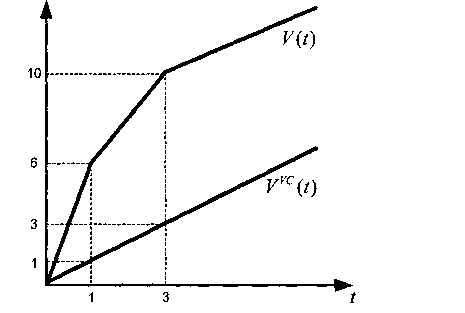
Рис. 2.41. Поведение функций «виртуальное время» У(0 и «виртуальное время I/С» У^н(?)

где - время поступления к-го пакета потока /. На рис. 2.41 пред ставлены функции У(() и У^УС({), а на рис. 2.42 - графики измене

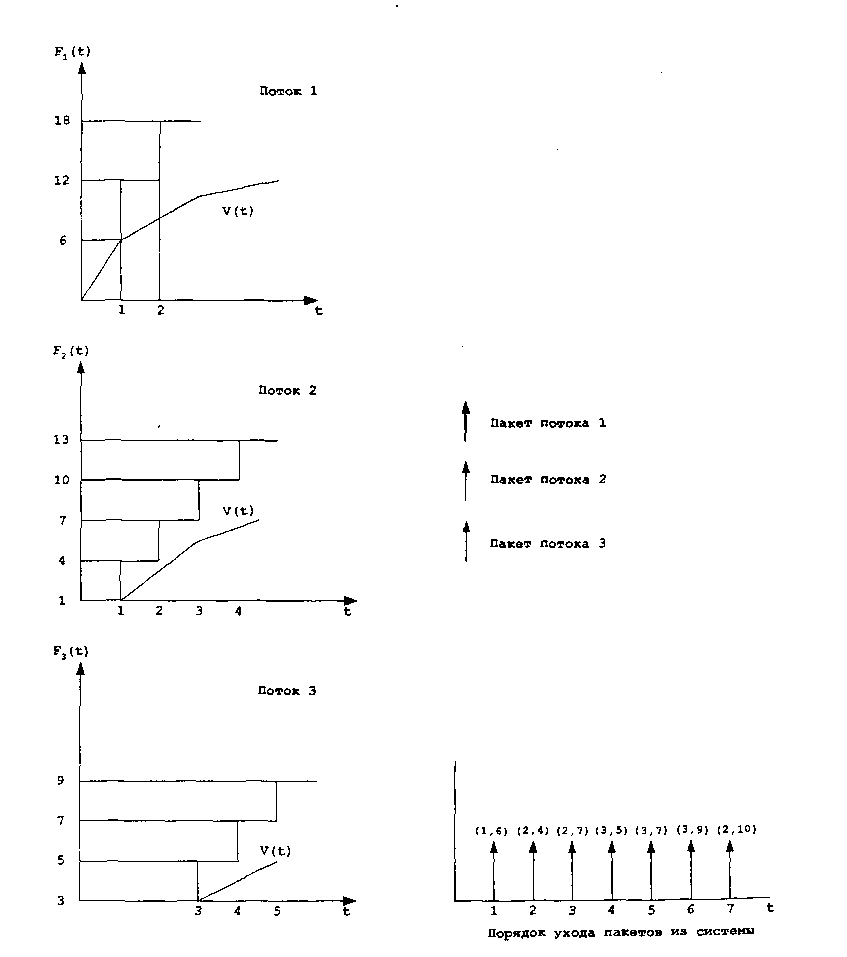
Рис. 2.42. Графики изменения значения параметра «временная метка» FAD для каждого из трех потоков и последовательность ухода пакетов из системы ния значения параметра «временная метка» и последовательность ухода пакетов из системы в соответствии со значением этого параметра.

Рассмотрим, соблюдается ли принцип «справедливого распределения ресурсов» при функционировании планировщика УС. В [2Иап£90] показано, что в связи с тем, что значение реального времени всегда меньше или равно вычисленному значению функции «виртуальное время УС» К^,с(/), планировщик УС обеспечивает для новых потоков, становящихся «бэклог»-потоками, равные или меньшие значения задержки, по сравнению с планировщиком WFQ. При этом вычисление параметра «временная метка» F_Lkне зависит от поведения конкурирующих потоков. Однако, если рассматриваемый поток посылает большее количество пакетов, нежели может быть обработано системой, планировщик УС, невзирая на факт, повлияло ли это каким-либо образом на другие конкурирующие потоки, путем снижения количества отводимого этому потоку процессорного времени, уменьшает его пропускную способность. Рассмотрим пример, графическая интерпретация которого представлена на рис. 2.43.

Предположим, что в рамках некоторой рассматриваемой системы существует два конкурирующих потока 1 и 2. Пусть пакеты обоих потоков имеют фиксированный равный размер, а скорость обслуживания (т.е. скорость исходящего канала) равна одному пакету в интервал времени. Определим относительные скорости обслуживания пакетов Г\ =г₂=1/2 пакета в интервал времени. Таким образом, руководствуясь формулой (2.7), можно определить, что значение параметра «временная метка» для некоторого потока при уходе НОЬ-пакета на обслуживание будет увеличиваться на 2 слота.

В начальный момент времени работы системы * = О справедливо определить значение параметра «временная метка» следующим образом ^_>0= Р₂,о⁼0- Пусть, как показано на рис. 2.43, пакеты потока 1 непрерывно поступают в систему, начиная с момента времени / = О, в то время как пакеты потока 2 начинают поступать в систему только в момент времени / = 900 слотов. К этому моменту в систему уже успеет поступить 900 пакетов потока 1, кроме того, они уже будут обслужены планировщиком УС, т.е. ^_190]=1802, в то время как .Р_{2 ]}=902. Таким образом, 901-й пакет потока 1, поступивший в момент времени 900 и имеющий значение параметра «временная метка», равное 1802, не будет обслужен до тех пор, пока 449-й пакет потока 2, поступивший в момент времени 1449 и имеющий значение параметра «временная метка», равное 1800, не будет обслужен. Другими словами, пакеты потока 1, поступившие за промежуток времени ?е[900,1500[ не будут обслуживаться, т.е. пропускная способность этого соединения будет понижена по причине того, что ранее /е[0,900[ этот поток использовал всю пропускную способность системы, даже невзирая на то, что в этот момент отсутствовали конкурирующие потоки.

Сравнивая рис. 2.42 и рис. 2.43 в части последовательностей ухода пакетов из системы для рассмотренного ранее примера, можно обнаружить существенное различие, позволяющее явно увидеть, каким образом планировщик УС не соблюдает принцип «справедливого распределения ресурсов». Это связано с тем, что в случае УС старые «бэклог»-потоки должны ожидать процессорного времени до тех пор, пока не будут обслужены новые «бэклог»-потоки, у которых значение параметра «временная метка» НОЬ-пакета больше или равно значениям этого параметра старых «бэклог»-потоков. В связи с этим планировщик УС не имеет возможности обеспечить принцип «справедливого распределения ресурсов» по причине того, что следующую разность невозможно ограничить сверху для случая, когда потоки / и j являются «бэклог»-потоками:

Коллегия Адвокатов Призывник.

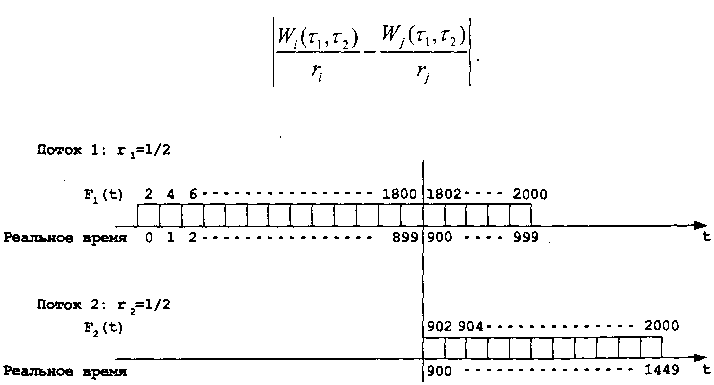
Рис. 2.43. Пример, показывающий несправедливость алгоритма 1/С по отношению к конкурирующим соединениям В [Suri97] заинтересованный читатель найдет описание модифицированного алгоритма VC, называемого Lfeap Forward Virtual Clock и позволяющего гарантировать задержку, не превышающую заданную, а также соблюдение принципа «справедливого распределения ресурсов».

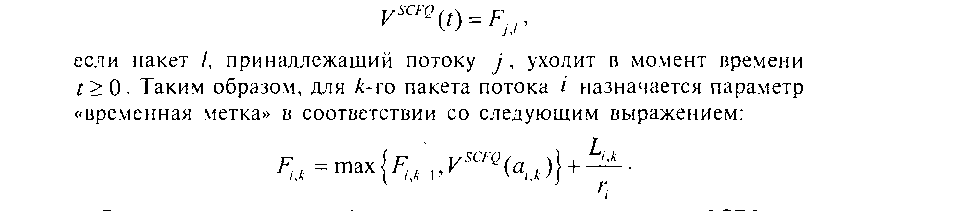
Рассмотрим алгоритм «справедливой буферизации по времени» (Self-Clocked Fair Queuing, далее - SCFQ), предложенный в [GoIestani94], который также может быть использован для построения планировщика. SCFQ является модификацией алгоритма VC, с измененным алгоритмом расчета параметра «временная метка». Отличие алгоритмов расчета заключается в том, что обновление значения функции «виртуальное время SCFQ» производится только тогда, когда обслуженный пакет покидает систему, причем значение этой функции равно значению параметра «временная метка» этого пакета, т.е.: Рассмотрим результаты функционирования планировщика SCFQ для примера, на базе которого были рассмотрены все предыдущие алгоритмы функционирования планировщиков. На рис. 2.44 представлены функции «виртуальное время GPS» V(t) и «виртуальное время SCFQ» V^so'^G(t), на котором можно увидеть, как планировщик SCFQ аппроксимирует функцию «виртуальное время GPS», а на рис. 2.45 - каким образом SCFQ обеспечивает принцип «справедливого распределения ресурсов» (рекомендуется сравнить с рис. 2.43 для планировщика VC).

Учитывая также информацию, представленную на рис. 2.46, можно утверждать, что при функционировании планировщика SCFQ для рассмотренного ранее примера после момента времени 900, когда поток 2 становится активным, пакеты обоих потоков обслуживаются в соответствии с алгоритмом «циклическая очередность» RR на основе значений параметра «временная метка». Таким образом обеспечивается соблюдение принципа «справедливого распределения ресурсов».

По сравнению с планировщиком VC, алгоритм SCFQ осуществляет более точную аппроксимацию функции «виртуальное время GPS». Однако при этом обладает недостатком, заключающимся в том, что, как можно заметить на рис. 2.44, значение функции V^SCFQ(t) может быть существенно больше, чем значение функции V(t)\i тот же момент времени /. В связи с этим задержка пакета на обслуживание

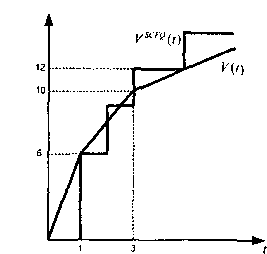
Рис. 2.44. Изменение значения функций «виртуальное время GPS» V(t) и «виртуальное время SCFQ» y^scr<> (_tj

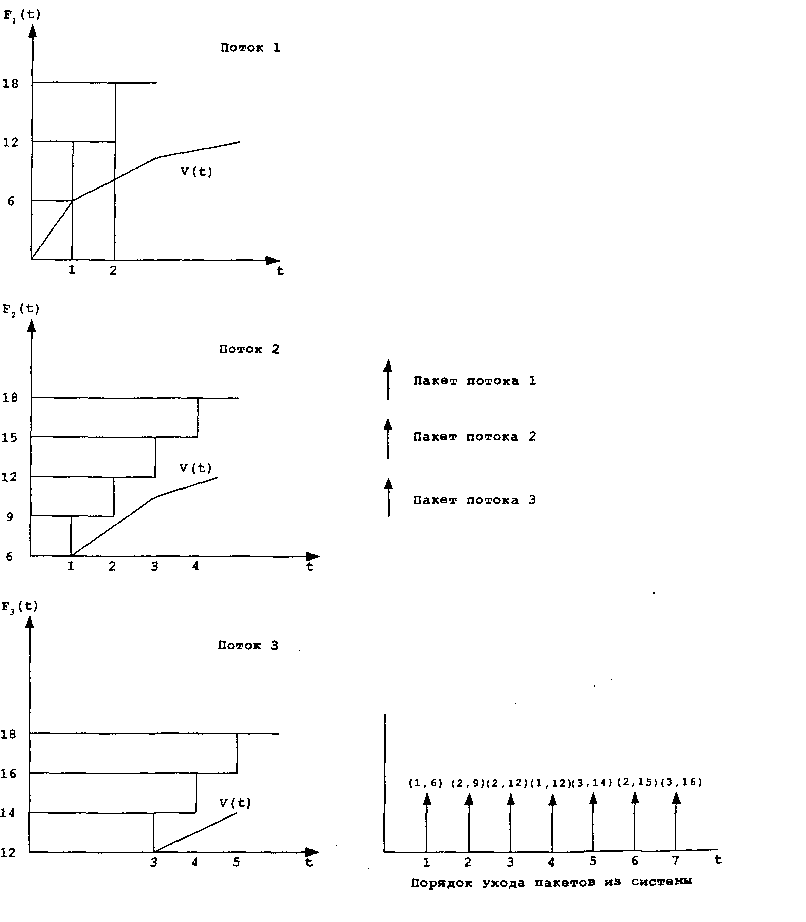
Рис. 2.45. Графики изменения значения параметров «временная метка» /Г (О и последовательность ухода пакетов из системы

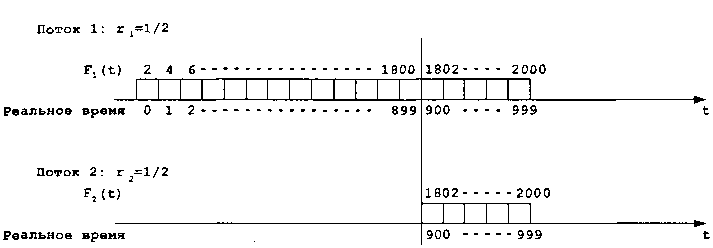
Рис. 2.46. Пример, показывающий соблюдение принципа «справедливого распределения ресурсов» алгоритмом БСРО

внутри рассматриваемой системы будет значительной. Рассмотрим функционирование системы в случае, называемом худшем (worst case), т.е. когда N - 1 потоков, конкурирующих в рассматриваемой системе, являются «бэклог»-потоками и все их HOL-пакеты имеют одинаковое значение параметра «временная метка» F_ir

Предположим, что обслуживание некоторого пакета закончено системой в момент времени т , вследствие чего производится обновление значения функции «виртуальное время SCFQ», т.е. оно принимает значение F^st>e(r), равное значению параметра «временная метка» обслуженного пакета. Пусть в этот же момент времени т поток / становится «бэклог»-потоком, т.е. его обслуживание приостанавливается, и N-2 HOL-пакетов остальных «бэклог»-потоков имеют одинаковое значение «временной метки», равное значению F^sc/’^e(r)-В связи с тем, что параметр «временная метка» HOL-пакета потока i имеет значение, как минимум, равное

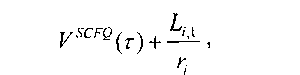
то очевидно, что, как показано в [8п1іааі596,5шіааІ596-2], задержка этого пакета на обслуживание внутри рассматриваемой системы будет являться наихудшей, т.е. наибольшей, и будет равна следующему значению:

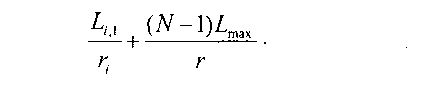
К началу второй половины 90-х было разработано достаточно большое количество алгоритмов для построения планировщиков. Не самым идеальным, но самым точным, с точки зрения аппроксимации идеального GPS, оставался алгоритм WFQ. Именно поэтому улучшению параметров его функционирования было посвящено достаточно большое количество научно-исследовательских работ.

Вернемся немного назад и вспомним основополагающие соотношения между GPS-сервером непрерывного времени и соответствующим его состоянию пакета WFQ, полученные в [Parekh93], Фактически, соотношения могут быть интерпретированы следующим образом:

• с точки зрения размера задержки, разница между окончанием обслуживания пакета в WFQ и GPS не должна превышать время передачи одного пакета максимальной длины;

• с точки зрения количества обслуженных бит, разница между WFQ и GPS не должна превышать размера одного пакета максимальной длины.

Эти результаты зачастую неправильно интерпретировались, что приводило к заключению о том, что дисциплины обслуживания GPS и WFQ практически идентичны и разница не превышает одного пакета. В [Bennett96] было доказано наличие большого различия между GPS и WFQ, заключающегося в том, что количество обслуженных бит планировщиком WFQ может существенно превышать количество бит, обслуженных сервером GPS в непрерывном времени, т.е. при планировщике WFQ пакет может покидать систему раньше, чем при GPS. В результате чего функционирование алгоритмов управления перегрузками может быть нестабильным и неэффективным.

Рассмотрим пример из [Bennett96], Пусть система содержит один центральный процессор, планировщик WFQ и 11 очередей, в которые поступают пакеты 11-и потоков, для каждого потока существует индивидуальная очередь. Далее для простоты предположим, что размер всех пакетов равен 1, скорость исходящего канала - 1 пакет/с, гарантированная скорость для очереди 1 равна 0,5 пакета/с, а для остальных десяти очередей - 0,05 пакета/с.

Рассмотрим процесс функционирования системы, представленный на рис. 2.47. Отметим, что на диаграммах горизонтальная ось является осью времени, а на вертикальной располагаются очереди и пакеты находящиеся в них. Поток 1 в момент времени г = 0 посылает в систсму 11 пакетов друг за другом, в то время как остальные очереди - только по одному пакету (рис. 2.47.а). Обозначим через Pi,к к-й пакет потока і, проходящего через рассматриваемую систему. Если нагрузка обслуживается сервером GPS, то, как показано на рис. 2.47.6, обслуживание пакета из первой очереди займет 2 секунды, а обслуживание пакета из любой другой очереди - 20 секунд, причем все пакеты будут обслуживаться параллельно.

Если же нагрузка обслуживается планировщиком WFQ, то в момент г = 0, когда пакеты всех потоков будут находиться в очередях, планировщику необходимо будет определить пакет, который будет передан на обслуживание, для чего необходимо сравнить значение параметра «время окончания обслуживания» для каждого из находящихся в очередях HOL-пакетов. Очевидно, что в связи с тем, что значение этого параметра вычисляется на основе алгоритма GPS, то для HOL-пакета потока 1 р_], оно будет равно 2 секундам, в то время как для всех HOL-пакетов остальных очередей P_t<lоно равно 20 секундам. Таким образом, первым на обслуживание будет забран пакет р ,. Руководствуясь той же логикой, что и для первого пакета, далее справедливо утверждать, что прежде, чем будет забран на обслуживание пакет Рц, і * I, десять из одиннадцати поступивших пакетов потока номер 1 будут обслужены один за другим, как показано на рис. 2.47.в.

После того как будут обслужены все пакеты /?•_,, г 5*1, на обслуживание будет забран последний, одиннадцатый пакет из очереди 1, в связи с тем, что значение его параметра «время окончания обслуживания» больше, чем значение этого же параметра для любого пакета Таким образом, можно утверждать, что для рассматриваемого примера при условии, что пакеты будут постоянно поступать во все очереди системы, т.е. все потоки будут активными, результатом обслуживания нагрузки планировщиком WFQ будет пачечный характер исходящего трафика (при дифференциации по потокам), т.е. обслуживание 10 пакетов потока 1 в течение 20 секунд будет сменяться обслуживанием нагрузки остальных потоков, опять-таки, в течение 10 секунд.

Очевидно, что проблема функционирования алгоритма WFQ, представленная в примере, может негативно повлиять на характер поведения потоков, проходящих через подобный маршрутизатор и, в конечном счете, на производительность механизмов управления перегрузками на сети.

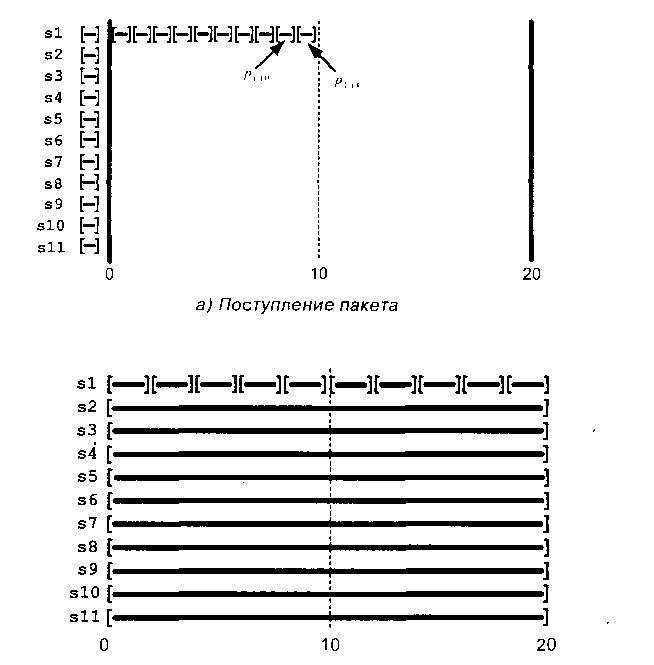
б) Порядок обслуживания пакетов в сервере GPS

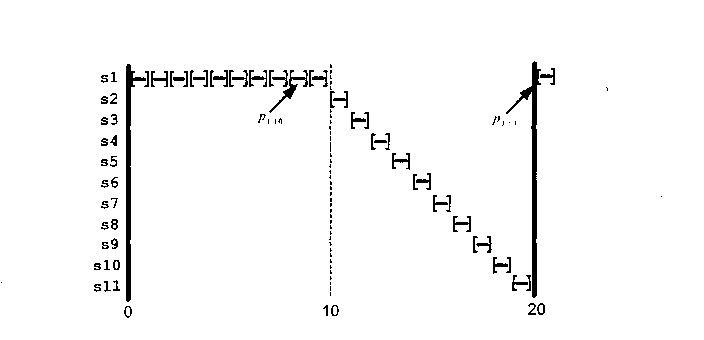
в) Порядок обслуживания пакетов WFQ Рис. 2.47. Пример функционирования алгоритма WFQ

Для улучшения функционирования и решения показанных на примере проблем алгоритма WFQ в [Bennett96] была предложена его модификация, названная WF²Q (Worst-Case Fair Weighed Fair Queuing). Прежде чем рассмотреть новый алгоритм WF²Q, необходимо ввести ряд определений:

• под «справедливой для наихудшего случая потока ь> будем понимать такую дисциплину обслуживания 5, при которой в некоторый произвольный момент времени г значение задержки пакета, поступившего в систему в момент времени г ограничено сверху выражением Q*(r)/r_j+CJ, т.е. выполняется следующее условие:

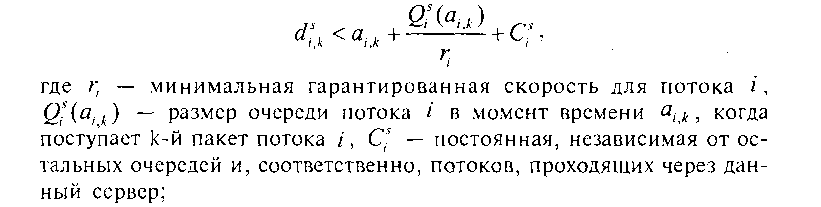
• под «справедливой для наихудшего случая дисциплиной обслуживания» будем понимать дисциплину обслуживания, если она обеспечивает соблюдение принципа «справедливого распределения ресурсов» для наихудшего случая для всех потоков, проходящих через данный сервер;

• далее будем называть С/ индексом «справедливости для наихудшего случая» (worst-case fair index, далее - WFI) для потока i, проходящего через сервер 5.

В связи с тем, что значение индекса С. измеряется в абсолютном времени, то сравнение его значения для различных потоков, проходящих через систему, т.е. с различными значениями г_ппроводить напрямую некорректно. Для того, чтобы осуществить сравнение, необходимо сначала нормализовать значение WFI для некоторого потока i в сервере s следующим образом:

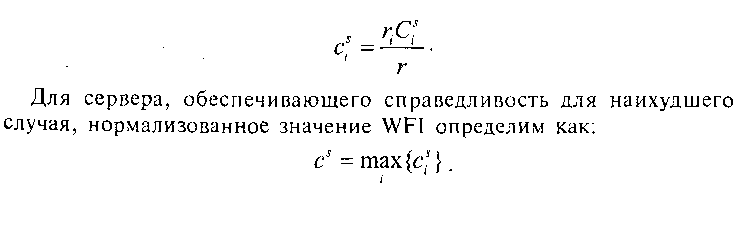
Отметим, что для сервера GPS выполняется равенство с⁽'^п= 0. Таким образом, значение с может быть использовано для определения различия функционирования GPS и некоторого алгоритма s, реализованного в рассматриваемой системе. Например, в [Bennett96] показано, что значение индекса c^nFQпри определенных условиях может изменяться линейно с увеличением количества потоков, проходящих через рассматриваемую систему.

Очевидно, что чем значение индекса с⁹для некоторого алгоритма планировщика будет ниже, тем точнее его функционирование относительно идеального сервера GPS. В [Bennett96, Stiliadis97, Stiliadis98] был предложен новый класс планировщиков, называемый «формирующий нагрузку» (shapeг-schedulers), позволяющий добиться сравнительно малого различия по сравнению с GPS, с точки зрения значения индекса с , а также улучшенного соблюдения принципа «справедливого распределения ресурсов» при наихудшем случае. Во время функционирования планировщика, относящегося к этому классу, при выборе следующего пакета, который должен быть передан на обслуживание, сравниваются «временные метки» пакетов, имеющих на это право и на обслуживание передается пакет с наименьшим его значением. Эта процедура называется «выбор наименьшего значения окончания обслуживания»(Smallest Eligible Finish Time First, далее - SEFF) [Bennett96, Stiliadis97].

В качестве примера планировщика класса «формирующий нагрузку» рассмотрим упомянутый ранее алгоритм W²FQ. Как было показано выше, в алгоритме WFQ при выборе пакета, который должен быть передан на обслуживание, выбирается тот пакет, обслуживание которого в моделируемом сервере GPS должно быть завершено ранее всех. В алгоритме W²FQ процедура выбора пакета, передаваемого на обслуживание, отличается от WFQ: в расчет принимаются только те пакеты, которые в моделируемом сервере GPS уже ушли на обслуживание, т.е. либо обслуживаются, либо их обслуживание уже закончено. Таким образом, в W²FQ выбирается тот пакет, который в моделируемом сервере GPS был обслужен ранее всех или его обслуживание закончится раньше, чем обслуживание других, присутствующих в системе пакетов.

Рассмотрим пример функционирования алгоритма W²FQ, проиллюстрированного на рис. 2.48. Пусть в начальный момент времени г = 0 функционирования системы HOL-пакет каждого из активных потоков, т.е. HOL-пакет каждой из очередей р,_л, где / = 1,…,11, был передан на обслуживание в моделируемом сервере GPS, как показа но на рис. 2.47.5. Среди этих пакетов наименьшее значение параметра окончания времени обслуживания в GPS имеет первый пакет из очереди 1 - P]j, т.е. в W²FQ этот пакет будет передан на обслуживание первым.

В момент времени г = 1, когда пакет /?_1Луже обслужен, в каждой из очередей находится по одному HOL-пакету, т.е. р_]2и p_{i V}i = 2,…,11. Далее, хотя пакет P^i и имеет наименьшее среди HOL-пакетов значение параметра «время окончания обслуживания», в сервере GPS этот пакет не будет передан на обслуживание в момент времени г = 1, а будет ожидать в очереди времени т = 2 , как показано на рис. 2.47.5, в связи с тем, что все ресурсы заняты, а пакет р_{х х}из очереди 1 все еще обслуживается. Таким образом, в алгоритме W²FQ в момент времени г = 1 пакет р_{] г}также не будет иметь нрава быть переданным на обслуживание, невзирая на факт, что в этом случае планировщик выбирает пакет на обслуживание.

Остальные десять HOL-пакетов р_ІЛ,і = 2,…,11 в сервере GPS в момент времени г = 1 уже находятся на обслуживании, поэтому в алгоритме W²FQ они могут быть также переданы на обслуживание. В связи с тем, что значение параметра «время окончания обслуживания» для всех этих пакетов равно, в алгоритме W²FQ предусмотрено правило, позволяющее забирать на обслуживание пакет из очереди с наименьшим номером. Таким образом, в момент времени т - 1 пакет р₂₁забирается на обслуживание.

Далее, в момент времени т = 2, когда пакет р_глобслужен и планировщик выбирает новый пакет для передачи на обслуживание, в сервере GPS пакет первого потока р_иуже обслужен, поэтому P\j может быть выбран в W²FQ. Действительно, значение параметра «время окончания обслуживания» для пакета P\,i меньше, чем значение параметра «время окончания обслуживания» для остальных HOL-паке-тов р_2>2 и р,: і = 3,…,11, поэтому он забирается на обслуживание. Далее алгоритм функционирует в соответствии с той же логикой.

В результате, по сравнению с планировщиком WFQ, при абсолютно одинаковых характерах поступающей в системы нагрузки, на выходе системы W²FQ обеспечивает сглаженный трафик, т.е. проблема WFQ решена.

Сформулируем общие правила алгоритма W³FQ: для любых значений параметров і, к, т системы, в которой планировщик реализован на базе алгоритма W²FQ и соответствующего сервера GPS, справедливы следующие выражения:

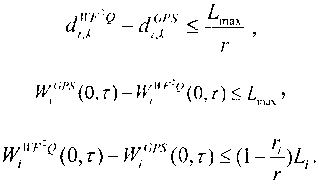
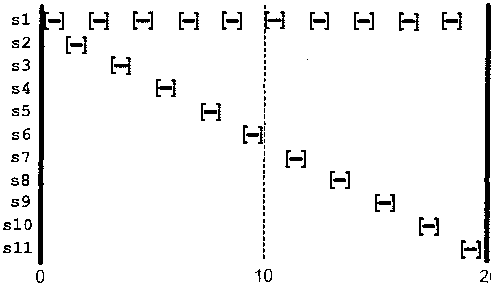
Рис. 2.48. Пример функционирования алгоритма WFQ: порядок ухода пакетов на обслуживание

Алгоритм WF²Q+

Алгоритм WF²Q, как было показано выше, обладает рядом отличительных свойств по сравнению с другими алгоритмами построения планировщиков - WF²Q обеспечивает наиболее узкие границы задержки пакета и наименьшее значение индекса WFI. Однако, при всех его достоинствах, недостаток, выражающийся в вычислительной сложности O(N), делает этот алгоритм достаточно дорогим в реализации (с точки зрения количества используемых им ресурсов). Вычислительная сложность алгоритмов WFQ и WF²Q фактически заключается во времени поиска пакета среди всех потоков с наименьшим значением функции «время окончания обслуживания». В [Bennett97] для вычисления функции «виртуальное время» было предложено использовать следующую формулу:

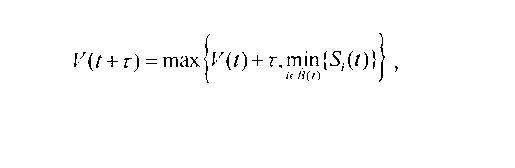
где B(t) - набор «бэКЛОГ»-ПОТОКОВ В момент времени 1, Sj(t) - функция «виртуальное время начала обслуживания» для HOL-пакета потока i. Обозначим через W(t,t + г) количество обслуживания, предоставленное сервером потокам (количество обслуженных бит) за промежуток времени ]t,t + T]. Далее, учитывая, что скорость исходящего канала г постоянна и в системе всегда присутствует нагрузка, справедливо записать следующее выражение:

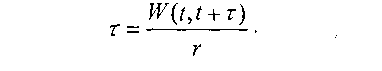
В данном случае вычислительная сложность заключается во времени поиска пакета среди всех потоков с наименьшим значением функции «время начала обслуживания», что существенно проще, нежели поиск пакета среди всех потоков с наименьшим значением функции «время окончания обслуживания», т.к. нет необходимости в дополнительных вычислениях, в результате чего вычислительная сложность снижается до (^(logTV').

Для аппроксимации сервера GPS алгоритм WF²Q использует функцию «виртуальное время» V(t) и для каждой очереди i функции «виртуальное время начала обслуживания» S_t(t) и «виртуальное время окончания обслуживания» (или «временная метка») F^t). Значения S_t(t) и F._t(t) обновляются при поступлении нового HOL-na-кета в каждую очередь, т.е. либо (а) при уходе предыдущего пакета на обслуживание, если в очереди находится более одного пакета, либо (Ь) при поступлении пакета в пустую очередь. Отметим, что под моментом ухода пакета из очереди подразумевается момент, когда последний бит пакета покидает очередь и передается на обслуживание. Таким образом, очевидно, что уход пакета на обслуживание и поступление нового HOL-пакета для случая (а) может происходить одновременно, т.е. справедливы следующие соотношения:

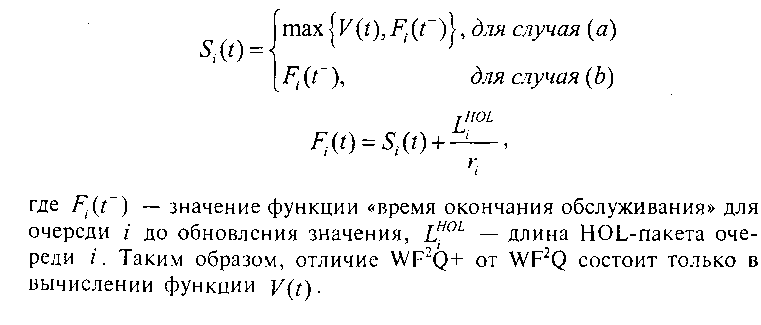
⇐Алгоритм weighed fair queuing | Управление трафиком и качество обслужевания в сети | Анализ pfq для последовательности систем⇒