Важным свойством всех алгоритмов планировщиков семейства PFQ является возможность обеспечения гарантий по задержке пакета «из-конца-в-конец» для наихудшего, с точки зрения нагрузки, случая при совместном функционировании с Leaky Bucket, используемым для контроля за поступающим в систему трафиком. Рассмотрим пример, иллюстрирующий вышесказанное. Предположим, что существует система, в которую поступает трафик п потоков. Пусть на входе в очередь трафик каждого потока регулируется индивидуальным Leaky Bucket с параметрами (о^-,.,/?,.), где i - номер потока, сг. - значение максимальной пачечности, a p_t- средняя интенсивность потока. Для этого случая в [Parekh93] доказано, что количество информации потока г, поступившей за интервал времени ]*V], может быть определено следующим образом:

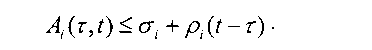
Рассмотрим далее функционирование планировщиков PFQ в сетевом окружении, т.е. предположим, что существует последовательность систем в количестве К (напомним, что под системой понимается модель маршрутизатора), через которые проходит некоторый поток i. Пусть в каждой системе реализован планировщик. Предположим, что скорость каждого исходящего, по отношению к системе, канала равна г и планировщик в рамках каждой системы предоставляет потоку i гарантированную полосу пропускания, т.е. Обозначим че рез L_tи L_maxмаксимально разрешенный размер пакета для потока i и максимально разрешенный размер пакета на всей рассматриваемой сети, соответственно. Значение задержки пакета «из-конца-в-конец» для наихудшего, с точки зрения нагрузки, случая вне зависимости от поведения остальных потоков на всей сети для некоторого потока i не будет превышать следующего значения (не учитывая задержку распространения сигнала):

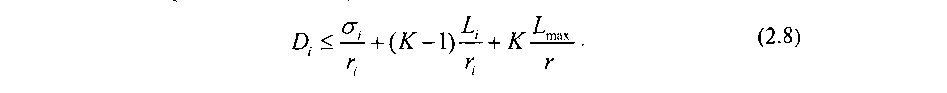
На рис. 2.49 показано каким образом вычисляется задержка пакета «из-конца-в-конец» для случая прохождения пакета через последовательность систем в соответствии с формулой (2.8). Обозначим через с!_к,к = 1,…,К систему в рассматриваемой последовательности. На рис. 2.49.Д представлен случай для пакета потока /, проходящего через первую в последовательности систему или, с другой точки зрения, если система является единственной, т.е. К ■= 1. Для этого случая задержка пакета, проходящего через эту систему, равна:

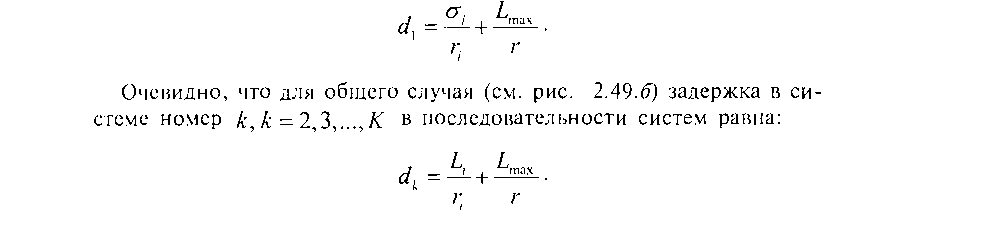
Таким образом, получаем, что £). =d_x+(К-\)d_k, т.е. имеем неравенство (2.8). Интуитивно это неравенство можно объяснить следующим образом. Первая составляющая: несмотря на то, что поток i проходит через последовательность систем, ситуацию можно рассмотреть как будто бы этот поток проходит через одну систему, планировщик которой предоставляет этому потоку гарантированную полосу пропускания Поэтому, если рассматриваемый поток / имеет длину пачки, равную сг., то значение задержки пакета для наихудшего, с точки зрения нагрузки, случая равно отношению arjf) , что эквивалентно, если бы пример рассматривался в непрерывном времени с планировщиком GPS.

\

Вторая составляющая неравенства отражает возможную задержку в каждой из систем в последовательности в случае, когда вновь по-

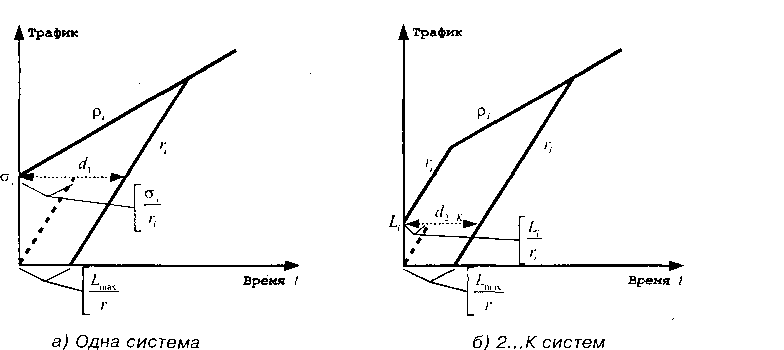
Рис. 2.49. Вычисление задержки пакета «из-конца-в-конец» для случая прохождения пакета через последовательность систем ступивший пакет потока i должен ожидать в очереди, пока предыдущий пакет, принадлежащий этому же потоку, не будет обслужен, т.е. максимальная задержка на этом этапе не превысит значения Ljr . Третья составляющая неравенства отражает возможную задержку в каждой из систем в последовательности в случае, когда вновь поступивший пакет потока i должен ожидать в очереди, пока обслуживаемый в момент поступления пакет другого потока не будет обслужен, т.е. максимальная задержка на этом этапе не превысит значения Ашх/^Г■ Неравенство (2.8) может быть преобразовано и для различных случаев, например, для гетерогенной сети, где скорости исходящих каналов различны [Georgiadis96.

В [Parekh93j и [Parekh94] была доказана теорема, показывающая, что при правильном выборе параметров для некоторого потока /, проходящего через последовательность систем с реализованными идентичными планировщиками WFQ, возможно обеспечение ограниченного сверху значения задержки пакета «из-конца-в-конец» для наихудшего, с точки зрения нагрузки, случая. Также доказано, что параметрами, значения которых необходимо правильно выбрать, являются только лишь значения т_гТаким образом, рассмотренный пример является доказательством того, что услуга гарантированной доставки информации через сеть Best Effort может быть реализована лишь только при помощи выделения рассматриваемому потоку определенной полосы пропускания. Именно эта стратегия была использована в архитектуре Интегральных Услуг IntServ при помощи протокола резервирования полосы пропускания RSVP - приемник имеет возможность выбора размера полосы пропускания для потока с целью обеспечения требуемой задержки.

В [Keshav97, Zhang95] для общего случая доказаны следующие выражения для вычисления максимального гарантированного значения задержки D при прохождении пакета некоторого потока через к, к = 1,2,…,К узлов для различных алгоритмов планировщиков (без учета фиксированных задержек):

• для планировщика GPS:

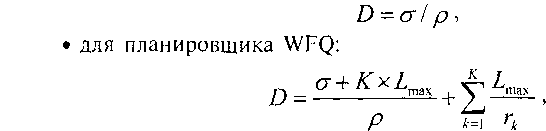
где N_k- число конкурирующих потоков в к-м узле (планировщике), г_к- скорость исходящего канала узла.

⇐Алгоритм virtual clock | Управление трафиком и качество обслужевания в сети | Сравнение и анализ алгоритмов планировщиков⇒