Целью разработки данного принципа маршрутизации является решение проблемы масштабируемости для маршрутизации от источника. Как результат, иерархическая маршрутизация является хорошо масштабируемой по причине объединения групп физических узлов в логические узлы и, как следствие, уменьшения громоздкости глобальных состояний. При иерархической маршрутизации для нахождения выполнимого маршрута могут применяться алгоритмы маршрутиза ции от источника, которые используют в качестве исходных данных агрегированные состояния. Однако, при иерархической маршрутизации, по сравнению с другими, повышается вероятность того, что используемые агрегированные глобальные состояния являются недостаточно точной аппроксимацией реального текущего состояния сети. Очевидно, что это негативно влияет на качество обслуживания. В качестве примера можно рассмотреть абстрактную картину сети, т.е. построенную на базе агрегированного глобального состояния, с точки зрения узла А.а.1, приведенную на рис. 3.5.г.

В данном случае практически невозможно оценить задержку «из-конца-в-конец» для гипотетического соединения «узел А.а.1 - узел абстрактной группы С» по причине того, что структура абстрактной группы С узлу А. а. 1 неизвестна. Более того, например, внутри абстрактных групп А. с и С параметры линий могут постоянно меняться. С точки зрения агрегированного глобального состояния, маршрут для нашего гипотетического соединения будет проходить от группы А. а всего через две абстрактные линии со своими параметрами, которые являются аппроксимацией текущего состояния физических линий внутри абстрактных групп. Подобные неточности неизбежны при иерархической маршрутизации.

В случае, если качество обслуживания обеспечивается с удовлетворением по значениям нескольких метрик, задача иерархической маршрутизации становится еще более сложной. Рассмотрим пример, представленный на рис. 3.7. Пусть имеется два требования по значениям метрик - это полоса пропускания и задержка. Четыре узла, которые обозначим 0.1, 0.2, 0.3и0.4, объединим в абстрактную группу о. Будем считать, что вследствие агрегирования параметры пропускной способности и задержки физических линий внутри группы 0 будут отражены в новых значениях параметров линий (о, Е), которые и необходимо определить.

Очевидно, что руководствуясь заданными метриками качества обслуживания, необходимо найти маршрут от о. 1 к о. 2 с максимальным значением параметра пропускной способности.и минимальной задержкой. При выполнении требований по первой метрике искомым является маршрут Р1 = 0.1 -> 0.3 -> 0.4 -> 0.2 со значением пропускной способности, равным 3. Далее находя минимальное значение из двух, характеризующих маршрут 0.1 -> о. 2 и линию (о. 2, г), определяем, что значение пропускной способности для абстрактной линии (о, г) равно 3. Для удовлетворения требования по второй метрике, задержке, выполним подобную процедуру. В результате определим маршрут с наименьшим значением задержки Р2 = 0.1 -> э.2 со значением, равным 1. Таким образом, значение задержки абстрактной линии (о, г) равно двум, т.е. сумме задержки внутри абстрактной группы о (маршрута Р2) и задержки линии (с. 2, г). Описанный подход к решению задачи маршрутизации с выполнением требований по нескольким метрикам является некорректным по причине того, что найденные маршруты Р1 и Р2 не совпадают.

Сеть, на примере которой рассмотрена задача, является примитивной и, как следствие, на реально функционирующих сетях задача иерархической маршрутизации с удовлетворением по значениям нескольких метрик может быть чрезвычайно сложной. На данный момент проблема стыковки различных метрик при решении задачи (}о5-маршругизации является открытой.

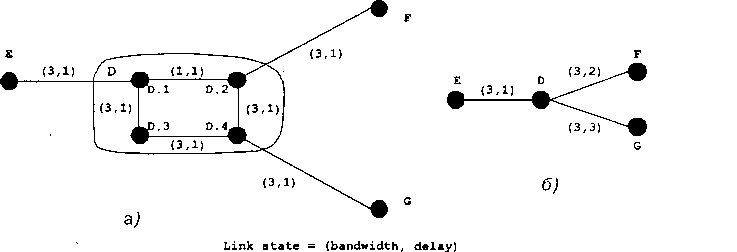
Рис. 3.7. а) структура абстрактной группы О; б) некорректное вычисление параметров абстрактной линии (Э, Р)

⇐Распределенная маршрутизация | Управление трафиком и качество обслужевания в сети | Оптимизация параметров алгоритма функционирования протокола маршрутизации типа lsp⇒