Информационный фонд системы управления должен обеспечивать получение выходных наборов данных из входных с помощью алгоритмов обработки и корректировки данных. Это возможно, если создана инфологическая модель предметной области, которая вместе с наборами хранимых данных и алгоритмами их обработки позволяет построить каноническую модель (схему) информационной базы, а затем перейти к логической схеме и далее - к физическому уровню реализации.

Инфологической (концептуальной) моделью предметной области называют описание предметной области без ориентации на используемые в дальнейшем программные и технические средства. Однако для построения информационной базы инфологической модели недостаточно. Необходимо провести анализ информационных потоков в системе в целях установления связи между элементами данных, их группировки в наборы входных, промежуточных и выходных элементов данных, исключения избыточных связей и элементов данных. Получаемая в результате такого анализа безызбыточная структура носит название канонической структуры информационной базы и является одной из форм представления инфологической модели предметной области.

Для анализа информационных потоков в управляемой системе исходными являются данные о парных взаимосвязях, или отношениях (т.е. есть отношение или нет отношения), между наборами информационных элементов. Под информационными элементами понимают различные типы входных, промежуточных и выходных данных, которые составляют наборы входных N\, промежуточных Л'2 и выходных А'з элементов данных.

Формализованно связи (парные отношения) между наборами информационных элементов отображаются в виде матрицы смежности В, под которой понимают квадратную бинарную матрицу, проиндексированную по обеим осям множеством информационных элементов D = fd\, d.2,-,d_s}, где .? - число этих элементов:

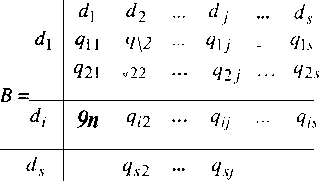
В позиции (/, ]) матрицы смежности записывают 1 (т.е. = 1), если между информационными элементами Л/ и ^ существует отношение Ло, такое, что для получения значения информационного элемента необходимо непосредственное обращение к элементу с1]. Наличие такого отношения между о',- и ^ обозначают в виде ф Яо $, чему соответствует =1, а отсутствие - в виде ф /?о ^, т.е. ду = 0. Для простоты принимают, что каждый информационный элемент недостижим из самого себя:

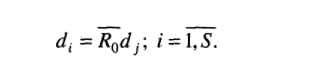
Матрице В ставится в соответствие информационный граф О - (Б, Яо). Множеством вершин графа О - (А /?о) является множество Б информационных элементов, а каждая дуга (ф, <г//) соответствует условию 4' До Ф, т.е. записи 1 в позиции (г/) матрицы В.

Например, задано множество Б из четырех наборов информационных элементов, т.е. Б = (й\ й2, ёц}. Пусть матрица смежности В этих элементов имеет вид:

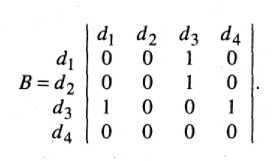
Из этой матрицы видно, что для вычисления элемента необходимо обращение к элементам ё\ и ^ а для получения элемента с?4 - к элементу ^з. Чтобы получить элемент ё\, надо обратиться к й?з. Элемент ^2 не зависит от других элементов матрицы. Информационный граф в этом простейшем случае будет соответствовать рис. 5.1.

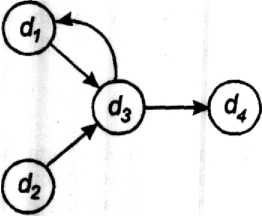
Рис. 5.1. Информационный граф О = (ДЛо)

В общем случае структура графа О = (О,Ко) вследствие неупорядоченности сложна для восприятия и анализа. Составлейная на основе инфологической модели, она не гарантирована от неточностей, ошибок, избыточности и транзитивности. Для формального выделения входных, промежуточных и выходных наборов информационных элементов, определения последовательности операций их обработки, анализа и уточнения взаимосвязей на основе графа О = (А/? о ] строят матрицу достижимости.

Матрицей достижимости М называют квадратную бинарную матрицу, проиндексированную по обеим осям множеством информационных элементов Б аналогично матрице смежности В. Запись 1 в каждой позиции (у) матрицы достижимости соответствует наличию для упорядоченной пары информационных элементов (с1], $]) смыслового отношения достижимости Я. Элемент ^ достижим из элемента ] т.е. выполняется условие $ Я₀$], если на графе О - (Д/?о) существует направленный путь от вершины с/_г- к вершине <1] (в процессе получения значения элемента с/у используется значение элемента ё]). Если фЯ₀] то отношение достижимости между элементами $ и с/, отсутствует и в позиции (у) матрицы М записывают 0. Отношение достижимости транзитивно, т.е. если $]Яос1к и йк Я О $], то ф'Яой/, I, ], к = 1, 5.

Записи 1 в/-м столбце матрицы М соответствуют информационным элементам ф, которые необходимы для получения значений элементов с?,- и образуют множество элементов предшествования А(ф) для этого элемента. Записи 1 в /-Й строке матрицы М соответствуют всем элементам <// , достижимым из рассматриваемо мого элемента ф и образующим множество достижимости ЯЩ) этого элемента. Информационные элементы, строки которых в матрице М не содержат единиц (нулевые строки), являются выходными информационными элементами, а информационные элементы, соответствующие нулевым столбцам матрицы М, являются входными. Это условие может служить проверкой правильности заполнения матриц В и М , если наборы входных и выходных информационных элементов известны. Информационные элементы, не имеющие нулевой строки или столбца, являются промежуточными.

Для полученного графа (см. рис. 5.1) матрица М будет выглядеть следующим образом:

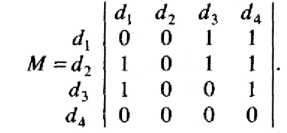
Отличие столбцов матриц М и В объясняется тем, что в матрице Мучитывается смысловое отношение Я между информационными элементами, а в матрице В - только непосредственно Ло- Например, элемент ^4 в матрице Мдостижим из элементов ф\, й?2 и й?з, т.е. й\Яс1^, й?2^4 и с1т,Яс1^, в то время как в матрице В для этих элементов </4 достижим только из ^3, т.е. только й?3-/?0^4-Из анализа матрицы М следует, что элемент (12 является входным, ^4- выходным, остальные - промежуточные. На основе матрицы М строится информационный граф О8 (А Я) системы, структурированный по входным (М\), промежуточным (N2) и выходным (N3) наборам информационных элементов и полученный из анализа множества элементов предшествования А(ф) и достижимости Я (ф) (рис. 5.2).

В общем случае информационный граф системы в отличие от вычисленного графа может иметь контуры и петли, что объясняется необходимостью повторного обращения к отдельным элементам данных.

Информационный граф системы <7$ (АЛ) структурируется по уровням (N1, N2, N3) с использованием итерационной процедуры, что позволяет определить информационные входы и выходы системы, выделить основные этапы обработки данных, их последова-

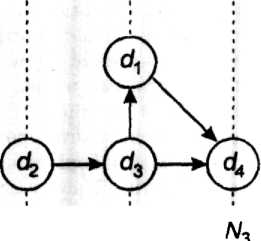
Рис. 5.2. Информационный граф Оц (Б,К)

тельность и циклы обработки на каждом уровне. Кроме того, удаляются избыточные (лишние) дуги и элементы. Граф, получаемый после структуризации по наборам информационных элементов и удаления избыточных элементов и связей, определяет каноническую структуру информационной базы. Таким образом, каноническая структура задает логически неизбыточную информационную базу. Выделение наборов элементов данных по уровням позволяет объединить множество значений конечных элементов в логические записи и тем самым упорядочить их в памяти ЭВМ.

От канонической структуры переходят к логической структуре информационной базы, а затем к физической организации информационных массивов. Каноническая структура служит также основой для автоматизации основных процессов предпроект-ного анализа предметных областей систем управления.

Процедуры хранения, актуализации и извлечения данных непосредственно связаны с базами данных, поэтому логический уровень этих процедур определяется моделями баз данных.

⇐Процесс накопления данных | Информационные системы и технологии в зкономике | Базы данных⇒