В зависимости от вида вычислительной системы (одно- или многомашинной), в которой организуется и планируется процесс обработки данных, возможны различные методы организации и обслуживания очередей заданий. При этом преследуется цель получить наилучшие значения таких показателей, как производительность, загруженность ресурсов, время простоя, пропускная способность, время ожидания в очереди заданий (задание не должно ожидать вечно).

При организации обслуживания вычислительных задач на логическом уровне создается модель задачи обслуживания, которая может иметь как прямой, так и обратной (оптимизационный) характер. При постановке прямой задачи се условиями являются значения параметров вычислительной системы, а решением - показатели эффективности ОВП. При постановке обратной, или оптимизационной, задачи условиями являются значения показателей (или показателя) эффективности ОВП, а решением - параметры вычислительной системы (ВС).

В общем случае момент появления заданий в вычислительной системе является случайным, случайным является и момент окончания вычислительной обработки, так как заранее не известно, по какому алгоритму, а значит, и как долго будет протекать процесс. Тем не менее для конкретной системы управления всегда можно получить статистические данные о среднем количестве поступающих в единицу времени на обработку в ВС вычислительных задач (заданий), а также о среднем времени решения одной задачи. Наличие этих данных позволяет формально рассмотреть процедуру организации вычислительного процесса с помощью теории систем массового обслуживания (СМО). В этой теории при разработке аналитических моделей широко используются понятия и методы теории вероятности.

На рис. 4.2 изображена схема организации многомашинной вычислительной системы, где упорядочение очереди из потока заданий осуществляется диспетчером Д1. а ее обслуживание ЭВМ - через диспетчера Д2.

Такая система может быть охарактеризована как система с дискретными состояниями и непрерывным временем. Под диск

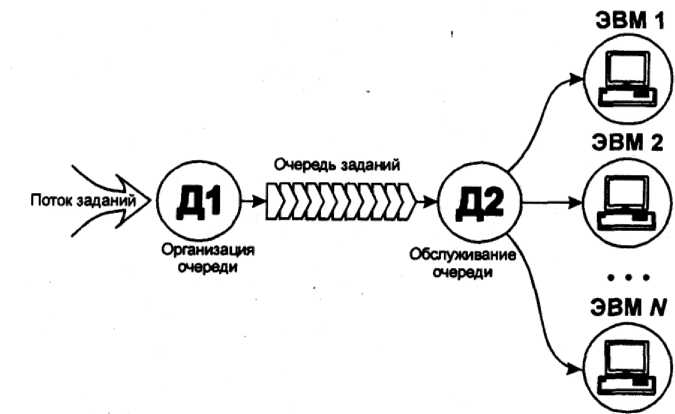
Рис. 4.2. Схема организации обслуживания заданий в многомашинной вычислительной системе ретными состояниями понимается то, что в любой момент система может находиться только в одном состоянии, а число состояний ограничено (может быть пронумеровано). Говоря о непрерывном времени, подразумевают, что границы переходов из состояния в состояние не фиксированы заранее, а неопределенны, случайны, и переход может произойти в принципе в любой момент.

Система (в нашем случае вычислительная система) изменяет свои состояния под действием потока заявок (заданий) - поступающие заявки (задания) увеличивают очередь. Число заданий в очереди плюс число заданий, которые обрабатываются ЭВМ (т.е. число заданий в системе)., - это характеристика состояния системы. Очередь уменьшается, как только одна из машин заканчивает обработку (обслуживание) задания. Тотчас же на эту ЭВМ из очереди поступает стоящее впереди (или по какому-либо другому приоритету) задание и очередь уменьшается. Устройства обработки заявок в теории систем массового обслуживания называют каналами обслуживания. В этой теории поток заданий (заявок на обслуживание) характеризуется интенсивностью X - средним количеством заявок, поступающих в единицу времени

(например, в час). Среднее время обслуживания (обработки) одного задания /₀бсл определяет так называемую интенсивность потока обслуживания ц:

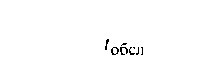
т. е. Ц, показывает, сколько в среднем заданий обслуживается системой в единицу времени. Следует напомнить, что моменты появления заданий и моменты окончания обслуживания случайны, а интенсивности потоков являются результатом статистической обработки случайных событий на достаточно длинном промежутке времени и позволяют получить хотя и приближенные, но хорошо обозримые аналитические выражения для расчетов параметров и показателей эффективности системы массового обслуживания.

Пример.

Рассмотрим модель обслуживания вычислительных заданий в системе (см. рис. 4.2), введя следующие предположения:

• в системе протекают марковские случайные процессы;

• потоки событий (появление заданий и окончание их обработки) являются простейшими;

• число заданий в очереди не ограничено, но конечно.

Случайный процесс, протекающий в системе, называется марковским (по фамилии русского математика), если для любого момента времени вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент и не зависят от того, когда и как система пришла в это состояние. Реально марковские случайные процессы в чистом виде в системах не протекают. Тем не менее реальный случайный процесс можно свести при определенных условиях к марковскому. А в этом случае для описания системы можно построить довольно простую математическую модель.

Простейший поток событий характеризуется стационарностью, ординарностью и "беспоследействием'⁷. Стационарность случайного потока событий означает независимость во времени его параметров (например, постоянных интенсивностей Я и ц). Ординарность указывает на то, что события в потоке появляются поодиночке, а "беспоследей-ствие"- на то, что появляющиеся события не зависят друг от друга (т. е. поступившее задание не обязано своим появлением предыдущему).

Третье предположение позволяет не ограничивать длину очереди (например, не более десятью заявками), хотя и содержит в себе требования конечности, т.е. можно посчитать число заявок в очереди.

5,, - в системе п заданий, и они обрабатываются на ЭВМ 1, ЭВМ 2,…, ЭВМ Ы; Б_п+ [ - в системе (л + 1) заданий, п заданий обрабатываются ЭВМ, а одно стоит в очереди; Б_п+2 - в системе (и + 2) заданий, два задания стоят в очереди;

5« + т - в системе (п + т) заданий, т заданий стоят в очереди.

Учитывая, что увеличение числа заявок (заданий) в системе (т.е. номера состояния) происходит под воздействием их потока с интенсивностью X, а уменьшение - под воздействием потока обслуживания с интенсивностью ц, изобразим размеченный граф состояний нашей системы (рис. 4.3).

Рис. 4.3. Граф состояний многоканальной системы обслуживания с неограниченной очередью

Здесь окружности - состояния, дуги со стрелками - направления переходов в следующие состояния. Дугами помечены интенсивности потоков событий, которые заставляют систему менять состояния. Переходы слева направо увеличивают номер состояния (т. е. число заявок в системе), справа налево - наоборот. Как уже указывалось, увеличение числа заявок в системе происходит под воздействием входного потока заявок с постоянной интенсивностью X. Уменьшение числа заявок в системе (уменьшение номера состояния) происходит под воздействием потока обслуживания, интенсивность которого определяется средним временем обслуживания задания одной ЭВМ и числом ЭВМ, участвующих в обработке заданий при данном состоянии системы. Если одна ЭВМ обеспечивает интенсивность потока обслуживания и. (например, в среднем 30 заданий в час), то одновременно работающие две ЭВМ обеспечат интенсивность обслуживания 21. три ЭВМ - Зц, п ЭВМ - щ. Такое увеличение интенсивности обслуживания будет происходить вплоть до состояния когда п заданий параллельно находятся на обработке на п ЭВМ. Появление в этот момент заявки переводит систему в состояние + \, при котором одна заявка стоит в очереди. Появление еще одной - в состояние + 2 и т.д. Интенсивность же потока обслуживания при этом будет оставаться неизменной и равной лц, так как все ЭВМ вычислительной системы уже задействованы.

При исследовании такой вероятностной системы важно знать значение вероятностей состояний, с помощью которых можно вычислить показатели эффективности, такие, как количество заданий в системе, время ожидания обработки, пропускная способность и т.д. Как известно, значение вероятности лежит в пределах от 0 до 1. Так как мы рассматриваем дискретную систему, то в любой момент времени она может находиться только в одном из состояний и, следовательно, сумма вероятностей состояний Р, всегда равна 1, т.е.

где к - число возможных состояний системы;

; - номер состояния.

Для того чтобы определить значение Р, (7), приведенной формулы недостаточно. Кроме нее составляется еще система дифференциальных уравнений Колмогорова, решение которой и дает искомые значения Л'(0- Чаще всего реальные вычислительные системы быстро достигают установившегося режима, и тогда вероятности состояний перестают зависеть от времени и практически показывают, какую долю достаточно длинного промежутка времени система будет находиться в том или ином состоянии. Например, если система имеет три возможных состояния: Р\ = 0,2, Рг = 0,6, Рз = 0,1, то это означает, что в состоянии 8] система в среднем находится 20% времени, в -----60%, а в 5з - 10% времени. Такие не зависимые от времени вероятности называют финальными.

Финальные вероятности системы вычислить уже проще, так как уравнения Колмогорова при этом превращаются в алгебраические.

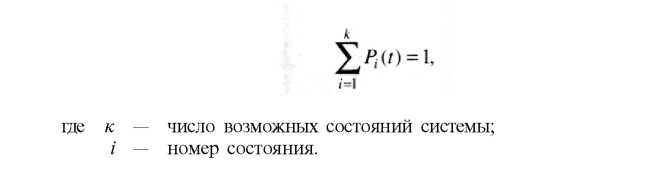
В нашем случае на основе графа (см. рис. 4.3) для определения финальных вероятностей вычислительной системы может быть записана следующая система алгебраических уравнений: ЛРо =(іР\\

(1 /л + Л)Р_[= ЯР₀+ 2цР₂;

(2ц + Х)Р₂= ЛР_{+ ЪцР_ъ;

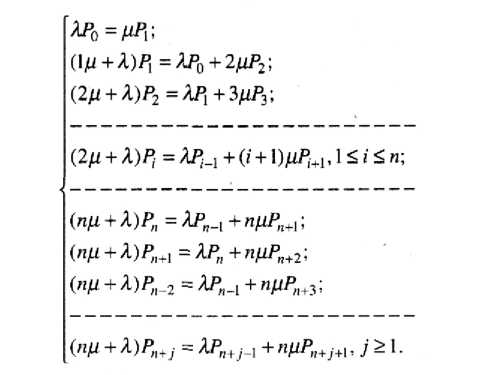
Это система однородных уравнений (свободный член равен нулю), но благодаря тому, что

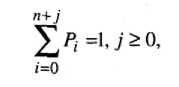
система разрешима. Финальные вероятности состояний системы в результате решения описываются следующими математическими отношениями:

где Р; - вероятность состояния 5",;

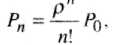
где Р_п- вероятности того, что все ЭВМ заняты;

/У^{П +}1

Практически это выражение говорит о том, что в среднем число заданий, приходящих в вычислительную систему в единицу времени, должно быть меньше числа обрабатываемых заданий в единицу времени всеми ЭВМ системы. Если же - > 1, то очередь растет до бесконечп ности и такая вычислительная система не справится с потоком заданий. Вот тут и могут появиться задания, ожидающие обработки вечно.

Основными показателями эффективности рассматриваемой системы являются: среднее число занятых каналов (т.е. ЭВМ) - к, среднее число заданий в очереди - Р_очи в системе - Ь_сист, среднее время пребывания задания в системе - И'сист^ивочереди - И^,:

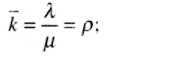
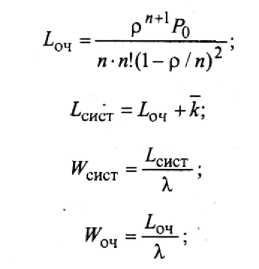
Как видно, полученная математическая модель довольно проста и позволяет легко рассчитать показатели эффективности вычислительной системы. Очевидно, что для уменьшения времени пребывания задания в системе, а значит, и в очереди требуется при заданной интенсивности потока заявок либо увеличивать число обслуживающих ЭВМ, либо уменьшать время обслуживания каждой ЭВМ, либо и то, и другое вместе.

С помощью теории массового обслуживания можно получить аналитические выражения и при других дисциплинах обслуживания очереди и конфигурациях вычислительной системы. Рассматривая модель обслуживания заданий, мы исходим из предположения, что процессы в системе - марковские, а потоки - простейшие. Если эти предположения неверны, то получить аналитические выражения трудно, а чаще всего невозможно. Для таких случаев моделирование проводится с помощью метода статистических испытаний (метода Монте-Карло), который позволяет создать алгоритмическую модель, включающую элементы случайности, и путем ее многократного запуска получить статистические данные, обработка которых дает значения финальных вероятностей состояний.

Как указывалось, организация очереди, поддержание ее структуры возлагаются на диспетчера Д1, а передача заданий из очереди на обработку в вычислительные машины, поддержание дисциплины обслуживания в очереди (поддержка системы приоритетов) осуществляются диспетчером Д2 (см. рис. 4.2). В вычислительной системе диспетчеры реализуются в виде управляющих программ, входящих в состав операционных систем ЭВМ.

Появление заданий при технологическом процессе обработки данных является случайным, но при решении задачи по про

⇐Организация выислительного процесса | Информационные системы и технологии в зкономике | Организация планирования обработки выислительных зада⇒