Эффективность обслуживания вычислительных задач (их программ) зависит прежде всего от среднего времени обслуживания

?обсл⁼~ ’ поэтому в вычислительной системе (и в многомашинной, и в одномашинной особенно) требуется решать проблему минимизации времени обработки поступивших в систему заданий. Иногда эта проблема трансформируется в задачу максимизации загрузки устройств ЭВМ. являющихся носителями ресурсов.

При решении вычислительной задачи ЭВМ использует свои ресурсы в объеме и последовательности, определяемых алгоритмом решения. К ресурсам ЭВМ относятся объем оперативной и внешней памяти, время работы процессора, время обращения к внешним устройствам (внешняя память, устройства отображения). Естественно, что эти ресурсы ограничены. Поэтому и требуется найти наилучшую последовательность решения поступивших на обработку вычислительных задач. Процесс определения последовательности решения задач во времени называется планированием. При планировании необходимо знать, какие ресурсы и в каком количестве требует каждая из поступивших задач. Анализ потребности задачи в ресурсах производится на основе ее программы решения. Программа состоит, как правило, из ограниченного набора процедур (по крайней мере к этому стремятся) с известными для данной ВС затратами ресурсов. После анализа поступивших программ решения задач становится ясно, какая задача каких ресурсов требует и в каком объеме. Критерии, используемые при планировании, зависят от степени определенноети алгоритмов решаемых задач. Крайних случаев два: порядок использования устройств ЭВМ при решении задач строго задан их алгоритмами, а порядок использования устройств ВС в задачах заранее не известен. Для первого случая приемлем критерий минимизации суммарного времени решения вычислительных задач, для второго - максимизации загрузки устройств ВС.

Пример.

Рассмотрим модель планирования вычислительного процесса при минимизации суммарного времени [21].

Обозначим ресурсы вычислительной системы через Лі, ІЇ2, -, К^п-Каждая программа решения задачи обработки данных включает типовые процедуры из набора Пі, Пг, …, П_т. Тогда матрица Г ресурсозатрат, приведенных к времени, будет выглядеть так:

знание матриц ресурсозатрат при выполнении программ позволяет вычислить суммарные затраты каждого из ресурсов по всем программам решения вычислительных задач, поступивших в ВС, и составить их матрицу ресурсозатрат. Обозначим поступившие в ВС программы решения задач через Зь З2, ■•■,3т; - затраты у-го ресурса на выполнение г-й задачи (г = 1,…, т; ]= 1,…, п)\ Я\, Кг, …, - ресурсы ВС. Матрица ресурсозатрат по задачам запишется в виде

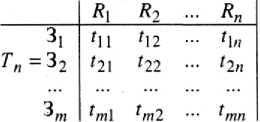
В вычислительной системе ресурсы чаще всего используются последовательно. Поэтому на основе матрицы Т_пможно выделить последовательность прохождения через обработку задач, которая минимизирует суммарное время. Одним из методов нахождения такой последовательности, т. е. планирования, является метод решения задачи Джонсона [32], относящийся к теории расписаний и дающий эффективный и строгий алгоритм. При этом учитываются следующие ограничения:

• для любого устройства ВС выполнение последующей вычислительной задачи не может начаться до окончания предыдущей;

• каждое устройство в данный момент может выполнять только одну вычислительную задачу;

• начавшееся выполнение задачи не должно прерываться до полного его завершения.

Если в процессе обработки данных используется п устройств (ресурсов) ВС, нахождение оптимальной последовательности поступающих на решение т задач, минимизирующих суммарное время обработки, потребует перебора (га!)” вариантов. Например, если в ВС поступило всего шесть заданий (т = 6), использующих всего два ресурса (п - 2), то для нахождения оптимальной последовательности после составления матрицы Т„ потребуется произвести (6!) переборов, т.е. 518400. Если же т - 10, то потребуется порядка 10¹³переборов. Ясно, что даже для ЭВМ это многовато.

Алгоритм Джонсона, полученный для п = 2, требует перебора только от (т + 1) / 2 вариантов, т.е. для нашего примера (т = 6) необходимо будет проделать 21 перебор, что значительно меньше, чем 518400. При и > 2 задачу планирования по критерию минимума суммарного времени обработки сводят к задаче Джонсона путем преобразования матрицы Г,,. Например, если п = 3 (т. е. три ресурса), то производится попарное сложение первого и второго, второго и третьего столбцов и таким образом получают двухстолбцовую матрицу Т_п. После преобразования следует проверить, выполняются ли вышеперечисленные условия. Если это не так, то задача планирования не имеет строгого решения и используют эвристические алгоритмы.

Для пояснения алгоритма Джонсона представим матрицу Т„ как двухстолбцовую:

Алгоритм Джонсона состоит в следующем.

1. В матрице Т„ определяется /_mjn-min{/)1, t\2, …, trnl}2. Из задать …, 3_mвыбираются задачи, для которых ресурсоем-кость хотя бы по одному устройству была равна t_mm, т.е. в данном случае выбирают задачи 3/, у которых хотя бы одна из двух ty= f_m;_n. (Напомним, что / - это номер задачи,у - номер устройства, i = 1,…, т,

j=^l>2.)

3. Задачи группируют по минимальному времени их исполнения tmm на первом и втором устройствах, т.е. 3,- (/minfa) и 3,- (tu, ?min)4. В начало последовательности обрабатываемых задач ставят 3, (?min> to), В КОНИД - 3/ ( tu, t_m\_n).

5. Задачи, вставленные в последовательность обрабатываемых задач, исключаются из матрицы Т„.

6. Для новой матрицы повторяются пункты 1-3.

7. Задачи 3,- (tmin, fß) И 3; (ln, ?min) , полученные из новой матрицы, ставятся в середину составленной ранее последовательности обрабатываемых задач и т. д.

В основе эвристических алгоритмов лежат процедуры выбора из поступивших задач наиболее трудоемких и расположения их в порядке убывания времени выполнения.

При планировании по критерию максимума загрузки устройств вычислительной системы матрицы ресурсоемкости преобразуются в матрицы загрузки устройств. Из этих матриц формируют по каждому устройству потоки задач, выборки из которых позволяют сформировать оптимальную последовательность задач, подлежащих обработке.

Реализация функций и алгоритмов планирования вычислительного процесса происходит с помощью управляющих программ операционной системы ВС. Программа планировщик определяет ресурсоемкость каждой поступившей на обработку задачи и располагает их в оптимальной последовательности. Подключение ресурсов в требуемых объемах к программам выполнения задач осуществляет по запросу планировщика управляющая программа супервизор, которая тоже входит в состав операционной системы.

Таким образом, одной из важнейших процедур информационного процесса обработки данных является организация вычислительного процесса, т.е. обслуживание поступающих на обработку заданий (очередей) и планирование (оптимизация после довательности) их обработки. На программно-аппаратном уровне эти функции выполняют специальные управляющие программы, являющиеся составной частью операционных систем, т. е. систем, организующих выполнение компьютером операций обработки данных.

Разнообразие методов и функций, используемых в алгоритмах организации вычислительного процесса, зависит от допустимых режимов обработки данных в ВС. В наиболее простой ВС, такой, как персональный компьютер (ПК), не требуется управление очередями заданий и планирование вычислительных работ. В ПК применяют в основном однопрограммный режим работы, поэтому их операционные системы не имеют в своем составе программ диспетчирования, планировщика и супервизора. Но в более мощных ЭВМ, таких, как серверы и особенно мейнфреймы, подобные управляющие программы оказывают решающее влияние на работоспособность и надежность ВС. Например, к и№Х-серверам могут обращаться с заданиями одновременно сотни пользователей, а к мэйнфреймам типа 8/390 - тысячи.

⇐Организацияобслуживания выислительных зада | Информационные системы и технологии в зкономике | Преобразование данных⇒