В компьютерной графике все, что относится к двумерному случаю, принято обозначать символом 2Б (2-Шшеп8Іоп). Допустим, на плоскости введена прямолинейная координатная система. Тогда каждой точке М ставится в соответствие упорядочен-' ная пара чисел (х, у) ее координат (рис. 4.26).

Рис. 4.26. Точка в прямоугольной системе координат

Вводя на плоскости еще одну прямолинейную систему координат, мы ставим в соответствие той же точке М другую пару чисел - (х*, у*).

Переход от одной прямолинейной координатной системы на плоскости к другой описывается следующими соотношениями: х* = ах + ру + X; у* = ух + 8у + 0,, где а, Р, у,Х, ц - произвольные числа, связанные неравенством

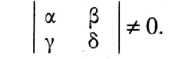
В аффинных (от лат. аґйпіз - родственный) преобразованиях* плоскости особую роль играют несколько важных частных случаев, имеющих хорошо прослеживаемые геометрические характеристики.

* Аффинная геометрия - раздел геометрии, в котором изучаются свойства фигур на плоскости (или в пространстве), сохраняющиеся при любых аффинных преобразованиях плоскости (или пространства), т.е. инвариантные относительно таких преобразований.

При исследовании геометрического смысла числовых коэффициентов в формулах, помеченных символом «*», для этих случаев удобно считать, что заданная система координат является прямоугольной декартовой.

Рассмотрим простейшие аффинные преобразования.

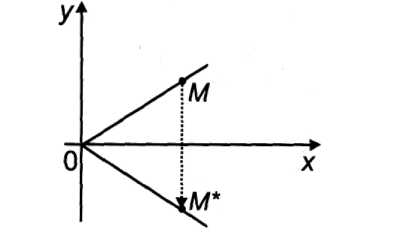
А. Поворот (вокруг начальной точки на угол ф) (рис. 4.27) описывается формулами: х* = лтсоэф -^пф, у* = ;шпф + ^соэф.

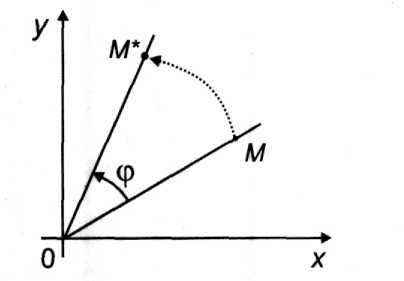
Б. Растяжение (сжатие) вдоль координатных осей можно задать так: х* - ах, у* = 6у, а > 0, 8 > 0.

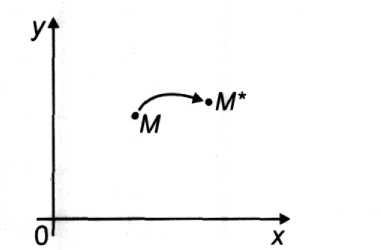
Рис. 4.28. Растяжение вдоль осей Растяжение (сжатие) вдоль оси абсцисс обеспечивается при условии, что а >1 (а < 1). На рис. 4.28 а =5 > 1.

В. Отражение (относительно оси абсцисс) (рис. 4.29) задается при помощи формул: х *= х; у * = - у.

Г. На рис. 4.30 вектор переноса ММ* имеет координаты X и {Д.. Перенос обеспечивают соотношения: х* = х + X; у* = у + ц.

Выбор этих четырех частных случаев определяется двумя обстоятельствами.

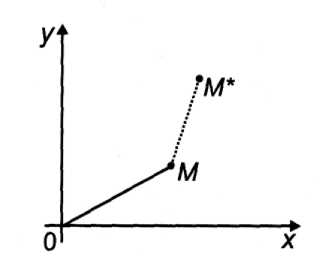
Рис. 4.30. Перенос точки Каждое из приведенных выше преобразований имеет простой и наглядный геометрический смысл (геометрическим смыслом наделены и постоянные числа, входящие в приведенные формулы).

Как доказывается в курсе аналитической геометрии, любое преобразование вида (*) всегда можно представить как последо вательное использование (суперпозицию) простейших преобразований вида А, Б, В и Г (или части этих преобразований).

Таким образом, справедливо следующее важное свойство аффинных преобразований плоскости: любое отображение вида (*) можно описать при помощи отображений, задаваемых формулами для случаев А, Б, В и Г.

Для эффективного использования этих формул в задачах компьютерной графики более удобной является их матричная запись. Матрицы, соответствующие случаям А, Б и В, строятся легко и имеют следующий вид:

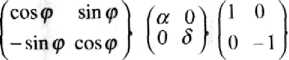
Однако для решения задач компьютерной графики весьма желательно охватить матричным подходом все четыре простейших преобразования (в том числе и перенос), а значит, и общее аффинное преобразование. Этого можно достичь, например, так: перейти к описанию произвольной точки на плоскости, не упорядоченной парой чисел, как это было сделано выше, а упорядоченной тройкой чисел.

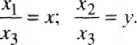
При решении задач компьютерной графики однородные координаты обычно вводятся так: произвольной точке М (х, у) на плоскости ставится в соответствие точка М*(х, у, 1) в пространстве (рис. 4.31).

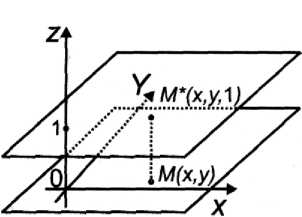
Рис. 4.31. Преобразование координат точки на плоскости в однородные координаты

Заметим, что производная точка на прямой, соединяющей начало координат, точку 0(0, 0, 0) с точкой М*(х, у, 1), может быть задана тройкой чисел вида (1гх, Ну, И). Будем считать, что Вектор с координатами Нх, Ну, Н является направляющим вектором прямой, соединяющей точки 0(0, 0, 0) и М*(х, у, 1). Эта прямая пересекает плоскость г = 1 в точке (х, у, 1), которая однозначно определяет точку (х, у) координатной плоскости ху. Тем самым между произвольной точкой с координатами (х, у) и множеством троек чисел вида (Нх, Ну, Н), Н * 0, устанавливается (взаимно однозначное) соответствие, позволяющее считать числа Нх, Ну, Н новыми координатами этой точки.

В проективной геометрии для однородных координат принято следующее обозначение: х : у : 1 или более общо: х\ / хі :хз (напомним, что здесь непременно требуется, чтобы числа х\, хг, х$ одновременно в нуль не обращались).

Применение однородных координат оказывается удобным уже при решении простейших задач.

Рассмотрим, например, вопросы, связанные с изменением масштаба. Если устройство отображения работает только с целыми числами (или если необходимо работать только с целыми числами), то для произвольного значения Н (например, Н - 1) точку с однородными координатами (0,5 0,1 2,5) представить нельзя. Однако при разумном выборе Н можно добиться того, чтобы координаты этой точки были целыми числами. В частности, при Н = 10 для рассматриваемого примера имеем: (5 1 25).

Рассмотрим другой случай. Чтобы результаты преобразования не приводили к арифметическому переполнению, для точки с координатами (80 000 40 000 1000) можно взять, например, к = 0,001. В результате получим: (80 40 1).

Приведенные примеры показывают полезность использования однородных координат при проведении расчетов. Однако основной целью введения однородных координат в компьютерной графике является их несомненное удобство в применении к геометрическим преобразованиям.

При помощи троек однородных координат и матриц третьего порядка можно описать любое аффинное преобразование плоскости.

В самом деле, считая к - \ сравним две записи: помеченную символом * и матричную:

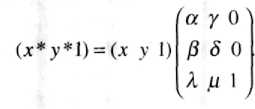
Нетрудно заметить, что после перемножения выражений, стоящих в правой части последнего соотношения, мы получим обе формулы (*) и тождество 1 = 1.

Тем самым сравниваемые записи можно считать равносильными.

Элементы произвольной матрицы аффинного преобразования не несут в себе явно выраженного геометрического смысла. Поэтому чтобы реализовать то или иное отображение, т.е. найти элементы соответствующей матрицы по заданному геометрическому описанию, необходимы специальные приемы. Обычно построение этой матрицы в соответствии со сложностью рассматриваемой задачи и с описанными выше частными случаями разбивают на несколько этапов.

На каждом этапе ищется матрица, соответствующая тому или иному из выделенных выше случаев А, Б, В и Г, обладающих хорошо выраженными геометрическими свойствами.

Выпишем соответствующие матрицы третьего порядка.

А. Матрица вращения (rotation):

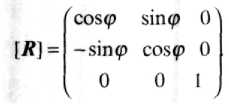
Б. Матрица растяжения (сжатия) (dilatation):

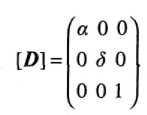
В. Матрица отражения (reflection):

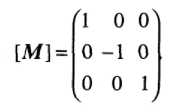
Г. Матрица переноса (translation):

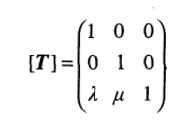
Эти матрицы трактуются как составляющие общей матрицы, преобразующей исходную матрицу А графического объекта в матрицу А* преобразованного объекта.

Общая матрица преобразования при известных у, X, а, (3 и ц получается перемножением матриц простейших преобразований Основные свойства матричных преобразований при переходе к трехмерному (3Б) преобразованию сохраняются, однако более сложной становится операция вращения, требующая задания оси вращения. Напомним, что однородное представление трехмерной точки имеет вид: (Их, Ну, hz, К).

Наличие точных математических моделей графических объектов позволяет относительно легко отображать их на экране монитора, а вычисленные матрицы преобразований дают возможность манипуляции этими объектами на экране как в статике, так и в динамике.

Но далеко не всегда удается получить точное функциональное описание объекта. Чаще всего оказывается возможным вы числить только ряд точек графической фигуры. И тогда возникает задача плавного соединения (а не прямыми) этих точек для восстановления на экране изображения воспроизводимой фигуры. Эта задача в компьютерной графике решается с помощью геометрических сплайнов, или сплайн-функций [38].

СПЛАЙН-ФУНКЦИИ

Сам термин "сплайн" происходит от английского spline. Именно так называется гибкая полоска стали, при помощи которой чертежники проводили через заданные точки плавные кривые. В былые времена подобный способ построения плавных обводов различных тел, таких, как, например, корпус корабля, кузов автомобиля, а потом фюзеляж или крыло самолета, был довольно широко распространен в практике машиностроения. В результате форма тела задавалась при помощи набора очень точно изготовленных сечений - плазов. Появление компьютеров позволило перейти от этого, плазово-шаб-лонного, метода к более эффективному способу задания поверхности обтекаемого тела. В основе этого подхода к описанию поверхностей лежит использование относительно несложных формул сплайн-функций, позволяющих восстанавливать облик изделия с необходимой точностью.

Рассмотрим сплайны, в построении которых используются кубические (для одномерных сплайнов - сплайновых кривых) и бикубические (для двумерных сплайнов сплайновых поверхностей) многочлены. В компьютерной графике подобные сплайны применяются наиболее часто.

Достаточно типичной является следующая задача: по заданному массиву точек на плоскости (2D) или в пространстве (3D) построить кривую, проходящую либо через все эти точки (задача интерполяции), либо вблизи от этих точек (задача сглаживания).

Совершенно естественно возникают вопросы: в каком классе кривых искать решение поставленной задачи? как искать?

А. Случай одной переменной. Обратимся для определенности к задаче интерполяции и начнем рассмотрение с обсуждения правил выбора класса кривых. Ясно, что допустимый класс кривых должен быть таким, чтобы решение задачи было единственным (это обстоятельство сильно помогает в преодолении многих труд ностей поиска). Кроме того, желательно, чтобы построенная кривая изменялась плавно.

Пусть на плоскости задан набор точек (х/,у/), і = 0,1,…,от, таких, что хо < х\ <… <х_ті < х_т(рис. 4.32).

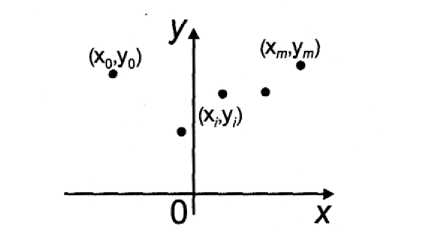
Рис. 4.32. Набор точек на плоскости Благодаря тому, что точки заданного набора занумерованы в порядке возрастания их абсцисс, можно искать кривую в классе графиков функции, а основные моменты сглаживания этого дискретного набора описывать, ограничившись многочленами.

Как известно из курса математического анализа, существует интерполяционный многочлен Лагранжа:

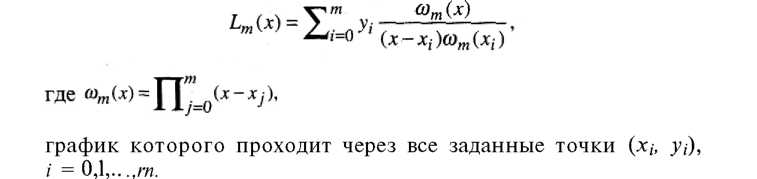
Это обстоятельство и простота описания (заметим, что многочлен однозначно определяется набором своих коэффициентов; в данном случае их число совпадает с количеством точек в заданном наборе) являются несомненными достоинствами построенного интерполяционного многочлена (разумеется, есть и другие).

Однако полезно остановиться и на некоторых недостатках предложенного подхода.

1. Степень многочлена Лагранжа на единицу меньше числа заданных точек. Поэтому чем больше точек задано, тем выше степень такого многочлена. И хотя график интерполяционного члена Лагранжа всегда будет проходить через все точки массива, его уклонение (от ожидаемого) может оказаться довольно значительным.

2. Изменение одной точки (ситуация, довольно часто встречающаяся на практике) требует полного пересчета коэффициентов интерполяционного многочлена и к тому же может существенно повлиять на вид задаваемой им кривой.

Приближенную кривую можно построить и совсем просто: если последовательно соединить точки заданного набора прямолинейными отрезками, то в результате получится ломаная (рис. 4.33).

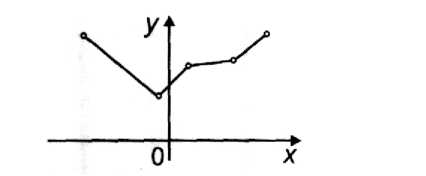
Рис. 4.33. Приближенная ломаная При такой, кусочно-линейной, интерполяции требуется найти всего 2т чисел (каждый прямолинейный отрезок определяется ровно двумя коэффициентами), но, к сожалению, построенная таким образом аппроксимирующая кусочно-линейная функция не обладает нужной гладкостью: уже первая производная этой функции терпит разрывы в узлах интерполяции.

Рассмотрев эти две крайние ситуации, попробуем найти класс функций, которые сохранили бы перечисленные выше достоинства обоих подходов и были бы в известной степени свободны от их недостатков.

Для этого будем использовать многочлены (как и в случае 1) и строить их последовательно, звено за звеном (как и в случае 2). В результате получится так называемый полиномиальный мно-гозвенник. При подобном подходе важно правильно выбрать степени привлекаемых многочленов, а для плавного изменения результирующей кривой необходимо еще тщательно подобрать коэффициенты многочленов (из условия гладкого сопряжения соседних звеньев). То, что получится в результате описанных условий, называют сплайн-функциями или просто сплайнами.

Для того чтобы понять, какое отношение имеют сплайн-функции к чертежным сплайнам, возьмем гибкую стальную линейку, поставим ее на ребро и, закрепив один из концов в заданной точке, поместим ее между опорами, которые располагаются в плоскости ОХУ в точках (х,-, у,), і = 0,1 ,…, т, где хо < хі<…<х_т-і <х_т(рис. 4.34).

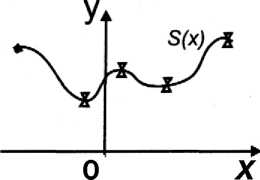
Рис. 4.34. Приближение сплайном Интересно отметить, что функция у - 5(х), описывающая профиль линейки, обладает следующими свойствами:

• с довольно большой точностью часть графика этой функции, заключенную между любыми двумя соседними опорами, можно считать многочленом третьей степени;

• на всем промежутке [хо,х_т] функция у = S(x) дважды непрерывно дифференцируемая.

Построенная функция S(x) относится к так называемым интерполяционным кубическим сплайнам.

Перейдем, однако, к точным формулировкам.

Интерполяционным кубическим сплайном называется функция S(x), обладающая следующими свойствами:

1) график функции проходит через каждую точку массива, Я*,) = у и - 0,1,..,,т;

2) на каждом из отрезков [х/, Х/+1], i - 0,1,…,т-1, функция является многочленом третьей степени:

3) на всем отрезке задания [хо, х_т] функция 5(х_г) имеет непрерывную вторую производную.

На каждом из отрезков [х,-, *,+1] сплайн Б(х) определяется четырьмя коэффициентами, поэтому для полного построения на всем отрезке задания необходимо найти 4т чисел.

Условие 3 будет выполнено, если потребовать непрерывности сплайнов во всех внутренних узлах х/, I = 0,1,…,т-1 (это дает т~\ условий на коэффициенты), а также его первой (т-1 условий) и второй (еще т- \ условий) производных в этих узлах. Вместе с условием 1 получаем равенство

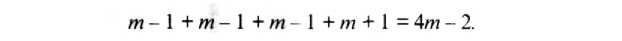
Недостающие два условия для полного определения коэффициентов можно получить, задав, например, значения первых производных на концах отрезка [хо, х_т] (граничные условия):

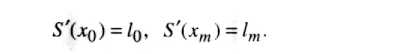
Существуют граничные условия и других типов.

Б. Случай двух переменных. Более сложная задача построения по заданному набору точек в трехмерном пространстве интерполяционной функции двух переменных решается похожим образом. Определим прежде всего интерполяционный бикубический сплайн.

Пусть на плоскости задан набор из (т + 1)(и + 1) точек (рис. 4.35)

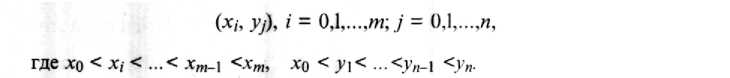
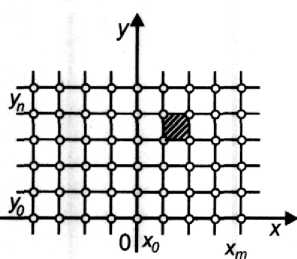
Рис. 4.35. Набор (т + 1)(и + 1) точек на плоскости

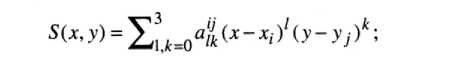
Добавим к каждой паре (х/, у]) третью координату ~,у (х/, ур гф. Тем самым получаем массив (х_г-, ур гф, I = 0,1,…, га;у= 0,1,…, п.

Прежде чем строить поверхность, проходящую через все точки заданного массива, определим функцию, графиком которой будет эта поверхность.

Интерполяционным бикубическим сплайном называется функция двух переменных S (х, у), обладающая следующими свойствами:

1) график функции проходит через каждую точку заданного массива: 5(х_г-,^,-) = г,-, I = 0,1,…, т; ] = 0,1,…, и;

2) на каждом частичном прямоугольнике [х/, х/+1] х у,-, У]+\\,

I = 0,1,…, т-1;]= 0,1,…, и-1, функция представляет собой многочлен третьей степени по каждой из переменных:

3) на всем прямоугольнике задания [хо, х_т] х [уо, Уп] функция S(x, у) имеет по каждой переменной непрерывную вторую производную.

Для того чтобы построить по заданному массиву {(х,-, ур гф} интерполяционный бикубический сплайн, достаточно определить все \6тпкоэффициентов. Как и в одномерном случае, отыскание коэффициентов сплайн-функции сводится к построению решения системы линейных уравнений, связывающих искомые коэффициенты .

Последняя возникает из условий 1 и 3, после добавления к ним недостающих соотношений путем задания значений произвольной искомой функции в граничных узлах прямоугольника [хо, х_т] х [уо> Уп] (или иных соображений).

Достоинства предложенного способа несомненны: для решения линейных систем, возникающих в ходе построения сплайн-функций, существует много эффективных методов, к тому же эти системы достаточно просты; графики построенных сплайн-функций проходят через все заданные точки, полностью сохраняя первоначально заданную информацию.

Вместе с тем изменение лишь одной точки (случай на практике довольно типичный) при описанном подходе заставляет пересчитывать заново, как правило, все коэффициенты.

Однако во многих задачах исходный набор точек задается приближенно, и, значит, требование неукоснительного прохождения графика искомой функции через каждую точку этого набора оказывается излишним. В этом случае используются методы сглаживания, при которых можно отказаться от требования строго однозначного проектирования искомой кривой на координатную ось, а поверхности - на координатную плоскость.

⇐Отображение данных | Информационные системы и технологии в зкономике | Реализация процедур отображения⇒