Скорость передачи информации, а ее предельно допустимое значение для данного канала называют емкостью канала, относится к фундаментальным понятиям теории связи, она служит одной из главных характеристик канала передачи информации. Оценка скорости передачи информации и предельных возможностей канала связи представляет большой практический и теоретический интерес.

Рассматривая процесс передачи информации в общих чертах, можно предположить, что основными факторами, ограничивающими скорость передачи информации, являются полоса пропускания Г и уровень помех.

Существует фундаментальная теорема о выборках, которая доказывает, что сигнал, не содержащий в своем спектре частот выше значения Г, может представляться 2Г независимыми значениями в секунду, а совокупность значений, отстоящих друг от друга на Т секунд, определяет непрерывный сигнал полностью. Заметим, что выборкой является отсчет амплитуды сигнала в определенный момент (на рис. 6.12, а можно увидеть эти выборки, проводимые через интервал 1/2 Р).

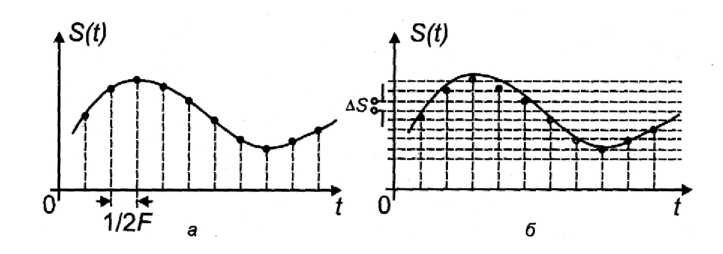
Рис. 6.12. Представление непрерывного сигнала в виде дискретных отсчетов (выборок), взятых через интервал 1/2Р (а) и квантованных по амплитуде (б)

Термин выборки происходит от английского слова sample (в переводе - образец, модель, проба), теорему о выборках называют также теоремой отсчетов.

Эта теорема позволяет на интервале Т заменить непрерывный сигнал с ограниченным спектром последовательностью его дискретных значений, причем их нужно не бесконечное число, а вполне определенное, равное 2РТ. Уровень шумов (помех) не позволяет точно определить амплитуду сигнала и в этом смысле вносит некоторую неопределенность в значение отсчетов сигнала.

Максимально возможная скорость передачи информации по каналу связи при фиксированных ограничениях называется емкостью канала, обозначается буквой С и имеет размерность бит/с.

Рассмотрим соотношение для емкости канала связи, являющееся фундаментальным соотношением в теории связи. Оно позволяет понять некоторые принципиальные зависимости при передаче информации вообще.

Напомним, что количество информации /, снимающее неопределенность о состоянии объекта с Ь равновероятными состояниями, рассчитывается по формуле

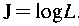
Основание логарифма здесь не имеет значения. Если основание равно 2, то единицей измерения количества информации оказывается бит.

Определим количество различных сообщений, которое можно составить из п элементов, принимающих любые из т различных фиксированных состояний. Из ансамбля п элементов, каждый из которых может находиться в одном из т фиксированных состояний, можно составить т " различных комбинаций, т. е. Ь = т^п. Тогда:

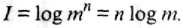
При полосе Г наибольшее число отсчетов сигнала равно 2Г в единицу времени или2^Тза время Т, т. е. п = 2РТ.

Если бы шума не существовало, то число дискретных уровней сигнала было бы бесконечным. В случае наличия шума последний определяет степень различимости отдельных уровней амплитуды сигнала. Так как мощность является усредненной характеристикой амплитуды, число различимых уровней сигнала по мощности равно (Р_с+ Р_ш)/ Р_ш, а по амплитуде соответственно т- л1(^рс +Р_Ш)/Р_Ш> где Р_с- мощность сигнала; Ли- мощность шума. Тогда емкость канала рассчитывается по формуле

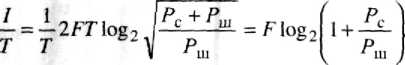
Итак, емкость канала ограничивается двумя величинами: шириной полосы канала и шумом. Приведенное соотношение известно как формула Хартли - Шеннона и считается основной в теории информации.

Полоса частот и мощность сигнала входят в формулу таким образом, что да я С - const при сужении полосы необходимо увеличивать мощность сигнала, и наоборот.

Емкость канала является максимальной величиной скорости. Чтобы достигнуть такой скорости передачи, информация должна быть закодирована наиболее эффективным образом. Утверждение, что такое кодирование возможно, является важнейшим результатом созданной К.Э. Шенноном теории информации. Шеннон доказал принципиальную возможность существования такого эффективного кодирования, не определив, однако, конкретных путей его реализации. (Отметим, что на практике инженеры часто говорят о емкости канала, подразумевая под этим реальную, а не потенциальную скорость передачи.)

Эффективность систем связи характеризуется параметром, равным скорости передачи информации R на единицу ширины полосы F, т. е. R/F. Для иллюстрации существующих возможностей по созданию эффективных систем связи на рис. 6.13 приведе-

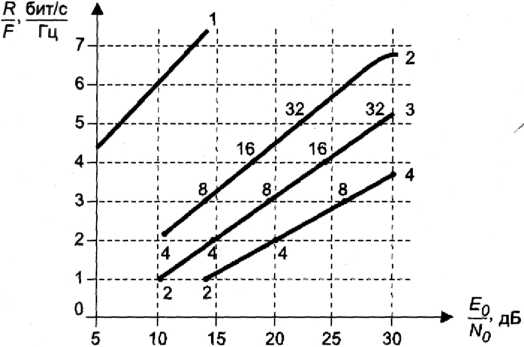
Рис. 6.13. Кривые зависимости эффективности цифровых систем связи при различных модуляциях:

1 - граница Шеннона; 2 - М-ичная фазовая модуляция;

3 - М-ичная амплитудная модуляция; 4 - М-ичная частотная модуляция 6.6.3. КОДИРОВАНИЕ ИНФОРМАЦИИ

Кодированием называется сопоставление алфавитов, а правило, по которому оно проводится, - кодом. Иными словами, кодирование можно определить как представление сообщений в форме, удобной для передачи по данному каналу. Электрический ток в телефонных проводах - это кодированная речь, а звуковые волны речи - это кодированные колебания голосовых связок.

В рассматриваемом нами конкретном случае кодирование есть представление по определенным правилам дискретных сообщений в некоторые комбинации, составленные из определенного числа элементов - символов. Эти элементы называются элементами кода, а число различных элементов, из которых слагаются комбинации, - основанием кода. Элементы кода образуют кодовые комбинации. Например, если мы составляем комбинации из различных сочетаний 0 и 1, то это код с основанием два, или двоичный код. Если все комбинации имеют одинаковое число знаков, код называется равномерным. Широко известный код Морзе - неравномерный код. Правило кодирования обычно выражается кодовой таблицей, в которой каждому символу сообщения ставится в соответствие определенная кодовая комбинация.

Кодовое представление дискретных значений сигнала осуществляется с помощью цифр, но необязательно десятичных. Напомним, что в десятичной системе, называя число, мы указываем, сколько единиц от нуля до девяти имеется в разряде единиц, в разряде десятков, сотен, тысяч и т. д. То же происходит в любой другой системе счисления с другим основанием. В десятичной системе мы пользуемся десятью цифрами: 0,1, 2, 3, 4, 5, 6, 7, 8 и 9. В двоичной системе счисления в нашем распоряжении только две цифры: 0 и 1.

Если пронумеровать все буквы алфавита и необходимые специальные символы и выразить каждую цифру в двоичной системе счисления, получится натуральный двоичный код данного алфавита. Очевидно, что число разрядов в двоичной системе больше, чем в десятичной, так как основание системы счисления меньше.

Число кодовых комбинаций определяется числом дискретных значений сигнала. Например, если в языке 32 буквы (или букв и знаков), то для передачи сообщений на этом языке необходимо иметь 32 различные кодовые комбинации. В десятичной системе это означало бы передачу 32 цифр от 0 до 31. В двоичной системе необходимо составить отличающиеся друг от друга 32 кодовые комбинации, и так как 32 = 2⁵, эти комбинации должны быть из 5 элементов, например 01010, 11111, 11001 и т. д. Число возможных кодовых комбинаций для представления 32 букв колоссально: 32! Один из этих вариантов есть натуральный пятизначный двоичный код, используемый для передачи букв латинского и русского алфавитов. При цифровом кодировании речевых сигналов исходят из практического наблюдения: искажения сигнала невелики, если его изменения представлять 128 амплитудными значениями, т. е. для его передачи необходимо 128 кодовых комбинаций. Для двоичного кода из соотношения 2” = 128 определяем, что длина кодовой комбинации п - 1. Таким образом, для передачи речевых сигналов нужен код с 7-элементными кодовыми комбинациями. Обычно речевой сигнал по спектру ограничен частотой 4000 Гц. В этом случае речь в цифровой форме необходимо передавать со скоростью (вспомним теорему о выборках) 4000 • 2 • 7 = 56 Кбит/с. Заметим, что обычно в комбинацию добавляют один служебный символ, и тогда комбинация становится 8-элементной, а необходимая скорость передачи увеличивается до 64 Кбит/с.

Остановимся также на принципах помехоустойчивого кодирования, играющего чрезвычайно важную роль в развитии средств передачи информации. Отметим, что теория помехоустойчивого кодирования является достаточно сложной, и наши рассуждения носят весьма упрощенный характер.

Основным условием обнаружения и исправления ошибок в принимаемых кодовых комбинациях является избыточность. Поясним это на примере.

Условимся, что необходимо передавать только четыре сообщения: А, Б, В и Г. Для передачи этих сообщений можно составить четыре 2-элементные комбинации: Пусть помехи воздействуют на комбинацию таким образом, что изменяют только один из ее элементов. Если помехе подверглась комбинация 00 и она вследствие этого превратилась в комбинацию 01, то мы не обнаружим ошибку, а будем просто считать, что вместо А передатчик послал Б; и так будет со всеми четырьмя комбинациями.

Теперь введем избыточность. Используем для передачи А, Б, В и Г 3-элементные кодовые комбинации, которых, кстати, может быть всего восемь. Выберем из восьми возможных комбинаций ООО, 001, 010, 100, ПО, 011, 101, 111 (других комбинаций быть не может) только четыре, но так, чтобы они максимально отличались друг от друга: 000, 011, 101, ПО.

Пусть теперь в результате действия помехи изменится один из элементов в любой из выбранных комбинаций. Она не будет идентичной ни одной из наших комбинаций, и мы сразу укажем, что принята ошибочная. Таким образом, для передачи сообщений А, Б, В, Г код 00, 01, 10, 11 годится, но он не помехоустойчив, код же 000, 011, 101, ПО является помехоустойчивым. При этом следует оговориться, что он помехоустойчив только к таким помехам, которые могут привести лишь к однократной ошибке в комбинации. При двукратной ошибке код не помехоустойчив. Для защиты от таких помех сообщений А, Б, В и Г пришлось бы допустить еще большую избыточность, используя 4-элемент-ные кодовые комбинации, т. е. выбрав четыре комбинации из 16 возможных.

Таким образом, обнаружить ошибку невозможно, если любой принятый символ служит сообщением. Ошибки можно обнаружить только в том случае, если на возможные сообщения наложены некоторые ограничения.

Итак, одним из основных достоинств передачи информации в цифровой форме является возможность использования кодированных сигналов и оптимального в заданных условиях способа их приема. Важно, что при цифровой передаче все типы сигналов, такие, как речь, музыка, телевидение, данные, могут объединяться в один общий поток информации, передача которого формализована. Кроме того, уплотнение при одновременном использовании компьютера позволяет эффективнее использовать спектр и время, защитить канал от несанкционированного доступа, объединить в единый процесс передачу цифровой информации и цифровую коммутацию каналов и сообщений.

⇐Модуляция и демодуляция | Информационные системы и технологии в зкономике | Уплотнение информационных потоков⇒