а уравнение прямой как х = t у = a*t + Ь
В общем трехмерном случае параметрическое задание кривой выглядит как х = а + b*t + с * t2 + d*t3 + … у = р + q*t + г * t2 + s*t3 + … z = i + j*t + k * t2 + m*t3 + …
Здесь t является параметром, а остальные буквы - коэффициентами. Максимальная степень, с которой t входит в такие уравнения, называется степенью кривой.
Представьте себе теперь, что параметр t потихоньку растет, а х, у и z в левой части этих формул также меняются, рисуя в пространстве некую трехмерную траекторию. Это и есть кривая, заданная параметрически.
Можно предположить, что чем выше степень кривой, тем более сложную форму можно представить с помощью такой кривой. По крайней мере, гладкая парабола выглядит сложнее, чем просто прямая линия. Формально это так, однако на вычисление таких высокостепенных кривых может уйти много времени и процесс построения кривых (во всяком случае, для нужд моделирования) будет неэффективным.
В MAYA сложная кривая (к примеру, третьей степени), представлена в виде набора сегментов-кривых, каждый из которых задан параметрическим уравнением третьей степени и вычисляется очень быстро.
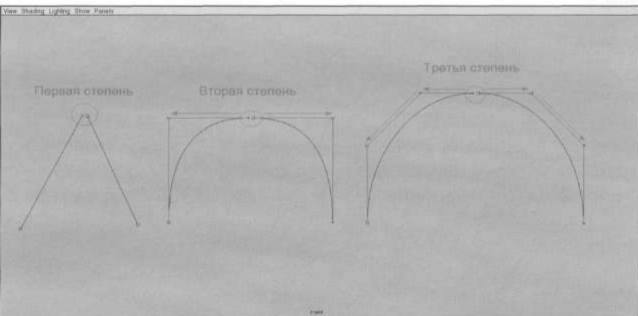
Следующий вопрос состоит в том, насколько гладко можно соединить такие сегменты? Для сегментов кривых первой степени, то есть прямолинейных отрезков, необходимо задать всего две точки, чтобы однозначно определить отрезок. Поэтому два прямых отрезка можно срастить «концами» и получить, таким образом, ломаную кривую.
Для построения отрезка кривой второй степени необходимо задать уже три точки (то есть девять значений координат точек или девять соответствующих коэффициентов в уравнениях). Поэтому для сращивания двух таких сегментов можно использовать крайние точки для соединения концов, а средние точки каждого сегмента использовать для обеспечения гладкого соединения. («Гладко» в данном случае, с точки зрения математики, означает, что касательные для каждого сегмента в точке соединения параллельны)
Однако в компьютерной графике для работы с гладкими формами обычно используют кривые и поверхности третьего порядка. Чтобы задать сегмент кривой третьего порядка надо уже двенадцать коэффициентов или четыре точки в пространстве. Соседние с крайними точки используются гладкой стыковки ,а следующие за ними точки обеспечивают совпадение в точке соединения «кривизны» стыкуемых сегментов.
MAYA поддерживает также работу с кривыми и поверхностями пятой и седьмой степени. Такие объекты используются для дизайна поверхностей, предъявляющих повышенные требования к гладкости и кривизне и применяются, например, в автомобильной промышленности при проектировании и подготовке поверхностей для изготовления реальных прототипов. Для большинства задач, решаемых с помощью MAYA, достаточно кривых и поверхностей первой и третьей степени, поэтому я не буду обсуждать остальные варианты.
Степень и гладкость
Терминологически сложились некоторые названия для объектов первой и третьей степени. Для первых часто употребляются термины «линейная» или «ломаная» кривая (или поверхность). Для третьей степени используются названия «гладкая» или «кубическая» кривая. Таким образом, степень кривой или поверхности является зачастую обозначением ее гладкости.
