Тангенс и кривизна
Разберемся далее с терминами «тангенс» и «кривизна». Эти термины большинство майщиков употребляют, мягко говоря, некорректно, хотя звучит это весьма доходчиво.
«Тангенс» употребляется для обозначения касательной в точке кривой или поверхности. Если для кривой касательная в точке одна, то для поверхностей обычно уточняется конкретное направление в некой касательной плоскости. Слово «тангенс» закрепилось благодаря формуле вычисления касательной, в которой используется тригонометрическая функция - тангенс.
«Кривизна» действительно обозначает кривизну в точке кривой, то есть величину обратно пропорциональную радиусу окружности, максимально удачно вписанной в точку на кривой. Если кривая прямолинейная, то радиус такой окружности бесконечен, а кривизна равна нулю. Кривизну также можно абстрактно представить как скорость изменения касательной в точке.
Термины «кривизна» и «тангенс» часто употребляются при описании концов кривых или краев поверхностей, прилегающих друг к другу. Будем дальше говорить только о кривых, для краткости изложения.
Непрерывность
Если конец одной кривой просто совпадает с началом другой, то говорят, что кривые имеют непрерывность по позиции (positional continuity). Кривые в этом случае, могут встречаться под любым углом. Такой вид непрерывности иногда обозначается как GO.

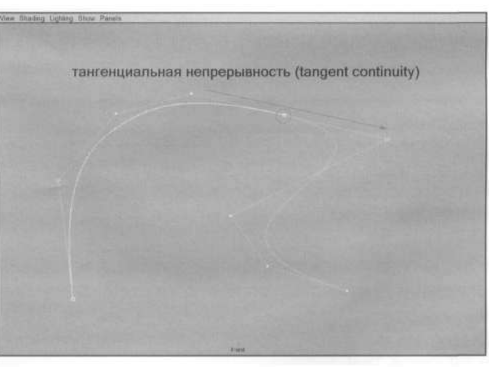
Если кривые соединяются, так что в точке соединения касательные к каждой кривой совпадают (точнее противоположно направлены вдоль одной прямой), то кривые имеют тангенциальную непрерывность (tangent continuity, G1). В народе обычно говорят, что кривые стыкуются (совпадают, сращены) по тангенсу (хотя корректно, наверное, говорить стыкуются по касательной). Однако радиусы кривизны в точке соединения могут быть различны.
Если же в точке соединения совпадает не только тангенс, но и кривизна обеих кривых, то кривые имеют непрерывность по кривизне (curvature continuity, G2). Иначе говоря, стыкуются по кривизне.

Некоторые пытливые умы спросят, а зачем дополнительно добиваться стыковки по кривизне, если по тангенсу и так гладко. Действительно, «наощупь» две поверхности, стыкующиеся по тангенсу, но не по кривизне, будут гладкими, однако при визуализации таких поверхностей рубленый блик в области соединения будет сразу выдавать наличие шва между поверхностями. Иногда, непрерывность по кривизне не требуется, но в общем случае, когда говорят, что поверхности или кривые гладко стыкуются, имеется в виду непрерывность и по тангенсу и по кривизне.
Почему столько внимания уделяется стыковке поверхностей и кривых? Дело в том, что основное занятие моделлера, использующего сплайновые инструменты, это сшивание и подгонка краев поверхностей. Так как NURBS-поверхности не могут быть произвольно объединены в один объект (мы поговорим об этом далее), то, как правило, приходится собирать модель из лоскутов, гладко прилегающих друг к другу.
Рассмотрим теперь все эти понятия и названия на примере работы с кривыми. А про пугающую параметризацию поговорим чуть позже.
Создание кривых. Практические инструменты и методы
Можно выделить несколько способов создания кривых в MAYA.
