
Рис. 14.6. Эффект адаптивного аналитического сглаживания на чайниках разных размеров. Для сравнения верхние чайники нарисованы без сглаживания. При рисовании нижних чайников использовался описанный шейдер. Сглаживание краев полосок выглядит хорошо в обоих масштабах. Но на краях объектов дефекты изображения все же видны
Метод работает хорошо, пока ширина фильтра не превысит частоту, что и происходит на северном полюсе сферы. Полоски возле полюса получаются намного тоньше одного пиксела, и функция step не может здесь иметь нормальное значение. В таких областях объекта нужно применять интегрирование или ограничение частоты (оба метода будут описаны в дальнейшем).
14.4.4. Аналитическое интегрирование
Средневзвешенное значение функции в заданном интервале называется свёрткой. Исходные данные для вычисления средневзвешенного значения называются ядро свёртки или свёрточный фильтр. В некоторых случаях можно определить свёртку функции заранее и в дальнейшем использовать для семплинга результат этих вычислений, а не функцию-оригинал. Свёртку в вычислениях можно выполнять через определенный промежуток, как если бы свёртка входной функции происходила через прямоугольный фильтр. Этот способ далек от идеала, но прост, в нем легко выполнять вычисления, и зачастую этого достаточно для улучшения качества изображения.
Описанный метод называется методом зонального семплинга', в нем некоторые вычисления зависят от того, в какой зоне заданного объекта находятся текущие координаты. Если этот метод будет использоваться применительно к изображению, приведенному на рис. 14.2, то для каждого конкретного пиксела будут вычислены более точные значения.
В книге [2] рассказывается, как выполнять аналитическое сглаживание периодической функции step, иногда этот процесс называют серией импульсов. Используем этот метод для сглаживания кирпичной стенки в процедурном шейдере, описанном в главе 6 этой книги. В шейдере функция step используется для того, чтобы рисунок был периодическим. Функция, вычисляющая рисунок кирпичей в горизонтальном направлении, изображена на рис. 14.7. Отточки 0 до точки BrickPct .х (ширина кирпича) значение функции равно 1,0. В точке BrickPct .х находится край с бесконечным наклоном функции к 0. В точке 1 функция поднимается обратно в 1,0, и все повторяется для следующих кирпичей.
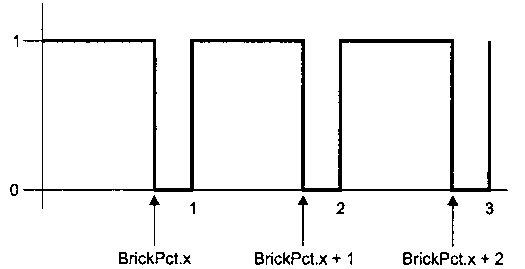
Рис. 14.7. Периодическая функция step (серия импульсов), определяющая горизонтальный компонент процедурной текстуры для кирпичной стены
Для сглаживания этой функции вычисляется ее интегральное значение. В сложных областях ширина фильтра, вычисляемая функцией fwi dth, будет соответствовать нескольким таким импульсам. Выполнив семплинг интегрального значения функции, получим средневзвешенное значение без высоких частот.
Интегральное значение данной функции показано на рис. 14.8. От точки 0 до точки Bri ckPct. х значение функции равно 1,0, так что крутизна функции 1,0. От точки Bri ckPct. х до точки 1 функция имеет значение 0, и теперь интегральное значение постоянное. В точке 1 функция возвращается обратно в 1,0, так что интеграл увеличивается до тех пор, пока функция не достигнет значения Bri ckPct. х + 1. В этой точке значение крутизны меняется до 0, потом все повторяется сначала.
