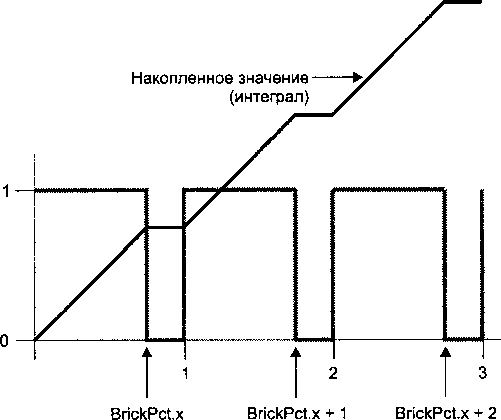
Рис. 14.8. Периодическая функция step (серия импульсов) и ее интегральное значение Для сглаживания нужно определять интегральное значение вне области фильтра. При этом проверяется значение на краях фильтра, и из него вычитаются два значения. Интегральное значение этой функции состоит из двух частей: суммы областей всех импульсов перед краем и области, включающей часть импульса на краю.
Для процедурного шейдера кирпичной стенки переменная position.x принята за основу для функции импульсов в горизонтальном направлении. Количество полных импульсов будет равно f 1 oor (posi ti on. х). Так как высота каждого импульса 1.0, область каждого полного импульса будет Bri ckPct. х. Перемножив эти два значения, получаем область для всех полных импульсов. Край может располагаться в той части функции, где ее значение 1, или в той части, где значение 0. Это можно выяснить, вычислив разность f ract (posi ti on. x) - (1.0 - Bri ckPct. x). Если результат такого вычитания меньше нуля, то точка находится там, где значение функции равно 0, и больше ничего вычислять не требуется. Но если значение больше нуля, точка находится там, где значение функции равно 1,0. Так как высота импульса равна 1,0, область такого «частичного» импульса будет fract (posi tion. х) - (1.0 -BrickPct.x). Вторая часть интегрального значения - выражение max(fract(posi -tion.x) - (1.0 - BrickPct.x), 0.0).
Вычисленное значение можно использовать для горизонтальных и вертикальных компонентов процедурного шаблона кирпичной стенки. Так как приложение знает ширину и высоту кирпичей (Bri ckPct. х и Bri ckPct .у), выражение 1.0- Bri ckPct. х and 1.0 - Bri ckPct. у легко вычислить и передать полученное значение во фрагментный шейдер, что избавит от необходимости рассчитывать его для каждого фрагмента отдельно. Так как выражение будет вычисляться два раза с разными аргументами, удобно определить его как макрос или функцию:
#define Integral(х. p. notp) ((f1оог(х)*(р)) + max(fract(x)-(notp). 0.0))
Параметр р содержит значение части импульса (при значении функции 1,0), а параметр notp содержит значение, не являющееся частью импульса (при значении функции 0). С помощью этого макроса можно написать код для вычисления интегрального значения по всей ширине фильтра: vec2 fw. useBrick;
fw = fwidth(position);
useBrick = (Integral(position + fw. BrickPct, MortarPct) -Integral(position. BrickPct. MortarPct)) / fw: Результат делится на площадь фильтра (в данном случае имеется в виду прямоугольный блок), чтобы получить среднее значение функции в выбранном промежутке.
14.4.5. Фрагментный шейдер кирпичной стенки со сглаживанием
Попробуем заставить описанную процедуру работать. Простая технология семплинга, использованная в примере в главе 6, заменяется аналитической интеграцией. Окончательный шейдер приведен в листинге 14.2. Разница между результатами работы шейдера без сглаживания и шейдера со сглаживанием показана на цветном рис. 25.
Листинг 14.2. Исходный код фрагментного шейдера кирпичной стенки со сглаживанием
uniform vec3 BrickColor, MortarColor: uniform vec2 BrickSize: uniform vec2 BrickPct: uniform vec2 MortarPct;
