float square = smoothstep(0.4. 0.6. triangle):
14.4.3. Адаптивный аналитический предварительный отбор
Описанный в предыдущем подразделе способ сглаживания дает приемлемые результаты не во всех областях сферы. Размер фильтра сглаживания (0,2) определен как параметр. Но при постоянном размере экрана этот параметр не изменяется, а текстурная координата s меняется слишком быстро возле полюсов и слишком медленно - на экваторе. Из-за применения фильтра фиксированной ширины размывка затрагивает несколько пикселов на экваторе, но совсем не видна на полюсах. Нужно найти способ определять размер фильтра сглаживания в зависимости от координат на сфере, чтобы рисунок выглядел лучше. Для этого требуется знать, с какой скоростью должна меняться функция при изменении экранных координат.
К счастью, в языке шейдеров OpenGL есть встроенная функция скорости изменения (производная) любого параметра пространства. Функция dFdx определяет скорость изменения в направлении х, а функция dFdy - скорость изменения в направлении г/. Так как эти функции работают с экранными координатами, они доступны только из фрагментного шейдера. С их помощью можно вычислить вектор-градиент нужных координат.
Два метода вычисления градиента сравниваются на рис. 14.5. Как можно заметить, существует небольшое видимое различие результата. Так как значение градиента слишком маленькое для функции этого объекта, значения были масштабированы.
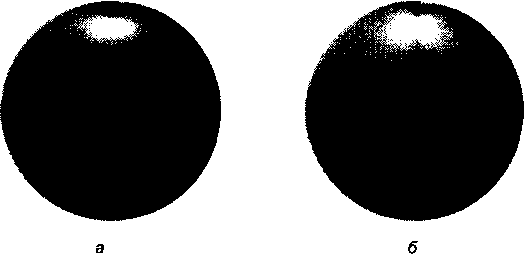
Рис. 14.5. Визуализация градиента: а - модуль вектора градиента используется как значение интенсивности цвета; б- градиент вычислен приближенно (реальные значения градиента масштабированы)1
Чтобы вычислить фактический градиент для varying-переменной V во фрагментном шейдере, используем следующий код: float width = length(vec2 (dFdx(V). dFdy(V))): Вычислим более приблизительное значение, но быстрее:
float width = fwi dth(V): Ширина фильтра затем передается в функцию smoothstep таким образом: float edge = width * 32.0;
float square = smoothstep(0.5 - edge. 0.5 + edge, triangle): Фрагментный шейдер, выполняющий все это, приведен в листинге 14.1.
Листинг 14.1. Фрагментный шейдер для адаптивного аналитического сглаживания
varying float V: // произвольное число
varying float Lightlntensity:
uniform float Frequency; // частота полосок равно б void main (void)
{
float sawtooth = fract(V * Frequency); float triangle = abs(2.0 * sawtooth - 1.0): float dp = length(vec2 (dFdx(V), dFdy(V))): float edge = dp * Frequency * 2.0:
float square = smoothstep(0.5 - edge. 0.5 + edge, triangle); gl_FragColor = vec4 (vec3 (square). 1.0):
}
При масштабировании частоты текстуры соответственно должна увеличиваться ширина фильтра. Вычисленное значение функции записывается в красный, зеленый и синий компоненты вектора типа vec3 и используется в качестве цвета фрагмента. Результат применения метода показан на рис. 14.4, в, размытость более равномерно распределена по сфере. Затем проводятся несложные вычисления освещения, и окончательное изображение накладывается на чайник (рис. 14.6).
