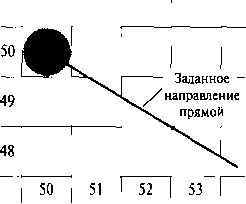
Рис. 3.9. Участок дисплея, на котором изображен отрезок прямой с отрицательным тангенсом угла наклона, начинающийся в пикселе, расположенном в столбце 50 и строке развертки 50
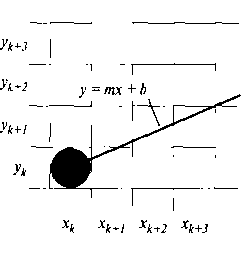
Рис. 3.10. Часть экрана с пикселем в столбце Хк и строке развертки Ук, который будет изображаться в качестве продолжения прямолинейного отрезка с наклоном 0 < гга < 1
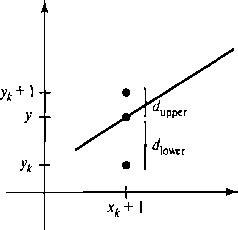
Рис. 3.11. Расстояния по вертикали между положениями пикселей и координатой прямой у в точке выборки х*. + 1
Реализация алгоритма построения прямой линии Брезенхема для тангенса угла наклона в диапазоне 0 < т < 1 приведена в следующей процедуре. Здесь вводятся координаты концов отрезка, а пиксели отображаются от левого конца до правого.
♦include <stdlib.h>
♦include <math.h>
/* Процедура построения отрезка (Брезенхема) для |т| <1,0. */ void lineBres (int х0, int у0, int xEnd, int yEnd)
{
int dx = fabs (xEnd - xO), dy = fabs(yEnd - yO); int p = 2 * dy - dx;
int twoDy = 2 * dy, twoDyMinusDx = 2 * (dy - dx); int x, y;
/* Определяется, какой конец принять в качестве начального
* положения.
*/
if (хО > xEnd) { х = xEnd; у = yEnd; xEnd = хО;
}
else {
х = хО; у = уО;
}
setPixel (х, у);
while (х < xEnd) { х++;
if (Р < 0)
р += twoDy; else {
У++; р += twoDyMinusDx;} setPixel (х, у);
}
}
Алгоритм Брезенхема можно обобщить для прямых линий с произвольным тангенсом угла наклона, рассмотрев симметрию различных октантов и квадрантов плоскости ху. Для прямой с положительным тангенсом угла наклона, превышающим 1,0, роли координат х и у меняются местами. Это означает, что в направлении координаты у делаются единичные шаги, и при этом последовательно вычисляются значения координаты х, ближайшие к направлению прямой. Кроме того, программу можно изменить таким образом, чтобы построение прямой начиналось с другого конца.
ИЗОБРАЖЕНИЕ ЛОМАНЫХ ЛИНИЙ
Для процедуры построения ломаных линий следует гг - 1 раз вызвать процедуру построения прямой линии, в результате чего изображаются прямые линий, соединенные в п точках. При каждом последующем вызове функции сообщается пара наборов координат, необходимых для построения следующего отрезка прямой, причем первой точкой в каждой паре является последняя точка предыдущего отрезка. После того как в буфер кадра заносится код цвета пикселей, составляющих первый отрезок, обрабатывается следующий, начиная с пикселя, идущего после первого конца этого отрезка. Таким образом можно избежать дублирующегося присвоения точкам - концам отрезка кода цвета. Более подробно способы защиты от наложения изображаемых объектов рассмотрены в разделе 3.13.
ПАРАЛЛЕЛЬНЫЕ АЛГОРИТМЫ ПОСТРОЕНИЯ ПРЯМЫХ
В обсуждавшихся выше алгоритмах построения прямых линий положения пикселей определяются последовательно. Параллельная обработка позволяет одновременно рассчитывать положения нескольких пикселей на прямой, распределяя вычисления между различными доступными процессорами. Одним из способов решения задачи распределения является модификация существующего последовательного алгоритма, позволяющая воспользоваться преимуществами, которые предлагают несколько процессоров. Кроме того, можно придумать другой алгоритм обработки, когда положения пикселей эффективно вычисляются по параллельной схеме. При создании параллельного алгоритма важным вопросом является равномерное распределение задач по обработке данных среди доступных процессоров.