♦include <math.h>
inline int round (const float a) { return int (a + 0.5); }
void lineDDA (int xO, int yO, int xEnd, int yEnd) int dx = xEnd - xO, dy = yEnd - yO, steps, k; float xlncrement, ylncrement, x = xO, y = yO;
{ if (fabs (dx) > fabs (dy)) steps = fabs (dx); else
steps = fabs (dy); xlncrement = float (dx) / float (steps); ylncrement = float (dy) / float (steps); setPixel (round (x), round (y)); for (k = 0; k < steps; k++){
х += х1псгешепЪ; у += у1псгетеп-Ь;
setPixel (гоипс! (х), гоипс! (у));
}
}
Алгоритм ЦДА - это более быстрый способ вычисления положений пикселей, чем тот, при котором непосредственно используется уравнение (3.1). В нем операция умножения, фигурирующая в уравнении (3.1), исключена за счет использования растровых характеристик, так что при перемещении по прямой и переходе от одного пикселя к другому прибавляются нужные приросты по направлению х или у. Тем не менее, если отрезки достаточно длинные, то из-за накопления ошибок округления при последовательном прибавлении прироста возможно смещение положение пикселя относительно фактического направления прямой. Более того, операции округления и арифметика с плавающей запятой в этой процедуре все еще требуют очень больших затрат времени. Выполнение алгоритма ЦДА можно ускорить, разделив приросты т и ^ на целую и дробную части, чтобы все вычисления сводились к операциям с целыми числами. Способ вычисления приростов ~ при целочисленном шаге обсуждается в разделе 4.10, а в следующем разделе рассмотрен более общий подход, который можно применять как к прямым, так и к кривым линиям.
АЛГОРИТМ ПОСТРОЕНИЯ ПРЯМЫХ ЛИНИЙ БРЕЗЕНХЕМА
В этом разделе рассмотрен точный и эффективный растровый алгоритм создания прямых линий, разработанный Брезенхемом (ВгевепЬат), в котором вычисляются только целочисленные значения приростов. Кроме того, алгоритм построения прямых Бре-зенхема можно адаптировать для изображения окружностей и других кривых. На рис. 3.8 и 3.9 показаны части экрана дисплея, в которых рисуются прямолинейные отрезки. По вертикальной оси откладывается номер строки развертки, а по горизонтальной - номер столбца пикселей. В этих примерах по координате х берется единичный интервал, и на каждом шаге выборки необходимо определить, какое из двух возможных положений пикселей ближе к прямой. Начиная с левого конца отрезка, показанного на рис. 3.8, нам нужно для каждой последующей точки выборки решить, изображать пиксель с координатами (11, 11) или пиксель с координатами (11, 12). Аналогично на рис. 3.9 показано направление прямолинейного отрезка, левый конец которого находится в пикселе с координатами (50, 50). Здесь нужно выбрать координаты следующего пикселя: (51, 50) или (51, 49). В алгоритме построения прямой линий Брезенхема для этого проверяется знак целочисленного параметра, значение которого пропорционально разности между расстояниями по вертикали от положений этих двух пикселей до действительного направления прямой.
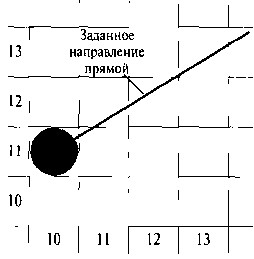
Рис. 3.8. Участок дисплея, на котором изображен отрезок прямой с началом в пикселе, находящемся в столбце 10 и в строке развертки 11
