ЗАПИСЬ ЗНАЧЕНИЙ В БУФЕР КАДРОВ
Последним этапом процедуры изображения прямолинейных отрезков и других объектов является запись кодов цвета в буфер кадра. Поскольку алгоритмы преобразования стандартов развертки выдают координаты пикселей в последовательных единичных интервалах, для эффективного обращения к буферу кадров на каждом шаге процесса преобразования стандартов развертки также можно использовать операции приращения.
Реализация этих процедур зависит от возможностей конкретной системы и проектных требований программного пакета. Для систем, которые могут изображать каждый пиксель с несколькими значениями интенсивности, вычисление адреса из буфера кадра, кроме определения положения пикселя на экране, включают еще и вычисление ширины пикселя (количества битов).
ФУНКЦИИ КРИВЫХ В OpenGL
В корневую библиотеку OpenGL не включены в качестве функций-примитивов функции создания таких кривых основных типов, как окружности или эллипсы. Однако в этой библиотеке есть функции для изображения сплайнов Безье, представляющих собой полиномы, которые задаются набором дискретных точек. В библиотеке OpenGL Utility (GLU) есть процедуры для создания трехмерных поверхностей второго порядка, таких как сферы и цилиндры, а также функции для построения рациональных би-сплайнов, т.е. сплайнов, включающих более простые кривые Безье. С помощью рациональных би-сплайнов можно изображать окружности, эллипсы и другие двухмерные поверхности второго порядка. Кроме того, в пакете OpenGL Utility Toolkit (GLUT) есть процедуры, с помощью которых можно изображать такие трехмерные поверхности второго порядка, как сферы и конусы, а также некоторые другие фигуры. Однако все эти стандартные процедуры намного сложнее, чем те основные примитивы, с которыми мы познакомились в этой главе, поэтому обсуждение этой группы функций мы отложим до главы 8.
Еще один способ создания изображения простой кривой - аппроксимировать ее с помощью ломаной линии. Нужно всего лишь задать набор точек, расположенных на этой кривой, а затем соединить эти точки прямолинейными отрезками. Чем из большего количества отрезков будет состоять ломаная линия, тем более гладкой будет выглядеть кривая. В качестве примера на рис. 3.15 показаны различные изображения ломаных линий, с помощью которых можно аппроксимировать сегмент окружности.
Третий способ - это написать собственную функцию для построения кривой, основанную на алгоритмах, рассмотренных в следующих разделах. Далее подробно описываются эффективные методы построения окружности и эллипса, а затем внимание уделяется процедурам изображения других конических сечений, полиномов и сплайнов.
АЛГОРИТМЫ ПОСТРОЕНИЯ ОКРУЖНОСТЕЙ
Поскольку окружность - это элемент, который часто используется в рисунках и графиках, во многие графические пакеты включена процедура изображения либо полных окружностей, либо различных дуг. Кроме того, иногда в графической библиотеке можно найти функции изображения различных типов кривых, включая окружности и эллипсы.
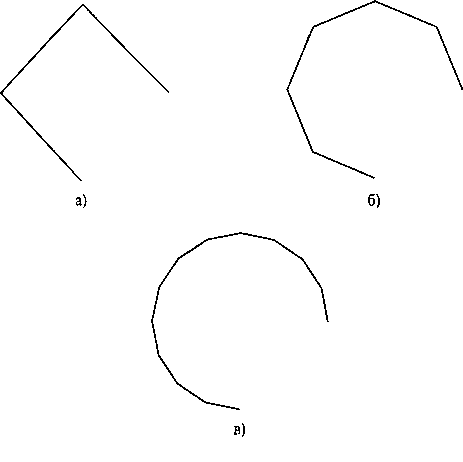
Рис. 3.15. Дуга окружности, аппроксимированная с помощью трех (панель а), шести (панель б) и двенадцати отрезков прямой (панель в)
