При применении методов покрытия клетками вначале определяются координатные границы объекта, затем объект делится на несколько маленьких клеток с использованием данных масштабных коэффициентов. Число клеток п, необходимое для покрытия объекта, называется размером в клетках (box dimension), и п связано с фрактальной размерностью D. Статистически самоподобные объекты с одним

Рис. 8.69. Покрытие квадратиками объекта неправильной формы масштабным коэффициентом в можно покрыть квадратами или кубами. Затем подсчитывается число п покрывающих клеток и с помощью уравнения (8.107) оценивается фрактальная размерность. Самоаффинные объекты покрываются не квадратными, а прямоугольными клетками, поскольку в разных направлениях используются различные масштабные коэффициенты. В этом случае фрактальная размерность оценивается с использованием числа клеток п и параметров аффинного преобразования.
Фрактальная размерность объекта всегда больше соответствующей евклидовой размерности (или топологической размерности), которая является просто наименьшим числом параметров, необходимых для задания объекта. Евклидова кривая одномерна, поскольку точку на ней можно определить одним параметром и. Евклидова поверхность двухмерна, и на ней используются параметры поверхности и иг/. Наконец, евклидово тело, которое требует три параметра для задания всех координат, является трехмерным.
ГЕОМЕТРИЧЕСКОЕ ПОСТРОЕНИЕ ДЕТЕРМИНИРОВАННЫХ САМОПОДОБНЫХ ФРАКТАЛОВ
Чтобы геометрически построить детерминированный (неслучайный) самоподобный фрактал, нужно начать с данной геометрической формы, называемой инициатором, Подчасти инициатора затем заменяются шаблоном, именуемым генератором.
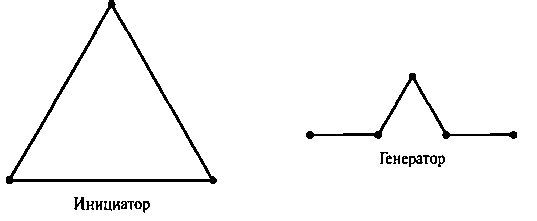
Рис. 8.70. Инициатор и генератор кривой Коха
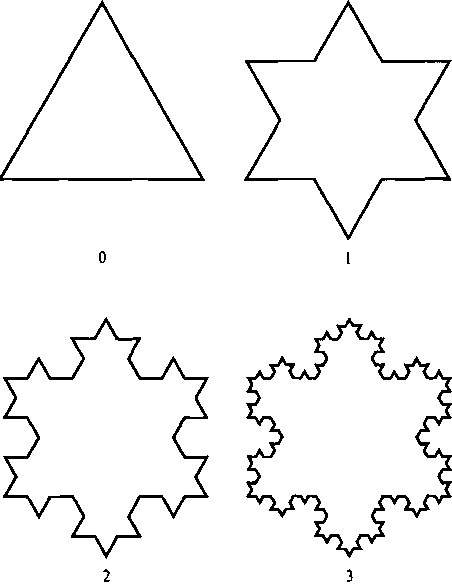
Рис. 8.71. Первые три итерации процесса генерации кривой Коха МЕТОДЫ ПОСТРОЕНИЯ АФФИННЫХ ФРАКТАПОВ
Высоко реалистичные представления местности и других природных объектов можно получить с использованием аффинных фрактальных методов, моделирующих элементы объекта фрактальным броуновским движением. Это является расширением стандартного броуновского движения, разновидности “случайного блуждания”, которое описывает неопределенное зигзагообразное движение частиц в газе или другой текучей среде. На рис. 8.85 иллюстрируется траектория случайного блуждания в плоскости ху. Начиная с данного положения в случайном направлении генерируется прямой отрезок случайной длины. Затем из конца этой первой линии строится другой случайный отрезок, и данный процесс продолжается заданное число раз. Фрактальное броуновское движение получается прибавлением дополнительного параметра к статистическому распределению, описывающему броуновское движение. Данный дополнительный параметр задает фрактальную размерность траектории “движения”.
Для моделирования фрактальной кривой можно использовать одну фрактальную броуновскую траекторию. Имея двухмерный массив случайных дробных броуновских возвышений над сеткой “нулевой плоскости”, можно смоделировать по-
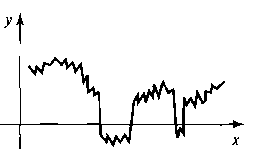
Рис. 8.85. Пример броуновского движения (случайного блуждания) на плоскости ху
