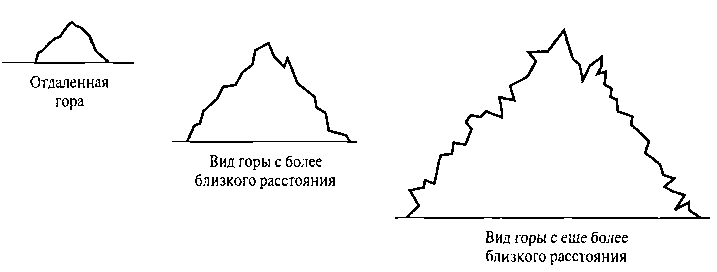
Рис. 8.67. Зазубренный вид контура горы при различных уровнях увеличения широко применяются во многих областях для описания и объяснения особенностей природных явлений. В компьютерной графике фрактальные методы используются для генерации изображений естественных объектов и визуализации различных математических и физических систем.
Фрактальный объект имеет две базовые характеристики: бесконечное число деталей в любой точке и определенное самоподобие частей объекта и общего изображения объекта. Свойство самоподобия объекта может принимать различные формы в зависимости от выбранного представления фрактала. Фрактальный объект описывается процедурой, которая задает повторяющуюся операцию, проявляющую детали подчастей объекта. Природные объекты представляются процедурами, которые теоретически повторяются бесконечное число раз. Разумеется, графические изображения природных объектов строятся за конечное число шагов.
Если увеличивать масштаб непрерывной евклидовой формы (все равно, насколько сложной), со временем укрупненное изображение сгладится. Однако, если увеличивать масштаб фрактального объекта, будет видно все больше и больше деталей без заметного сглаживания внешнего вида объекта. Контур горы на фоне неба будет иметь все ту же зазубренную форму при наблюдении со все более близкого расстояния (рис. 8.67). При приближении к горе становятся видимыми детали отдельных выступов скал и валунов. Если подойти еще ближе, станут видны сначала скалы, затем камни, затем песчинки. С каждым шагом контур становится все более искривленным и изломанным. Если взять песчинки и положить их под микроскоп, можно увидеть, что данная детализация продолжается до молекулярного уровня. Подобные формы описывают побережья и края растений и облаков.
Чтобы получить увеличенное изображение фрактала, можно выбрать участок фрактала и отобразить его в области наблюдения такого же размера, что и исходная, вмещающая весь объект. Затем для этой части объекта вызывается процедура построения фрактала, и при этом уровне увеличения на экране видно большее число дета лей. Если повторять этот процесс, будет отображаться все больше и больше деталей объекта. Поскольку процедурам построения присуща бесконечная детализация, фрактальный объект не имеет определенного размера. Отметим, однако, что при введении в описание объекта большего числа деталей, размеры увеличиваются бесконечно, но координатные границы объекта не выходят из конечной области пространства.
Величину изменения детализации объекта можно охарактеризовать числом, именуемым размерностью фрактала. В отличие от евклидовых размеров это число не обязательно является целым.
Фрактальные методы доказали свою полезность при моделировании огромного множества природных явлений. В графических приложениях фрактальные представления используются для моделирования рельефа местности, облаков, воды, деревьев и другой растительной жизни, перьев, меха и различных поверхностных текстур, а иногда - для получения интересных узоров. В других дисциплинах фрактальные узоры применяются в построении распределения звезд, островов на реке и кратеров на Луне; колебании курсов на фондовой бирже; музыке; транспортном потоке; износе городского имущества; моделировании границ областей сходимости в методах численного анализа.
