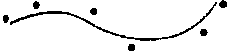
Рис. 8.15. Набор из шести контрольных точек, аппроксимированных кусочно-непрерывными полиномиальными участками Сплайны используются для разработки кривых и поверхностей, для оцифровки рисунков и для задания путей анимации объектов или положений камеры на сцене. Типичные сферы применения автоматизированного проектирования с использованием сплайнов включают разработку кузовов автомобиля, поверхностей самолетов и космических кораблей, корпусов кораблей и бытовых электроприборов.
ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ СПЛАЙНАМИ
Сплайновая кривая задается через набор координат точек, именуемых контрольными, которые указывают общую форму кривой. Затем по данным точкам одним из двух способов подбирается кусочно-непрерывная параметрическая полиномиальная функция. Если полиномиальные участки соединяют все контрольные точки, как показано на рис. 8.14, получающаяся кривая называется интерполяцией набора контрольных точек. С другой стороны, если генерируемая полиномиальная кривая строится так, что некоторые или все контрольные точки не лежат на пути кривой, эта кривая называется аппроксимацией набора контрольных точек (рис. 8.15). Подобные методы используются для построения интерполяций или аппроксимаций сплайновых поверхностей.
Методы интерполяции широко используются для оцифровки рисунков или задания путей анимации. Методы аппроксимации применяются в основном в средствах Проектирования для создания форм объектов. На рис. 8.16, например, показана аппроксимирующая сплайновая поверхность в некотором пакете проектирования. Контрольные точки над поверхностью соединяются прямыми отрезками.
Сплайновая кривая или поверхность определяется, модифицируется и используется путем действий с контрольными точками. Интерактивно выбирая положения контрольных точек в пространстве, разработчик может задавать первоначальную форму. После того как для данного набора контрольных точек на экране отображено полиномиальное представление, разработчик может изменить положения некоторых или Всех контрольных точек, подбирая таким образом структуру формы объекта. Наконец, геометрические преобразования (трансляция, вращение и масштабирование) приме-

Рис. 8.16. Аппроксимирующая онлайновая поверхность в приложении автоматизированного проектирования автомобилей. Контуры поверхности представлены полиномиальными фрагментами кривых, а контрольные точки поверхности соединяются прямыми отрезками (перепечатано с разрешения Evans & Sutherland)
няются к объектам также через преобразование контрольных точек. Кроме того, пакеты автоматизированного проектирования иногда позволяют вводить дополнительные контрольные точки, чтобы помочь разработчику получить требуемую форму объекта.
Набор контрольных точек формирует границу области пространства, называемую выпуклой оболочкой. Чтобы представить себе форму выпуклой оболочки для двухмерной кривой, подумайте о резиновой ленте, которая так натягивается на положения контрольных точек, что каждая контрольная точка находится либо на периметре этой границы, либо внутри него (рис. 8.17). Таким образом, выпуклая оболочка двухмерной сплайновой кривой является выпуклым многоугольником. В трехмерном пространстве выпуклая оболочка набора сплайновых кривых формирует выпуклый многогранник. Вообще, выпуклые оболочки позволяют отклонять кривую или поверхность от области пространства вблизи контрольных точек. В большинстве случаев сплайн ограничивается его выпуклой оболочкой, а это гарантирует, что форма объекта следует за контрольными точками без ложных осцилляций. Кроме того, выпуклая оболочка - это мера координатных границ заданной кривой или поверхности, так что ее удобно использовать в процедурах поворота и изменения точки наблюдения.
