glutDisplayFunc (wireQuadSurfs) ; glutReshapeFunc (winReshapeFcn);
glutMainLoop ( );
}
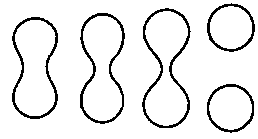
Рис. 8.9. Молекулярные связи. При удалении двух молекул друг от друга поверхности растягиваются, обрываются и наконец сжимаются в сферы
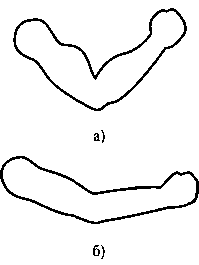
Рис. 8.10. “Каплевидные” мускулы руки человека КАПЛЕВИДНЫЕ ОБЪЕКТЫ
На настоящее время в приложениях компьютерной графики разработано множество технологий моделирования нежестких объектов, а методы отображения характеристик таких материалов, как одежда и резина, обсуждаются в разделе 8.26. Однако такие объекты, как молекулярные структуры, жидкости и капли воды, плавящиеся объекты и мускулы людей и животных, имеют определенную степень текучести. Они меняют свои поверхностные характеристики при определенных движениях, или когда в окрестности находятся другие объекты, также для них характерны криволинейные поверхности, которые нельзя просто представить с использованием стандартных форм. В совокупности все такие объекты называются каплевидными (blobby objects).
Форму отдельных молекул, например, можно считать сферической, но она меняется при приближении одной молекулы к другой. Это объясняется тем, что плотность электронного облака искажается присутствием других молекул, так что возникают краевые эффекты. На рис. 8.9 иллюстрируется растяжение, обрыв и сжимание молекулярных форм при удалении двух молекул друг от друга. Подобные свойства проявляют мускулы человеческой руки, показанные на рис. 8.10. Отметим, что данные характеристики нельзя адекватно описать просто с помощью сферических или эллиптических форм.
Было разработано несколько моделей для представления каплевидных объектов как функций распределения в области пространства. Обычно формы поверхностей описываются так, что объем объекта остается постоянным при любых движениях или взаимодействиях. Один метод моделирования каплевидных объектов - использовать
СП.ПАЙНОВЫЕ ПРЕДСТАВЛЕНИЯ
В черчении сплайном называется гибкая полоска, используемая для получения гладкой кривой, проходящей по набору заданных точек. Чтобы удержать полоску на чертежном столе при проведении кривой, вдоль нее распределяется несколько небольших гирек. Термином онлайновая кривая изначально называлась кривая, нарисованная указанным выше способом. Математически эту кривую можно описать кусочно-гладкой кубической полиномиальной функцией, первая и вторая производная которой непрерывны на различных участках кривой. В компьютерной графике сплайновой кривой сейчас называют любую составную кривую, сформированную полиномиальными участками, удовлетворяющими заданным условиям непрерывности на границах участков. Онлайновую поверхность можно описать двумя наборами ортогональных сплайновых кривых. Существует несколько различных типов определений сплайнов, используемых в приложениях компьютерной графики. Каждая отдельная спецификация просто связана с определенным типом полиномов с конкретными предопределенными граничными условиями.
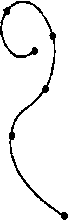
Рис. 8.14. Набор из шести контрольных точек, интерполированных кусочно-гладкой непрерывной полиномиальной кривой
